2005 Summer Institute on String Summer School on String

1
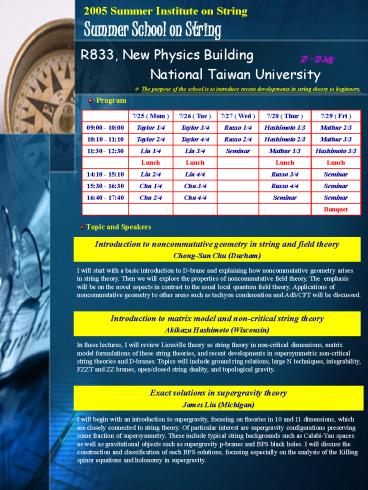
2005 Summer Institute on StringSummer School on
String

• R833, New Physics Building
• National Taiwan University

25 29 July
The purpose of the school is to introduce
recent developments in string theory to
beginners.

• Program

7/25 ( Mom ) 7/26 ( Tue ) 7/27 ( Wed ) 7/28 ( Thur ) 7/29 ( Fri )
0900 - 1000 Taylor 1/4 Taylor 3/4 Russo 1/4 Hashimoto 1/3 Mathur 2/3
1010 - 1110 Taylor 2/4 Taylor 4/4 Russo 2/4 Hashimoto 2/3 Mathur 3/3
1130 - 1230 Liu 1/4 Liu 3/4 Seminar Mathur 1/3 Hashimoto 3/3
Lunch Lunch Lunch Lunch
1410 - 1510 Liu 2/4 Liu 4/4 Russo 3/4 Seminar
1530 - 1630 Chu 1/4 Chu 3/4 Russo 4/4 Seminar
1640 - 1740 Chu 2/4 Chu 4/4 Seminar Seminar
Banquet

• Topic and Speakers

Introduction to noncommutative geometry in string
and field theory Chong-Sun Chu (Durham)
I will start with a basic introduction to D-brane
and explaining how noncommutative geometry arises
in string theory. Then we will explore the
properties of noncommutative field theory. The
emphasis will be on the novel aspects in contrast
to the usual local quantum field theory.
Applications of noncommutative geometry to other
areas such as tachyon condensation and AdS/CFT
will be discussed.
Introduction to matrix model and non-critical
string theory Akikazu Hashimoto (Wisconsin)
In these lectures, I will review Liouville theory
as string theory in non-critical dimensions,
matrix model formulations of these string
theories, and recent developments in
supersymmetric non-critical string theories and
D-branes. Topics will include ground ring
relations, large N techniques, integrability,
FZZT and ZZ branes, open/closed string duality,
and topological gravity.
Exact solutions in supergravity theory James Liu
(Michigan)
I will begin with an introduction to
supergravity, focusing on