Introducci - PowerPoint PPT Presentation
Title: Introducci
1
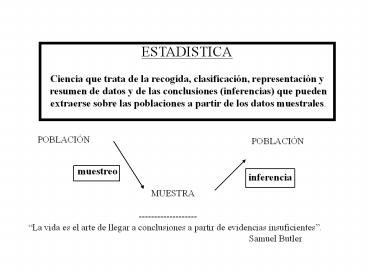
ESTADISTICA Ciencia que trata de la recogida,
clasificación, representación y resumen de datos
y de las conclusiones (inferencias) que pueden
extraerse sobre las poblaciones a partir de los
datos muestrales.
POBLACIÓN
POBLACIÓN
muestreo
inferencia
MUESTRA
------------------- La vida es el arte de
llegar a conclusiones a partir de evidencias
insuficientes. Samuel Butler
2
LO QUE SE HACE EN ESTADISTICA
- Describir (DESCRIPTIVA) centro, dispersión,
forma, simetría, curtosis. - Inferir sobre la población a partir del
conocimiento de la muestra (INFERENCIAL) - - Estimación de parámetros.
- - Contrastes (tests) sobre los parámetros de
una distribución. - - Contrastes (tests) sobre la forma general de
la distribución. - - Comparaciones entre parámetros de una
variable en dos o más poblaciones. - - Relaciones entre dos variables en una
población. - . Inferir o buscar estructuras en una o varias
poblaciones a partir del conocimiento de varias
variables de la muestra (MULTIVARIANTE).
3
Tipos de VARIABLES -Dicotómicas (dos
modalidades) Nominales-
Cualitativas Ordinales Discretas -
Cuantitativas Continuas
4
Cualitativas Sus modalidades no necesitan
números para ser expresadas. Nominales Sus
modalidades no tienen un orden
natural. Ordinales Sus modalidades tienen un
orden natural. Cuantitativas Sus valores
necesitan números para ser expresados. Discretas
Sus valores son aislados (entre dos
consecutivos no hay otro). Continuas Sus
valores son continuos (entre cada dos valores
hay infinitos).
5
Otra clasificación para las variables
cuantitativas Escala de intervalo No tienen
cero absoluto y tiene sentido calcular
diferencias entre sus valores, pero no cocientes.
Escala de razón Tienen cero absoluto y tiene
sentido calcular diferencias y cocientes entre
sus valores. Clasificación práctica Por el
número de valores razonablemente posibles de la
variables (si tiene pocos valores se maneja como
discreta y si tiene muchos como continua). El
límite entre pocos y muchos valores posibles
debe establecerse en términos prácticos serán
pocos si existe la posibilidad de comprender
tablas, gráficas e informes sobre los datos si se
enumera de uno en uno cada valor posible, sin
agruparlos en intervalos.
6
CALIDAD ESTADISTICA de las variables
- Dicotómicas (las menos informativas)
- Nominales
- Ordinales con pocas modalidades
- Ordinales con muchas modalidades
- Codificaciones pseudonuméricas
- Discreta con pocos valores
- Discretas con muchos valores
- Continuas con pocos decimales
- Continuas con muchos decimales (las más
informativas)
7
Distribución del grupo sanguíneo de una muestra
de 500 donantes
Grupo sanguíneo Frecuencia absoluta Frecuencia relativa Porcentaje ()
A B AB 0 150 75 25 250 0.30 0.15 0.05 0.50 30 15 5 50
Totales 500 1 100
8
Distribución del número de hermanos de una
muestra de 13 escolares4 3 0 1 0 7
2 0 1 1 5 2 0Datos ordenados0 0
0 0 1 1 1 2 2 3 4 5 7
Nº de hermanos Frecuencia absoluta Frecuencia relativa Porcentaje ()
0 1 2 3 4 5 6 7 4 3 2 1 1 1 0 1 0.308 0.231 0.154 0.077 0.077 0.077 0.000 0.077 30.8 23.1 15.4 7.7 7.7 7.7 0.0 7.7
Totales 13 1 100
9
Distribución del número de hermanos de una
muestra de 13 escolares4 3 0 1 0 7
2 0 1 1 5 2 0Datos ordenados0 0
0 0 1 1 1 2 2 3 4 5 7
Desviaciones (la media es 2.00) -2 -2 -2 -2 -1 -1 -1 0 0 1 2 3 5 -2 -2 -2 -2 -1 -1 -1 0 0 1 2 3 5 -2 -2 -2 -2 -1 -1 -1 0 0 1 2 3 5 Suma de desviaciones 0
Desviaciones al cuadrado 4 4 4 4 1 1 1 0 0 1 4 9 25 4 4 4 4 1 1 1 0 0 1 4 9 25 4 4 4 4 1 1 1 0 0 1 4 9 25 Suma de cuadrados de desviaciones 58
VARIANZA 58 / 12 4.833 VARIANZA 58 / 12 4.833 Desviación típica Raíz cuadrada de la varianza 2.20 Coeficiente de variación 2.20 / 2.00 1.100 110.0 Coeficiente de variación 2.20 / 2.00 1.100 110.0
10
Distribución del peso (Kg.) de una muestra de 500
estudiantes
Intervalos de peso (clases) Marcas de clase Frecuencia absoluta Frecuencia relativa Frecuencia relativa acumulada
( - 45) 45 - 50) 50 - 55) 55 - 60) 60 - 65) 65 - 70) 70 - 75) 75 - 80) 80 - 85) 85 - 90) 90 - ) 42.5 47.5 52.5 57.5 62.5 67.5 72.5 77.5 82.5 87.5 92.5 1 3 12 75 103 155 101 29 11 8 2 0.002 0.006 0.024 0.150 0.206 0.310 0.202 0.058 0.022 0.016 0.004 0.002 0.008 0.032 0.182 0.388 0.698 0.900 0.958 0.980 0.996 1.000
Totales 500 1 100
11
- Normas para la construcción de TABLAS y GRAFICAS
- TABLAS
- Deben tener un enunciado que las explique por sí
mismas. - Deben indicar los totales de las columnas.
- Deben indicar las unidades de medida de la/s
variable/s. - Deben tener el mismo número de decimales en los
números de una misma columna. - GRAFICAS
- - DEBEN TENER LONGITUDES o SUPERFICIES
PROPORCIONALES A LAS FRECUENCIAS. - - Deben adecuarse al tipo de variable,
respetando el orden de las modalidades en las
variables ordinales y el lugar que ocupa cada
valor en las variables numéricas. - - En los histogramas, la longitud de los
intervalos debería ser igual en todos. - - En los histogramas, no debe haber huecos entre
los intervalos. - - En los histogramas, el número de intervalos
debería estar entre 5 y 15, dependiendo del
tamaño de la muestra a mayor cantidad de datos,
mayor número de clases.
12
Normas para la construcción de TABLAS y
GRAFICAS CAUSAS MAS FRECUENTES DE LAS GRAFICAS
INADECUADAS O ERRONEAS - RUPTURA DE LA
PROPORCIONALIDAD ENTRE LONGITUDES o SUPERFICIES Y
FRECUENCIAS. - Porque se tumban los diagramas
de sectores, cambiando el círculo a una elipse.
(ERRONEAS). - Porque se da grosor
tridimensional en cualquier gráfica, creando
sensaciones que hacen perder la dimensionalidad
de la percepción (dos dimensiones, tres
dimensiones?. (INADECUADAS). - Porque se cortan
los ejes, en particular el que refleja las
frecuencias (suele ser el vertical).
(INADECUADAS). - Porque en los histogramas la
longitud de los intervalos no es igual en todos
y se dibujan directamente las frecuencias, no
las densidades de frecuencia. (ERRONEAS). -
Porque en los pictogramas (gráficas con figuras)
se hacen proporcionales a las frecuencias tanto
las bases como las alturas. (ERRONEAS). -
CONFUSION PORQUE SE INTENTA EXPRESAR DEMASIADA
INFORMACION EN UNA SOLA GRAFICA (gráficas
superpuestas). (INADECUADAS).
13
Medidas de POSICION (CUANTILES)
- Definen la situación de los valores con respecto
al conjunto de la distribución. - MEDIANA (Me). El valor que supera (o iguala) al
50 de la distribución. - CUARTILES (Q1 y Q3). Los valores que superan (o
igualan) al 25 y al 75 de la distribución,
respectivamente. - DECILES. Como los cuartiles pero para el 10,
20, 30,......, 90. - PERCENTILES. Como los cuartiles pero para el 1,
2, 3,......, 98, 99.
14
Medidas de CENTRALIZACION, TENDENCIA CENTRAL ó
POSICION CENTRAL
- Dan un resumen de toda la distribución en un solo
valor. - MODA (Mo). La modalidad ó valor más frecuente.
- MEDIANA (Me). El valor que supera (o iguala) al
50 de la distribución y se ve superado (o
igualado) por el otro 50. Es el centro de la
distribución de los datos ordenados, pero sin
tener en cuenta sus valores, sino sólo su orden. - MEDIA ó MEDIA ARITMETICA ( x ). La suma de los
datos dividida entre el número de ellos. Es el
centro de gravedad o equilibrio de los datos,
teniendo en cuenta sus valores.
15
Medidas de DISPERSION
- Miden las diferencias entre los datos.
- RANGO INTERCUARTILICO (R). Es la diferencia entre
los cuartiles ( Q3 Q1 ). - DESVIACION ABSOLUTA MEDIA. Es la media de los
valores absolutos de las desviaciones
(diferencias entre cada dato y la media). - VARIANZA. Es la media de los cuadrados de las
desviaciones. - DESVIACION TIPICA ó DESVIACION STANDARD. Es la
raíz cuadrada de la varianza. - COEFICIENTE DE VARIACION. Es la desviación típica
dividida entre la media, a menudo multiplicada
por 100 y expresada como si fuera un porcentaje
(que no lo es, porque puede ser mayor de 100).
16
- Medidas para la muestra del grupo sanguíneo (n
500) - Medidas de posición NO HAY, porque el grupo
sanguíneo es una característica NOMINAL y no
tiene orden. - Medidas de centralización SOLO LA MODA, que es
el grupo sanguíneo 0 (cero), por ser el más
frecuente. - Medidas de dispersión NO HAY, porque el grupo
sanguíneo es una característica NOMINAL y no
tiene orden.
17
Medidas para la muestra del número de hermanos (n
13) Es una variable discreta, con un n
pequeño. Medidas de posición a partir de
(n1)/2 7º, etc. Mediana 1 (valor
central). Cuartiles Q1 0 Q3
3.5 Deciles y percentiles, no tienen sentido (n
pequeño). Medidas de centralización Moda 0
(el más frecuente). Mediana 1 (valor
central). Media 2.00 (reparto igualitario,
centro de equilibrio). Medidas de dispersión a
partir de la suma, que es 26, y de la suma de
cuadrados, que es 110, de los
datos. Varianza 4.833 Desviación standard
2.20 Coeficiente de variación 109.9 (gran
dispersión).
18
Medidas para la muestra del peso (n 500) Es una
variable continua, con un n grande. Medidas de
posición a partir de n/2 250º, etc.
Intervalo de la mediana 65-70) (valor
aproximado 68.19). Intervalo del primer
cuartil 60-65) (valor aproximado
63.35). Intervalo del tercer cuartil 70-75)
(valor aproximado 73.71). Medidas de
centralización Intervalo de la moda 65-70)
(valor aproximado 67.48). Intervalo de la
mediana 65-70) (valor aproximado
68.19). Media aproximada 66.78 Medidas de
dispersión a partir de la suma aproximada, que
es 33390, y de la suma de cuadrados aproximada,
que es 2256475, de los datos. Varianza
53.489 Desviación standard 7.31 Coeficiente
de variación 11.0 (pequeña dispersión).
19
TEST MAS FRECUENTES PARA UNA VARIABLE
Con 1 muestra Con 2 muestras Con 3 ó más muestras
Para una media NORMAL STUDENT Comparación de dos medias Apareadas Independientes STUDENT STUDENT WELCH Comparación de tres o más medias Apareadas Independientes ANOVA II ANOVA I (BLOQUES)
Comparación de dos medias (test no paramétricos) Apareadas Independientes WILCOXON MANN-WHITNEY Comparación de tres o más medias (test no paramétricos) Apareadas Independientes FRIEDMAN KRUSKAL-WALLIS
Para una proporción EXACTO NORMAL Comparación de dos proporciones Apareadas Independientes MC NEMAR EXACTO de FISHER NORMAL JI-CUADRADO Comparación de tres o más proporciones independientes JI-CUADRADO
20
TEST PARA LA RELACIÓN DE DOS VARIABLES EN UNA
POBLACIÓN
Relación (asociación) entre dos variables CUALITATIVAS Relación (asociación) entre dos variables CUANTITATIVAS
JI-CUADRADO Test para el COEFICIENTE DE CORRELACIÓN (equivalente al test de pendiente nula)
Relación entre una variable CUALITATIVA y otra CUANTITATIVA viene dada por la comparación entre las medias de la cuantitativa de las submuestras determinadas por las modalidades de la cualitativa (ver comparación de dos o de tres o más medias en el esquema anterior). Relación entre una variable CUALITATIVA y otra CUANTITATIVA viene dada por la comparación entre las medias de la cuantitativa de las submuestras determinadas por las modalidades de la cualitativa (ver comparación de dos o de tres o más medias en el esquema anterior).