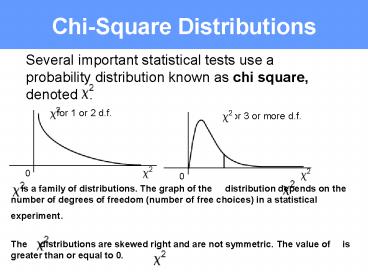
Chi-Square Distributions

1
Chi-Square Distributions
Several important statistical tests use a
probability distribution known as chi square,
denoted .
for 1 or 2 d.f.
for 3 or more d.f.
0
0
is a family of distributions. The graph of
the distribution depends on the number of
degrees of freedom (number of free choices) in a
statistical experiment.
The distributions are skewed right and are
not symmetric. The value of is greater than
or equal to 0.
2
Multinomial Experiments
A multinomial experiment is a probability
experiment in which there are a fixed number of
independent trials and there are more than two
possible outcomes for each trial.

• The probability for each outcome is fixed.
• The sum of the probabilities of all possible
  outcomes is one.

A chi-square goodness-of-fit test is used to test
whether a frequency distribution fits a specific
distribution.
3
Chi-Square Test for Goodness-of-Fit
Example A social service organization claims 50
of all marriages are the first marriage for both
bride and groom, 12 are first for the bride
only, 14 for the groom only and 24 a remarriage
for both.
H0 The distribution of first-time marriages is
50 for both bride and groom, 12 for the bride
only, 14 for the groom only. 24 are
remarriages for both.
H1 The distribution of first-time marriages
differs from the claimed distribution.
4
Goodness-of-Fit Test
Observed frequency, O, is the frequency of the
category found in the sample.
Expected frequency, E, is the calculated
frequency for the category using the specified
distribution. Ei npi
In a survey of 103 married couples, find the E
expected number in each category.
E np
103(.50) 51.50
103(.12) 12.36
103(.14) 14.42
103(.24) 24.72
5
Chi-Square Test
If the observed frequencies are obtained from a
random sample and each expected frequency is at
least 5, the sampling distribution for the
goodness-of-fit test is a chi-square distribution
with k 1 degrees of freedom (where k the
number of categories).
The test statistic is
O observed frequency in each category
E expected frequency in each category
6
A social service organization claims 50 of all
marriages are the first marriage for both bride
and groom, 12 are first for the bride only, 14
for the groom only, and 24 a remarriage for
both. The results of a study of 103 randomly
selected married couples are listed in the table.
Test the distribution claimed by the agency.
Use .
1. Write the null and alternative hypothesis.
H0 The distribution of first-time marriages is
50 for both bride and groom, 12 for the bride
only, 14 for the groom only. 24 are
remarriages for both.
Ha The distribution of first-time marriages
differs from the claimed distribution.
2. State the level of significance.
7
3. Determine the sampling distribution.
A chi-square distribution with 4 1 3 d.f.
4. Find the critical value.
5. Find the rejection region.
2
11.34
0
6. Find the test statistic.
(O E)2
12.25__
0.1296
5.8564
0.5184
0.6755
8
11.34
0
7. Make your decision.
The test statistic 0.6755 does not fall in the
rejection region, so fail to reject H0.
8. Interpret your decision.
The distribution fits the specified distribution
for first-time marriages.