Machine Learning - PowerPoint PPT Presentation
Title:
Machine Learning
Description:
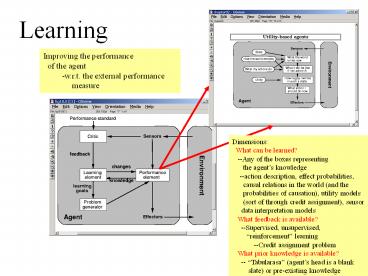
Learning Improving the performance of the agent-w.r.t. the external performance measure Dimensions: What can be learned?--Any of the boxes representing – PowerPoint PPT presentation
Number of Views:1384
Avg rating:3.0/5.0
Title: Machine Learning
1
Learning
Improving the performance of the agent -w.r.t.
the external performance measure
Dimensions What can be learned? --Any of
the boxes representing the agents
knowledge --action description, effect
probabilities, causal relations in the
world (and the probabilities of
causation), utility models (sort of through
credit assignment), sensor data
interpretation models What feedback is
available? --Supervised, unsupervised,
reinforcement learning --Credit
assignment problem What prior knowledge is
available? -- Tabularasa (agents head is
a blank slate) or pre-existing knowledge
2
(No Transcript)
3
Dimensions of Learning
- Representation of the knowledge
- Degree of Guidance
- Supervised
- Teacher provides training examples solutions
- E.g. Classification
- Unsupervised
- No assistance from teacher
- E.g. Clustering Inducing hidden variables
- In-between
- Either feedback is given only for some of the
examples - Semi-supervised Learning
- Or feedback is provided after a sequence of
decision are made - Reinforcement Learning
- Degree of Background Knowledge
- Tabula Rasa
- No background knowledge other than the training
examples - Knowledge-based learning
- Examples are interpreted in the context of
existing knowledge - Knowledge Level vs. Speedup Learning
- If you do have background knowledge, then a
question is whether the learned knowledge is
entailed by the background knowledge or not - (Entailment can be logical or probabilistic)
- If it is entailed, then it is called deductive
learning - If it is not entailed, then it is called
inductive learning
4
Inductive Learning(Classification Learning)
- Given a set of labeled examples
- Find the rule that underlies the labeling
- (so you can use it to predict future unlabeled
examples) - Tabularasa, fully supervised
- Too hard as given.. Need to constrain the space
of rules - Bias Start with a specific form of hypothesis
space - With a given bias, Inductive learning reduces to
winnowing through the hypotheses spacechecking
to see which of them fit the data best
--similar to predicting credit card fraud,
predicting who are likely to respond to junk
mail predicting what items you are likely to
buy
Closely related to Function learning
or curve-fitting (regression)
5
Inductive Learning(Classification Learning)
- Given a set of labeled training examples
- Find the rule that underlies the labeling
- (so you can use it to predict future unlabeled
examples) - Tabula Rasa, fully supervised
- Qns
- How do we test a learner?
- Can learning ever work?
- How do we compare learners?
--similar to predicting credit card fraud,
predicting who are likely to respond to junk
mail predicting what items you are likely to
buy
Closely related to Function learning
or curve-fitting (regression)
6
Inductive Learning(Classification Learning)
- How are learners tested?
- Performance on the test data (not the training
data) - Performance measured in terms of positive
- (when) Can learning work?
- Training and test examples the same?
- Training and test examples have no connection?
- Training and Test examples from the same
distribution
7
Uses different biases in predicting Russels
waiting habbits
Decision Trees --Examples are used to --Learn
topology --Order of questions
K-nearest neighbors
If patronsfull and dayFriday then wait
(0.3/0.7) If waitgt60 and Reservationno then
wait (0.4/0.9)
Association rules --Examples are used to
--Learn support and confidence of
association rules
SVMs
Neural Nets --Examples are used to --Learn
topology --Learn edge weights
Naïve bayes (bayesnet learning) --Examples are
used to --Learn topology --Learn CPTs
8
Inductive Learning(Classification Learning)
- Given a set of labeled examples, and a space of
hypotheses - Find the rule that underlies the labeling
- (so you can use it to predict future unlabeled
examples) - Tabularasa, fully supervised
- Idea
- Loop through all hypotheses
- Rank each hypothesis in terms of its match to
data - Pick the best hypothesis
- Main variations
- Bias the sort of rule are you looking for?
- If you are looking for only conjunctive
hypotheses, there are just 3n - Search
- Greedy search
- Decision tree learner
- Systematic search
- Version space learner
- Iterative search
- Neural net learner
It can be shown that sample complexity of PAC
learning is proportional to 1/e, 1/d AND log H
The main problem is that the space of
hypotheses is too large Given examples described
in terms of n boolean variables There are 2
different hypotheses For 6 features, there are
18,446,744,073,709,551,616 hypotheses
2n
9
A good hypothesis will have fewest false
positives (Fh) and fewest false negatives
(Fh-) Ideally, we want them to be zero Rank(h)
f(Fh, Fh-) --f depends on the domain
by default fSum but can give different
weights to different errors (Cost-based
learning)
False ve The learner classifies the example
as ve, but it is actually -ve
Ranking hypotheses
Medical domain --Higher cost for F- --But
also high cost for F Spam Mailer --Very low
cost for F --higher cost for
F- Terrorist/Criminal Identification --High
cost for F (for the individual) --High cost
for F- (for the society)
H1 Russell waits only in italian restaurants
false ves X10, false ves
X1,X3,X4,X8,X12 H2 Russell waits only in cheap
french restaurants False ves False
ves X1,X3,X4,X6,X8,X12
10
K-Nearest Neighbor
- An unseen instances class is determined by its
nearest neighbor - Or the majority label of its nearest k neighbors
- Real Issue Getting the right distance metric to
decide who are the neighbors - One of the most obvious classification algorithms
- Skips the middle stage and lets the examples be
their own pattern - A variation is to cluster the training examples
and remember the prototypes for each cluster
(reduces the number of things remembered)
11
A classification learning example Predicting when
Rusell will wait for a table
--similar to book preferences, predicting credit
card fraud, predicting when people are likely
to respond to junk mail
12
11/28
Final exam options (vote) Option 1. Take-home
(that will be given after reading day
and will be due ¼
10th) Option 2. In class exam (on 10th)
Option 3. No exam. Rao gets rest, and everybody
gets A
- ?Blog questions
- ?Decision Tree learning
- ?Perceptron learning
13
What is a reasonable goal in designing a learner?
Complexity measured in number of Samples
required to PAC-learn
- (Idea) Learner must classify all new instances
(test cases) correctly always - Any test cases?
- Test cases drawn from the same distribution as
the training cases - Always?
- May be the training samples are not completely
representative of the test samples - So, we go with probably
- Correctly?
- May be impossible if the training data has noise
(the teacher may make mistakes too) - So, we go with approximately
- The goal of a learner then is to produce a
probably approximately correct (PAC) hypothesis,
for a given approximation (error rate) e and
probability d. - When is a learner A better than learner B?
- For the same e,d bounds, A needs fewer trailing
samples than B to reach PAC.
N 1/² ( log 1/ log H)
14
PAC learning
Note This result only holds for finite
hypothesis spaces (e.g. not valid for the space
of line hypotheses!)
N 1/² ( log 1/ log H)
15
Deriving Sample Complexity for PAC Learning
- IDEA We want to compute the probability that a
bad hypothesis (that makes more than ² error on
the test cases) is chosen for being consistent
with the training examples, and constrain it to
be less than - Probability that an hb 2 Hbad is consistent with
a single training example is (1 - ²) (since
error rate of hb gt ²). - This holds ONLY because we assume training and
test instances are drawn with the same
distribution - The probability that it is consistent with all N
training examples is (1-²)N - The probability that at least one bad hypothesis
does this is Hbad (1-²)N H (1-²)N ( since
Hbad H) - We want this probability be less than .
- That is H (1-²)N
- Since (1 - ²) e-² we can have it if H e-²N
or N 1/² (log 1/ log H)
hb
-
hb
-
-
-
-
-
-
-
-
-
-
-
16
Uses different biases in predicting Russels
waiting habbits
Decision Trees --Examples are used to --Learn
topology --Order of questions
K-nearest neighbors
If patronsfull and dayFriday then wait
(0.3/0.7) If waitgt60 and Reservationno then
wait (0.4/0.9)
Association rules --Examples are used to
--Learn support and confidence of
association rules
SVMs
Neural Nets --Examples are used to --Learn
topology --Learn edge weights
Naïve bayes (bayesnet learning) --Examples are
used to --Learn topology --Learn CPTs
17
Inductive Learning(Classification Learning)
- Given a set of labeled examples, and a space of
hypotheses - Find the rule that underlies the labeling
- (so you can use it to predict future unlabeled
examples) - Tabularasa, fully supervised
- Idea
- Loop through all hypotheses
- Rank each hypothesis in terms of its match to
data - Pick the best hypothesis
- Main variations
- Bias the sort of rule are you looking for?
- If you are looking for only conjunctive
hypotheses, there are just 3n - Search
- Greedy search
- Decision tree learner
- Systematic search
- Version space learner
- Iterative search
- Neural net learner
It can be shown that sample complexity of PAC
learning is proportional to 1/e, 1/d AND log H
The main problem is that the space of
hypotheses is too large Given examples described
in terms of n boolean variables There are 2
different hypotheses For 6 features, there are
18,446,744,073,709,551,616 hypotheses
2n
18
Learning Decision Trees---How?
Basic Idea --Pick an attribute --Split
examples in terms of that attribute
--If all examples are ve label Yes.
Terminate --If all examples are ve
label No. Terminate --If some are ve, some
are ve continue splitting
recursively (Special case Decision Stumps If
you dont feel like splitting any further,
return the majority label )
20 Questions AI Style
19
Decision Trees Sample Complexity
- Decision Trees can Represent any boolean function
- ..So PAC-learning decision trees should be
exponentially hard (since there are 22n
hypotheses) - ..however, decision tree learning algorithms use
greedy approaches for learning a good (rather
than the optimal) decision tree - Thus, using greedy rather than exhaustive search
of hypotheses space is another way of keeping
complexity low (at the expense of losing PAC
guarantees)
20
Depending on the order we pick, we can get
smaller or bigger trees
Which tree is better? Why do you think so??
21
Basic Idea --Pick an attribute --Split
examples in terms of that attribute
--If all examples are ve label Yes.
Terminate --If all examples are ve
label No. Terminate --If some are ve, some
are ve continue splitting recursively
--if no attributes left to split?
(label with majority element)
22
The Information Gain Computation
P N /(NN-) P- N- /(NN-) I(P ,, P-)
-P log(P) - P- log(P- )
The difference is the information gain So, pick
the feature with the largest Info Gain I.e.
smallest residual info
Given k mutually exclusive and exhaustive events
E1.Ek whose probabilities are p1.pk The
information content (entropy) is defined as
S i -pi log2 pi A split is good if it
reduces the entropy..
23
The Information Gain Computation
P N /(NN-) P- N- /(NN-) I(P ,, P-)
-P log(P) - P- log(P- )
The difference is the information gain So, pick
the feature with the largest Info Gain I.e.
smallest residual info
Given k mutually exclusive and exhaustive events
E1.Ek whose probabilities are p1.pk The
information content (entropy) is defined as
S i -pi log2 pi A split is good if it
reduces the entropy..
24
I(1/2,1/2) -1/2 log 1/2 -1/2 log 1/2
1/2 1/2 1 I(1,0) 1log 1 0
log 0 0
A simple example
V(M) 2/4 I(1/2,1/2) 2/4 I(1/2,1/2)
1 V(A) 2/4 I(1,0) 2/4 I(0,1)
0 V(N) 2/4 I(1/2,1/2) 2/4
I(1/2,1/2) 1
So Anxious is the best attribute to split on Once
you split on Anxious, the problem is solved
25
(No Transcript)
26
m-fold cross-validation Split N examples into
m equal sized parts for i1..m train with
all parts except ith test with the ith part
Evaluating the Decision Trees
Lesson Every bias makes some concepts easier
to learn and others harder to learn
Learning curves Given N examples, partition
them into Ntr the training set and Ntest the test
instances Loop for i1 to Ntr Loop for
Ns in subsets of Ntr of size I Train the
learner over Ns Test the learned
pattern over Ntest and compute the accuracy
(correct)
27
Decision Stumps
This was used in the class but the next one is
the correct replacement
- Decision stumps are decision trees where the leaf
nodes do not necessarily have all ve or all ve
training examples - In general, with each leaf node, we can associate
a probability p that if we reach that leaf node,
the example is classified ve - When you reach that node, you toss a biased coin
(whose probability of heads is p and output ve
if the coin comes heads) - In normal decision trees, p is 0 or 1
- In decision stumps, 0 lt p lt 1
Splitting on feature fk
P N1 / N1N1-
Majority vote is better than tossing coin
Sometimes, the best decision tree for a problem
could be a decision stump (see coin toss example
next)
28
Problems with Info. Gain. Heuristics
- Feature correlation We are splitting on one
feature at a time - The Costanza party problem
- No obvious easy solution
- Overfitting We may look too hard for patterns
where there are none - E.g. Coin tosses classified by the day of the
week, the shirt I was wearing, the time of the
day etc. - Solution Dont consider splitting if the
information gain given by the best feature is
below a minimum threshold - Can use the c2 test for statistical significance
- Will also help when we have noisy samples
- We may prefer features with very high branching
- e.g. Branch on the universal time string for
Russell restaurant example - Branch on social security number to look
for patterns on who will get A - Solution gain ratio --ratio of information
gain with the attribute A to the information
content of answering the question What is the
value of A? - The denominator is smaller for attributes with
smaller domains.
29
Decision Stumps
- Decision stumps are decision trees where the leaf
nodes do not necessarily have all ve or all ve
training examples - Could happen either because examples are noisy
and mis-classified or because you want to stop
before reaching pure leafs - When you reach that node, you return the majority
label as the decision. - (We can associate a confidence with that decision
using the P and P-)
Splitting on feature fk
P N1 / N1N1-
Sometimes, the best decision tree for a problem
could be a decision stump (see coin toss example
next)
30
Bias Learning Accuracy
- Having weak bias (large hypothesis space)
- Allows us to capture more concepts
- ..increases learning cost
- May lead to over-fitting
31
Tastes Great/Less Filling
- Biases are essential for survival of an agent!
- You must need biases to just make learning
tractable - Whole object bias used by kids in language
acquisition - Biases put blinders on the learnerfiltering away
(possibly more accurate) hypotheses - God doesnt play dice with the universe
(Einstein) - Color of Skin relevant to predicting crime
(Billy BennettFormer Education Secretary)
32
Uses different biases in predicting Russels
waiting habbits
Decision Trees --Examples are used to --Learn
topology --Order of questions
If patronsfull and dayFriday then wait
(0.3/0.7) If waitgt60 and Reservationno then
wait (0.4/0.9)
Association rules --Examples are used to
--Learn support and confidence of
association rules
Neural Nets --Examples are used to --Learn
topology --Learn edge weights
Naïve bayes (bayesnet learning) --Examples are
used to --Learn topology --Learn CPTs
33
Mirror, Mirror, on the wall Which learning
bias is the best of all?
Well, there is no such thing, silly! --Each
bias makes it easier to learn some patterns and
harder (or impossible) to learn others -A
line-fitter can fit the best line to the data
very fast but wont know what to do if the data
doesnt fall on a line --A curve fitter can
fit lines as well as curves but takes longer
time to fit lines than a line fitter. --
Different types of bias classes (Decision trees,
NNs etc) provide different ways of naturally
carving up the space of all possible
hypotheses So a more reasonable question is --
What is the bias class that has a specialization
corresponding to the type of patterns that
underlie my data? ?Bias can be seen as a
sneaky way of letting background knowledge
in.. -- In this bias class, what is the most
restrictive bias that still can capture the true
pattern in the data?
--Decision trees can capture all boolean
functions --but are faster at capturing
conjunctive boolean functions --Neural nets can
capture all boolean or real-valued functions
--but are faster at capturing linearly separable
functions --Bayesian learning can capture all
probabilistic dependencies But are faster at
capturing single level dependencies (naïve bayes
classifier)
34
Fitting test cases vs. predicting future
cases The BIG TENSION.
Review
2
1
3
Why not the 3rd?
35
12/3 The Last Class??
- ?Fill Return the participation forms
- ?Todays Agenda Perceptrons (until 1130)
- ?Interactive Review
- ?Take Home Final will be delivered by e-mail Wed
- Will be due 12/10
36
Uses different biases in predicting Russels
waiting habbits
Decision Trees --Examples are used to --Learn
topology --Order of questions
K-nearest neighbors
If patronsfull and dayFriday then wait
(0.3/0.7) If waitgt60 and Reservationno then
wait (0.4/0.9)
Association rules --Examples are used to
--Learn support and confidence of
association rules
SVMs
Neural Nets --Examples are used to --Learn
topology --Learn edge weights
Naïve bayes (bayesnet learning) --Examples are
used to --Learn topology --Learn CPTs
37
Decision Surface Learning(aka Neural Network
Learning)
- Idea Since classification is really a question
of finding a surface to separate the ve examples
from the -ve examples, why not directly search in
the space of possible surfaces? - Mathematically, a surface is a function
- Need a way of learning functions
- Threshold units
38
Neural Net is a collection of with
interconnections
threshold units
differentiable
39
The Brain Connection
A Threshold Unit
Threshold Functions
differentiable
is sort of like a neuron
40
Perceptron Networks
What happened to the Threshold? --Can model
as an extra weight with static input
41
Perceptron Learning
- Perceptron learning algorithm
- Loop through training examples
- If the activation level of the output unit is 1
when it should be 0, reduce the weight on the
link to the jth input unit by aIj, where Ii is
the ith input value and a a learning rate - If the activation level of the output unit is 0
when it should be 1, increase the weight on the
link to the ith input unit by aIj - Otherwise, do nothing
- Until convergence
Iterative search! --node -gt network weights
--goodness -gt error Actually a gradient
descent search
A nice applet at
http//neuron.eng.wayne.edu/java/Perceptron/New38.
html
42
Perceptron Learning as Gradient Descent Search in
the weight-space
Often a constant learning rate parameter is
used instead
Ij
I
43
Perceptron Training in Action
A nice applet at
http//neuron.eng.wayne.edu/java/Perceptron/New38.
html
44
Can Perceptrons Learn All Boolean Functions?
--Are all boolean functions linearly separable?
45
Comparing Perceptrons and Decision Trees in
Majority Function and Russell Domain
Decision Trees
Perceptron
Decision Trees
Perceptron
Majority function
Russell Domain
Majority function is linearly seperable..
Russell domain is apparently not....
Encoding one input unit per attribute. The unit
takes as many distinct real values as the size
of attribute domain
46
Max-Margin Classification Support Vector
Machines
- Any line that separates the ve ve examples
is a solution - And perceptron learning finds one of them
- But could we have a preference among these?
- may want to get the line that provides maximum
margin (equidistant from the nearest ve/-ve) - The nereast ve and ve holding up the line are
called support vectors - This changes the problem into an optimization
one - Quadratic Programming can be used to directly
find such a line
Learning is Optimization after all!
47
Lagrangian Dual
48
Two ways to learn non-linear decision surfaces
- First transform the data into higher dimensional
space - Find a linear surface
- Which is guaranteed to exist
- Transform it back to the original space
- TRICK is to do this without explicitly doing a
transformation
- Learn non-linear surfaces directly (as
multi-layer neural nets) - Trick is to do training efficiently
- Back Propagation to the rescue..
49
Linear Separability in High Dimensions
Kernels allow us to consider separating
surfaces in high-D without first converting
all points to high-D
50
Kernelized Support Vector Machines
- Turns out that it is not always necessary to
first map the data into high-D, and then do
linear separation - The quadratic programming formulation for SVM
winds up using only the pair-wise dot product of
training vectors - Dot product is a form of similarity metric
between points - If you replace that dot product by any non-linear
function, you will, in essence, be transforming
data into some high-dimensional space and then
finding the max-margin linear classifier in that
space - Which will correspond to some wiggly surface in
the original dimension - The trick is to find the RIGHT similarity
function - Which is a form of prior knowledge
51
Kernelized Support Vector Machines
- Turns out that it is not always necessary to
first map the data into high-D, and then do
linear separation - The quadratic programming formulation for SVM
winds up using only the pair-wise dot product of
training vectors - Dot product is a form of similarity metric
between points - If you replace that dot product by any non-linear
function, you will, in essence, be tranforming
data into some high-dimensional space and then
finding the max-margin linear classifier in that
space - Which will correspond to some wiggly surface in
the original dimension - The trick is to find the RIGHT similarity
function - Which is a form of prior knowledge
52
Domain-knowledge Learning
Those who ignore easily available domain
knowledge are doomed to re-learn it
Santayanas brother
- Classification learning is a problem addressed by
both people from AI (machine learning) and
Statistics - Statistics folks tend to distrust
domain-specific bias. - Let the data speak for itself
- ..but this is often futile. The very act of
describing the data points introduces bias (in
terms of the features you decided to use to
describe them..) - but much human learning occurs because of strong
domain-specific bias.. - Machine learning is torn by these competing
influences.. - In most current state of the art algorithms,
domain knowledge is allowed to influence
learning only through relatively narrow
avenues/formats (E.g. through kernels) - Okay in domains where there is very little (if
any) prior knowledge (e.g. what part of proteins
are doing what cellular function) - ..restrictive in domains where there already
exists human expertise..
53
Multi-layer Neural Nets
How come back-prop doesnt get stuck in local
minima? One answer It is actually hard for
local minimas to form in high-D, as the
trough has to be closed in all dimensions
54
(No Transcript)
55
Multi-Network Learning can learn Russell Domains
Decision Trees
Decision Trees
Multi-layer networks
Perceptron
Russell Domain
but does it slowly
56
Practical Issues in Multi-layer network learning
- For multi-layer networks, we need to learn both
the weights and the network topology - Topology is fixed for perceptrons
- If we go with too many layers and connections, we
can get over-fitting as well as sloooow
convergence - Optimal brain damage
- Start with more than needed hidden layers as well
as connections after a network is learned,
remove the nodes and connections that have very
low weights retrain
57
Humans make 0.2 Neumans (postmen) make 2
Other impressive applications --no-hands
across america --learning to speak
K-nearest-neighbor The test examples class is
determined by the class of the majority of
its k nearest neighbors Need to define an
appropriate distance measure --sort of easy
for real valued vectors --harder for
categorical attributes
58
Decision Trees vs. Neural Nets
- Can handle real-valued attributes
- Can learn any non-linear decision surface
- Incremental as new examples arrive, the network
can adapt. - Good at handling noise
- Convergence is quite slow
- Faster at learning linear ones
- Learned concept is represented by the weights and
topology of the network (so hard to understand) - Consider understanding Einstein by dissecting his
brain. - Double edged argumentthere are many learning
tasks for whion ch we do not know how to
articulated what we have learned. Eg. Face
recognition word recognition
- Work well for discrete attributes.
- Converge fast for conjunctive concepts
- Non-incremental (looks at all the examples at
once) - Not very good at handling noise
- Generally good at avoiding irrelevant attributes
- Easy to understand the learned concept
Why is it important to understand what is
learned? --The military hidden tank photos
example
59
(No Transcript)
60
(No Transcript)
61
(No Transcript)
62
True hypothesis eventually dominates
probability of indefinitely producing
uncharacteristic data ?0
63
Bayesian prediction is optimal (Given the
hypothesis prior, all other predictions are
less likely)
64
Also, remember the Economist article that shows
that humans have strong priors..
65
..note that the Economist article says humans
are able to learn from few examples only because
of priors..
66
So, BN learning is just probability estimation!
(as long as data is complete!)
67
How Well (and WHY) DOES NBC WORK?
- Naïve bayes classifier is darned easy to
implement - Good learning speed, classification speed
- Modest space storage
- Supports incrementality
- It seems to work very well in many scenarios
- Lots of recommender systems (e.g. Amazon books
recommender) use it - Peter Norvig, the director of Machine Learning at
GOOGLE said, when asked about what sort of
technology they use Naïve bayes - But WHY?
- NBCs estimate of class probability is quite bad
- BUT classification accuracy is different from
probability estimate accuracy - Domingoes/Pazzani 1996 analyze this
68
(No Transcript)
69
(No Transcript)
70
(No Transcript)
71
(No Transcript)
72
Bayes Network Learning
- Bias The relation between the class label and
class attributes is specified by a Bayes Network. - Approach
- Guess Topology
- Estimate CPTs
- Simplest case Naïve Bayes
- Topology of the network is class label causes
all the attribute values independently - So, all we need to do is estimate CPTs
P(attribClass) - In Russell domain, P(Patronswillwait)
- P(Patronsfullwillwaityes)
- training examples where patronsfull and
will waityes - training examples where will waityes
- Given a new case, we use bayes rule to compute
the class label
Class label is the disease attributes are
symptoms
73
Naïve Bayesian Classification
- Problem Classify a given example E into one of
the classes among C1, C2 ,, Cn - E has k attributes A1, A2 ,, Ak and each Ai can
take d different values - Bayes Classification Assign E to class Ci that
maximizes P(Ci E) - P(Ci E) P(E Ci) P(Ci) / P(E)
- P(Ci) and P(E) are a priori knowledge (or can be
easily extracted from the set of data) - Estimating P(ECi) is harder
- Requires P(A1v1 A2v2.AkvkCi)
- Assuming d values per attribute, we will need ndk
probabilities - Naïve Bayes Assumption Assume all attributes are
independent P(E Ci) P P(Aivj Ci ) - The assumption is BOGUS, but it seems to WORK
(and needs only ndk probabilities
74
NBC in terms of BAYES networks..
NBC assumption
More realistic assumption
75
Estimating the probabilities for NBC
- Given an example E described as A1v1
A2v2.Akvk we want to compute the class of E - Calculate P(Ci A1v1 A2v2.Akvk) for all
classes Ci and say that the class of E is the
one for which P(.) is maximum - P(Ci A1v1 A2v2.Akvk)
- P P(vj Ci ) P(Ci) / P(A1v1
A2v2.Akvk) - Given a set of training N examples that have
already been classified into n classes Ci - Let (Ci) be the number of
examples that are labeled as Ci - Let (Ci, Aivi) be the number of
examples labeled as Ci - that have attribute Ai
set to value vj - P(Ci) (Ci)/N
- P(Aivj Ci) (Ci, Aivi) /
(Ci)
76
Example
P(willwaityes) 6/12 .5 P(Patronsfullwillw
aityes) 2/60.333 P(Patronssomewillwaityes
) 4/60.666
Similarly we can show that P(Patronsfullwillw
aitno) 0.6666
P(willwaityesPatronsfull) P(patronsfullwill
waityes) P(willwaityes)
--------------------------------------------------
---------
P(Patronsfull)
k
.333.5 P(willwaitnoPatronsfull) k 0.666.5
77
Using M-estimates to improve probablity estimates
- The simple frequency based estimation of
P(AivjCk) can be inaccurate, especially when
the true value is close to zero, and the number
of training examples is small (so the probability
that your examples dont contain rare cases is
quite high) - Solution Use M-estimate
- P(Aivj Ci) (Ci, Aivi)
mp / (Ci) m - p is the prior probability of Ai taking the value
vi - If we dont have any background information,
assume uniform probability (that is 1/d if Ai can
take d values) - m is a constantcalled equivalent sample size
- If we believe that our sample set is large
enough, we can keep m small. Otherwise, keep it
large. - Essentially we are augmenting the (Ci) normal
samples with m more virtual samples drawn
according to the prior probability on how Ai
takes values - Popular values p1/V and mV where V is the
size of the vocabulary
Also, to avoid overflow errors do addition of
logarithms of probabilities (instead of
multiplication of probabilities)
78
How Well (and WHY) DOES NBC WORK?
- Naïve bayes classifier is darned easy to
implement - Good learning speed, classification speed
- Modest space storage
- Supports incrementality
- It seems to work very well in many scenarios
- Lots of recommender systems (e.g. Amazon books
recommender) use it - Peter Norvig, the director of Machine Learning at
GOOGLE said, when asked about what sort of
technology they use Naïve bayes - But WHY?
- NBCs estimate of class probability is quite bad
- BUT classification accuracy is different from
probability estimate accuracy - Domingoes/Pazzani 1996 analyze this
79
Sahami et als Solution for SPAM detection
- use standard Term Vector Space model developed
by Information Retrieval field (similar to
AdEater) - 1 e-mail message ? single fixed-width feature
vector - have 1 bit in this vector for each term that
occurs in some message in E (plus a bunch of
domain-specific featureseg, when message was
sent) - learning algorithm
- use standard Naive Bayes algorithm
80
Feature Selection
- A problem -- too many features -- each vector x
contains several thousand features. - Most come from word features -- include a word
if any e-mail contains it (eg, every x contains
an opossum feature even though this word occurs
in only one message). - Slows down learning and predictoins
- May cause lower performance
- The Naïve Bayes Classifier makes a huge
assumption -- the independence assumption. - A good strategy is to have few features, to
minimize the chance that the assumption is
violated. - Ideally, discard all features that violate the
assumption. (But if we knew these features, we
wouldnt need to make the naive independence
assumption!) - Feature selection a few thousand ? 500
features
81
Feature-Selection approach
- Lots of ways to perform feature selection
- FEATURE SELECTION DIMENSIONALITY REDUCTION
- One simple strategy mutual information
- Suppose we have two random variables A and B.
- Mutual information MI(A,B) is a numeric measure
of what we can conclude about A if we know B, and
vice-versa. - MI(A,B) Pr(AB) log(Pr(AB)/(Pr(A)Pr(B)))
- Example If A and B are independent, then we
cant conclude anything MI(A, B) 0 - Note that MI can be calculated without needing
conditional probabilities.
82
Mutual Information, continued
- Check our intuition independence -gt MI(A,B)0
MI(A,B) Pr(AB) log(Pr(AB)/(Pr(A)Pr(B)))
Pr(AB) log(Pr(A)Pr(B)/(Pr(A)Pr(B
))) Pr(AB) log 1
0 - Fully correlated, it becomes the information
content - MI(A,A) - Pr(A)log(Pr(A))
- it depends on how uncertain the event is
notice that the expression becomes maximum (1)
when Pr(A).5 this makes sense since the most
uncertain event is one whose probability is .5
(if it is .3 then we know it is likely not to
happen if it is .7 we know it is likely to
happen).
83
MI and Feature Selection
- Back to feature selection Pick features Xi that
have high mutual information with the junk/legit
classification C. - These are exactly the features that are good for
prediction - Pick 500 features Xi with highest value MI(Xi, C)
- NOTE NBCs estimate of probabilities is
actually quite a bit wrong but they still got by
with those.. - Also, note that this analysis looks at each
feature in isolation and may thus miss highly
predictive word groups whose individual words are
quite non-predictive - e.g. free and money may have low MI, but
Free money may have higher MI. - A way to handle this is to look at MI of not just
words but subsets of words - (in the worst case, you will need to compute 2n
MIs ?) - So instead, Sahami et. Al. add domain specific
phrases separately.. - Note Theres no reason that the highest-MI
features are the ones that least violate the
independence assumption -- this is just a
heuristic!
84
MI based feature selection vs. LSI
- Both MI and LSI are dimensionality reduction
techniques - MI is looking to reduce dimensions by looking at
a subset of the original dimensions - LSI looks instead at a linear combination of the
subset of the original dimensions (Good Can
automatically capture sets of dimensions that are
more predictive. Bad the new features may not
have any significance to the user) - MI does feature selection w.r.t. a classification
task (MI is being computed between a feature and
a class) - LSI does dimensionality reduction independent of
the classes (just looks at data variance)
85
Reinforcement Learning
- Based on slides from Bill Smart
- http//www.cse.wustl.edu/wds/
86
What is RL?
- a way of programming agents by reward and
punishment without needing to specify how the
task is to be achieved - Kaelbling, Littman, Moore, 96
87
Basic RL Model
- Observe state, st
- Decide on an action, at
- Perform action
- Observe new state, st1
- Observe reward, rt1
- Learn from experience
- Repeat
- Goal Find a control policy that will maximize
the observed rewards over the lifetime of the
agent
A
S
R
88
An Example Gridworld
- Canonical RL domain
- States are grid cells
- 4 actions N, S, E, W
- Reward for entering top right cell
- -0.01 for every other move
- Minimizing sum of rewards ? Shortest path
- In this instance
1
89
The Promise of Learning
90
The Promise of RL
- Specify what to do, but not how to do it
- Through the reward function
- Learning fills in the details
- Better final solutions
- Based of actual experiences, not programmer
assumptions - Less (human) time needed for a good solution
91
Learning Value Functions
- We still want to learn a value function
- Were forced to approximate it iteratively
- Based on direct experience of the world
- Four main algorithms
- Certainty equivalence
- Temporal Difference (TD) learning
- Q-learning
- SARSA
92
Certainty Equivalence
- Collect experience by moving through the world
- s0, a0, r1, s1, a1, r2, s2, a2, r3, s3, a3, r4,
s4, a4, r5, s5, ... - Use these to estimate the underlying MDP
- Transition function, T S?A ? S
- Reward function, R S?A?S ? ?
- Compute the optimal value function for this MDP
- And then compute the optimal policy from it
93
Temporal Difference (TD)
Sutton, 88
- TD-learning estimates the value function directly
- Dont try to learn the underlying MDP
- Keep an estimate of Vp(s) in a table
- Update these estimates as we gather more
experience - Estimates depend on exploration policy, p
- TD is an on-policy method
94
TD-Learning Algorithm
- Initialize Vp(s) to 0, ?s
- Observe state, s
- Perform action, p(s)
- Observe new state, s, and reward, r
- Vp(s) ? (1-a)Vp(s) a(r gVp(s))
- Go to 2
- 0 a 1 is the learning rate
- How much attention do we pay to new experiences
95
TD-Learning
- Vp(s) is guaranteed to converge to V(s)
- After an infinite number of experiences
- If we decay the learning rate
- will work
- In practice, we often dont need value
convergence - Policy convergence generally happens sooner
96
Actor-Critic Methods
Barto, Sutton, Anderson, 83
- TD only evaluates a particular policy
- Does not learn a better policy
- We can change the policy as we learn V
- Policy is the actor
- Value-function estimate is the critic
- Success is generally dependent on the starting
policy being good enough
Policy (actor)
a
V
Value Function (critic)
r
s
World
97
Q-Learning
Watkins Dayan, 92
- Q-learning iteratively approximates the
state-action value function, Q - Again, were not going to estimate the MDP
directly - Learns the value function and policy
simultaneously - Keep an estimate of Q(s, a) in a table
- Update these estimates as we gather more
experience - Estimates do not depend on exploration policy
- Q-learning is an off-policy method
98
Q-Learning Algorithm
- Initialize Q(s, a) to small random values, ?s, a
- Observe state, s
- Pick an action, a, and do it
- Observe next state, s, and reward, r
- Q(s, a) ? (1 - a)Q(s, a) a(r gmaxaQ(s, a))
- Go to 2
- 0 a 1 is the learning rate
- We need to decay this, just like TD
99
Picking Actions
- We want to pick good actions most of the time,
but also do some exploration - Exploring means that we can learn better policies
- But, we want to balance known good actions with
exploratory ones - This is called the exploration/exploitation
problem
100
Picking Actions
- e-greedy
- Pick best (greedy) action with probability e
- Otherwise, pick a random action
- Boltzmann (Soft-Max)
- Pick an action based on its Q-value
- , where t is
the temperature
101
SARSA
- SARSA iteratively approximates the state-action
value function, Q - Like Q-learning, SARSA learns the policy and the
value function simultaneously - Keep an estimate of Q(s, a) in a table
- Update these estimates based on experiences
- Estimates depend on the exploration policy
- SARSA is an on-policy method
- Policy is derived from current value estimates
102
SARSA Algorithm
- Initialize Q(s, a) to small random values, ?s, a
- Observe state, s
- Pick an action, a, and do it (just like
Q-learning) - Observe next state, s, and reward, r
- Q(s, a) ? (1-a)Q(s, a) a(r gQ(s, p(s)))
- Go to 2
- 0 a 1 is the learning rate
- We need to decay this, just like TD
103
On-Policy vs. Off Policy
- On-policy algorithms
- Final policy is influenced by the exploration
policy - Generally, the exploration policy needs to be
close to the final policy - Can get stuck in local maxima
- Off-policy algorithms
- Final policy is independent of exploration policy
- Can use arbitrary exploration policies
- Will not get stuck in local maxima
Given enough experience
104
Convergence Guarantees
- The convergence guarantees for RL are in the
limit - The word infinite crops up several times
- Dont let this put you off
- Value convergence is different than policy
convergence - Were more interested in policy convergence
- If one action is really better than the others,
policy convergence will happen relatively quickly
105
Rewards
- Rewards measure how well the policy is doing
- Often correspond to events in the world
- Current load on a machine
- Reaching the coffee machine
- Program crashing
- Everything else gets a 0 reward
- Things work better if the rewards are incremental
- For example, distance to goal at each step
- These reward functions are often hard to design
These are sparse rewards
These are dense rewards
106
The Markov Property
- RL needs a set of states that are Markov
- Everything you need to know to make a decision is
included in the state - Not allowed to consult the past
- Rule-of-thumb
- If you can calculate the reward
function from the state without
any additional information,
youre OK
K
S
G
107
But, Whats the Catch?
- RL will solve all of your problems, but
- We need lots of experience to train from
- Taking random actions can be dangerous
- It can take a long time to learn
- Not all problems fit into the MDP framework
108
Learning Policies Directly
- An alternative approach to RL is to reward whole
policies, rather than individual actions - Run whole policy, then receive a single reward
- Reward measures success of the whole policy
- If there are a small number of policies, we can
exhaustively try them all - However, this is not possible in most interesting
problems
109
Policy Gradient Methods
- Assume that our policy, p, has a set of n
real-valued parameters, q q1, q2, q3, ... , qn
- Running the policy with a particular q results in
a reward, rq - Estimate the reward gradient, , for each
qi
110
Policy Gradient Methods
- This results in hill-climbing in policy space
- So, its subject to all the problems of
hill-climbing - But, we can also use tricks from search, like
random restarts and momentum terms - This is a good approach if you have a
parameterized policy - Typically faster than value-based methods
- Safe exploration, if you have a good policy
- Learns locally-best parameters for that policy
111
An Example Learning to Walk
Kohl Stone, 04
- RoboCup legged league
- Walking quickly is a big advantage
- Robots have a parameterized gait controller
- 11 parameters
- Controls step length, height, etc.
- Robots walk across soccer pitch and are timed
- Reward is a function of the time taken
112
An Example Learning to Walk
- Basic idea
- Pick an initial q q1, q2, ... , q11
- Generate N testing parameter settings by
perturbing q - qj q1 d1, q2 d2, ... , q11 d11, di ?
-e, 0, e - Test each setting, and observe rewards
- qj ? rj
- For each qi ? q
- Calculate q1, q10, q1- and set
- Set q ? q, and go to 2
Average reward when qni qi - di
113
An Example Learning to Walk
Initial
Final
Video Nate Kohl Peter Stone, UT Austin
114
Value Function or Policy Gradient?
- When should I use policy gradient?
- When theres a parameterized policy
- When theres a high-dimensional state space
- When we expect the gradient to be smooth
- When should I use a value-based method?
- When there is no parameterized policy
- When we have no idea how to solve the problem
115
Summary for Part I
- Background
- MDPs, and how to solve them
- Solving MDPs with dynamic programming
- How RL is different from DP
- Algorithms
- Certainty equivalence
- TD
- Q-learning
- SARSA
- Policy gradient