Simple Target Identification using Unconstrained

1
Simple Target Identification using Unconstrained
E-Pulse Technique
Student Lui Hoi Shun Antony Supervisor
A/Prof Nicholas Shuley
Objective Investigate the performance of the
Resonance Based Radar Target Identification
Algorithm, E-Pulse Technique, for identifying
and differentiating different aircraft models.

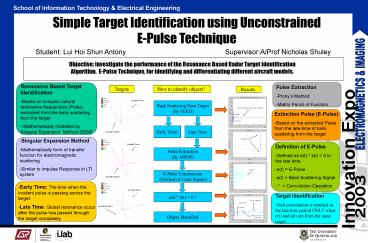
• Resonance Based Target Identification
• Based on complex natural resonance frequencies
  (Poles) extracted from the back scattering from
  the target
• Mathematically modelled by Singular Expansion
  Method (SEM)

• Poles Extraction
• Pronys Method
• Matrix Pencil of Function

How to identify objects?
Targets
Results
Incident Wave
Back Scattering from Target (by FEKO)
Back Scattering Signal from the Target

• Extinction Pulse (E-Pulse)
• Based on the extracted Poles from the late-time
  of back scattering from the target

Late Time
Early Time
Late Time
Aircraft Model 1
Extracted Poles

• Singular Expansion Method
• Mathematically form of transfer function for
  electromagnetic scattering
• Similar to Impulse Response in LTI system

Incident Wave

• Definition of E-Pulse
• Defined as e(t) s(t) 0 in the late time
• e(t) E-Pulse
• s(t) Back Scattering Signal
• Convolution Operation

Poles Extraction (By MPOF)
E-Pulse
E-Pulse Construction (Method of Least Square)
Aircraft Model 2

• Early Time The time when the incident pulse is
  passing across the target.
• Late Time Global resonance occur after the pulse
  has passed through the target completely.

Incident Wave
e(t) s(t) 0 ?

• Target Identification
• Null convolution is resulted in the late time
  period ONLY when e(t) and s(t) are from the same
  target.

Back Scattering
Late Time
Aircraft Model 3
Object Identified
Null Convolution at late time