Data Compressing Codes (Communications Block Diagram)

1
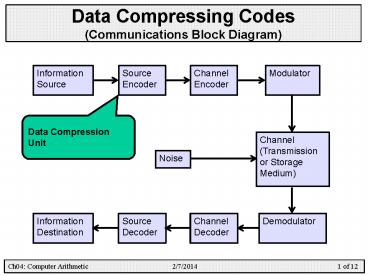
Data Compressing Codes(Communications Block
Diagram)
Information Source
Channel Encoder
Modulator
Source Encoder
Data Compression Unit
Channel (Transmission or Storage Medium)
Noise
Information Destination
Source Decoder
Channel Decoder
Demodulator
2
Data-Compressing CodesDefinitions

• Data compression (or source coding )
• is the process of encoding information using
  fewer symbols than an unencoded representation
  would use through use of specific encoding
  schemes .
• Lossless compression
• Attempts to remove statistically redundant
  information from the source data. The source data
  is recovered perfectly from the encoding.
• Lossy compression
• Attempts to remove perceptually irrelevant
  information from the source data. Removing the
  irrelevant information tends to increase the
  redundant information, making data compression
  possible. The source data is recovered
  imperfectly from the encoding.

3
Data-Compressing CodesDefinitions

• Compression Ratio
• Uncompressed sizecompressed size
• Example uncompressed size 1024 bits,
  compressed size 256 bits. Therefore, the CR is
  41

4
What is Statistical Redundancy?

• Most real-world data has statistical redundancy.
• Statistical redundancy is generally non-trivially
  embedded in data.
• Statistical redundancy appears as patterns hidden
  in the data.
• Data compression is achieved by encoding the
  patterns instead of the actual data.
• The encoding of patterns requires less symbols.
• The problem of data compression is to find the
  hidden patterns, extract them, and then encode
  them efficiently.

5
Statistical Redundancy Locator Run-Length
Encoding (RLE)

• Runs of data are stored as a single data value
  and count, rather than as the original run.
• For example, consider a screen containing plain
  black text on a solid white background.
• Let us take a hypothetical single scan line, with
  B representing a black pixel and W representing
  white
• WWWWWWWWWWWWBWWWWWWWWWWWWBBBW . . .
• RLE yields the code
• 12WB12W3B24WB14W
• Twelve W's, one B, twelve W's, three B's, etc.
• CR is 6716.

6
Statistical Redundancy Locator Symbol
Probabilities

• For example, in English text,
• The letter e is much more common than the
  letter z.
• The probability that the letter q will be
  followed by the letter z is very small.
• It would be inefficient to encode each symbol
  with the same size of codeword.

7
Statistical Redundancy Locator Huffman Code

• Construct a code that assigns frequently used
  source-symbols short codes, and infrequently used
  source-symbols longer codes.
• Variable length codeword.
• Average codeword length

8
Huffman Code Average Length of Codeword

• Fixed Length Codeword System
• Let SL Symbol Length.
• (1/n)SUM(i1n) SLi SL, where SLi symbol
  length of codeword i.
• Variable Length Codeword System
• Note (1/n)SUM(i1n) SLi SUM(i1n)(1/n)SLi
  , where (1/n) represents the equal probability
  of a symbol appearing in a message.
• SUM(i1n)(Pi )SLi , where Pi is the
  probability of symbol i appearing in a message.
• Average Length SUM(i1n)Pi SLi

9
Huffman CodeExample Alphabet A,B,C,D,E,F
Symbol Code
A 0
B 10
C 110
D 1110
E 1111
1x0.5000 2x0.2500 3x0.1250 4x0.0625 4x0.0625 1.875
Average Codeword Length 1.875 bits per symbol
10
Huffman CodeExample Alphabet A,B,C,D,E
0
Symbol Code
A 00
B 01
C 10
D 11
A 0.25
0
0.5
B 0.25
1
1.0
0
C 0.25
1
0.5
D 0.25
1
Average Codeword Length 2 bits per symbol
11
Statistical Redundancy Locator Quad trees
12
Statistical Redundancy Locator Quad trees
CR is 6429
13
What is Perceptual Irrelevancy?

• Information that is not relevant to the observer.
• Examples,
• Image, moving pictures, audio, speech.
• Removing irrelevant information increase the
  amount of redundant information.
• Consider an image 1024x1024 pixels that have
  values within the range from 0000 0000 to 0001
  1001. The average human visual system cannot
  distinguish these pixels.
• RLE can represent the entire image using 3 bytes
  (00, 0400)