Real Fluids

1
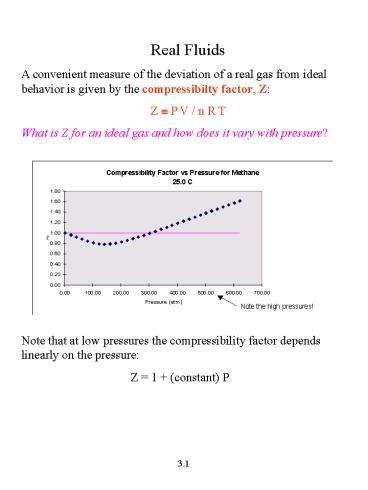
Real Fluids A convenient measure of the deviation
of a real gas from ideal behavior is given by the
compressibilty factor, Z Z ? P V / n R T What
is Z for an ideal gas and how does it vary with
pressure?
Note that at low pressures the compressibility
factor depends linearly on the pressure Z 1
(constant) P
2
The ideal gas equation of state can be improved
by removing the restriction that the gas
molecules or atoms have zero volume. Note that in
the limit as temperature goes to zero on the
Kelvn scale the molar volume of an ideal gas also
goes to zero lim V R T / P ---gt 0
T--gt0 Why is this an absurd result for a real
gas? We can improve this result by adding a
constant term to the molar volume lim V R T /
P b ---gt ? T--gt0 The term b is roughly a
measure of what molecular property? At this
point our improved equation of state, which
accounts for the finite size of real molecules,
has the form P n R T / ( V n b ) R T /
( Vm b ) Note that for this improved equation
of state Z depends linearly on P Z 1 ( b /
R T ) P
3
This improved equation of state can be further
improved by removing the 2nd ideal gas
restriction and accounting for the attractive
forces that the molecules and atoms exert on each
other. Since the attractive interactions between
the molecules or atoms in the bulk fluid would
decrease the momentum transferred in collisions
with the container walls, these interactions
decrease the pressure exerted by the
gas. Since the molecules or atoms are
mutually attracting each other, the reduction in
pressure is proportional to the square of the
concentration of the molecules or atoms
4
Incorporating both of these improvements on the
ideal gas law yields the van der Waals equation
of state P n R T / (V- n b) - a C2
n R T / (V - n b) - a n2
/ V2 The proportionality constant a is a measure
of the strength of the intermolecular or
interatomic attractions. How should the
proportionality contstant a vary with the number
of electrons in the molecule or atom? The van der
Waals equation of state is an example of a two
parameter equation of state, where the parameters
a and b are determined empirically by fitting
experimental pressure, volume, temperature (PVT)
data to the equation. What does the van der Waals
equation reduce to in the limit of low pressure
and high temperature? The equation, while
modeling gas behavior more precisely than the
ideal gas equation, is less general than the
ideal gas equation in that a and b are different
for different gases. Another drawback of the van
der Waals equation, when compared to the ideal
gas equation is that the equation is cubic in the
volume, the number of moles, and their ratio, the
molar volume.
5
Johannes Diderik van der Waals
Johannes Diderik van der Waals was born
November 23th, 1837 in Leiden as the eldest
son in a family with eight children. Initially
J.D. studied to be an elementary school
teacher and taught school between 1856 and
1861. While studying to be a Head Master he
attended lectures on Mathematics, Physics and
Astronomy at Leiden University and starting in
1866 was engaged by a secondary school in The
Hague as teacher in Physics and Mathematics.
After seven years he became their subsitute
director and in 1877 director. In 1873 he
graduated from Leiden University. In his thesis
Over de continuïteit van de gas- en
vloeistoftoestand (On the continuity of the
gaseous and liquid states) he published the
well-known law, which is named after him. P
n R T / (V - n b) - a n2 / V2 This law is a
correction on the law of ideal gases. It
considers the own volume of the gas molecules and
assumes a force between these molecules. Today
these forces are known as "Van-der-Waals-forces".
With this law, the existence of condensation and
the critical temperature of gases could be
predicted.
6
In 1877 J.D. becomes the first professor of
Physics at the University "Illustre" in
Amsterdam. Van der Waals was an excellent
theoretical physicist and in Leiden he provided
theoretical help to Kamerlingh Onnes in his
successful attempt to liquify gasses. Van der
Waals made a number of important contributions to
the science of physics. In 1880 he formulated
his "law of the corresponding states", in 1893 he
developed a theory for capillary phenomena, and
in 1891 a theory for the behaviour of mixtures of
two materials. From 1875 to 1895 he was a
member of the "Koninklijke Academie van
Wetenschappen" ( Dutch Royal Academy of Science).
In November of 1895 he and Kamerlingh Onnes
became the first physicists to be honoured with
the golden medal of the Genootschap ter
bevordering van natuur-, genees- en heelkunde
(Society for the benefit of physics, medical
science and surgery) at Amsterdam. He is one of
only twelve foreign members of the Academie des
Sciences in Paris. In 1910 he received the Nobel
prize in Physics joining Kamerlingh Onnes,
Zeeman, Lorentz and Van 't Hoff as the fifth
Dutch physisist to receive this honour. J.D. van
der Waals died march 8th, 1923 at the age of 85.
This material is taken from the WEB site
http//www.vdwaals.nl/ (of course you have to
read Dutch to understand it) maintained by a
student society named after J. D. van der Waals
at Technische Universisteit Eindhoven.
7
Summarizing the van der Waals equation of state
is P R T / (Vm - b) - a / Vm2 Where Vm is
the molar volume, V/n. Some other well known two
parameter equations of state are the
Peng-Robinson EQS P R T / (Vm - b) - a /
Vm (Vm b) b (Vm b) Peng and Robinson are
Chemical Engineers whose work on the phase
behavior of fluids of interest to the Petroleum
Industry has led to the formation of the DB
Robinson Group of Companies that provides quality
phase behavior and fluid property technology to
the petroleum and petrochemical industries
http//www.dbra.com/ which appears to have been
purchased by Schlumberger. the Redlich-Kwong
EQS P R T / (Vm - b) - a / (Vm(Vm b)
T1/2) and the Berthelot EQS P R T / (Vm -
b) - a / (Vm2 T) What do these equations have in
common? Are the constants a and b in the above
equations all the same?
8
While real gas equations of state can model
liquids as well as gases, PVT data for condensed
phases is often expressed in terms of isobaric
coefficients of thermal expansion or in terms of
isothermal compressibilities. The cubical
isobaric coefficient of thermal expansion, a,
measures the fractional change in volume of some
substance as the temperature on the substance is
changed isobarically a ? (1/V) (?V/?T)p This
equation can be viewed as an equation of state
for a condensed phase at constant pressure. The
cubical isobaric coefficient of thermal expansion
for liquid water is a 2.5721x10-4 K-1 The
partial differential equation defining a is
easily solved by separating variables and
integrating Vo ?V dV/V To ? T a dT The lower
limits on these integrals represent a temperature
To at which the volume Vo of the substance could
be determined. Could you determine V o, if you
knew the density, r o, at T o ? The upper
limits have been left unspecified to give after
integration a function describing how the volume
varies with temperature ln (V/ Vo) a (T -
To) Solving for V we get V Vo e a (T -
To) Vo e - a To e a T
9
An approximate, but often encountered, form of
this relation can be obtained by expanding the
exponential as a power series and ignoring, since
a is generally quite small, terms that are
quadratic and higher in the temperature V _at_
Vo 1 a (T - To) Vo 1 a DT Can you
derive an equation relating the density of a
condensed phase to temperature? Using the
following density versus temperature data for
liquid Hg - 10.0 oC 13.6202 g/mL 15.0 oC
13.5585 g/mL - 5.0 oC 13.6078
g/mL 20.0 oC 13.5462 g/mL -
0.0 oC 13.5955 g/mL 25.0 oC 13.5340 g/mL
5.0 oC 13.5832 g/mL 30.0 oC
13.5217 g/mL 10.0 oC 13.5708
g/mL 35.0 oC 13.5095 g/mL determine a value
for the cubical coefficient of thermal expansion
of liquid Hg in units of K-1. The linear
coefficient of thermal expansion of fused quartz
glass is a L 5.5x10-7 K-1 (1/L)
(?L/?T)p What is the cubical coefficient of
thermal expansion of this glass?
10
A barometer calibrated at 15.0 oC correctly reads
the atmospheric pressure of 620.0 mm Hg when it
is used at 15.0 oC. What will this barometer
read when the atmospheric pressure is 620 mm Hg
and the temperature is 30.0 oC? The linear
isobaric coefficient of thermal expansion of Hg
is 5.46x10-4 K-1. Ignore the thermal expansion
of the glass. A thermocline marks a region of
rapidly changing temperature. In the oceans the
thermocline occurs at 1000 meters below the
oceans surface and denotes the depth where warm
rapidly mixing surface waters transition to
deeper denser more slowly mixing ocean waters at
4 oC. By how many centimeters would the
elevation of the ocean surface increase, if
global warming resulted in an 1 oC increase in
the average temperature of the oceans surface
water. Take the average radius of the earth to be
6371.315 km. The cubical isobaric
coefficient of thermal expansion for liquid water
is a 2.5721x10-4 K-1.
11
The isothermal compressibility, b, measures the
fractional change in volume of some substance as
the pressure on the substance is changed
isothermally b ? - (1/V) (?V/?P)T The isothermal
compressibility for liquid water is b
4.46555x10-5 atm-1 Why does the equation
defining isothermal compressibility have a minus
sign? Can you separate varibles and integrate
this equation to obtain a function describing how
the volume of a substance will vary with pressure
at constant temperature? A stainless steel bomb
is filled with liquid water at 25.0 oC and 1.000
atm. This bomb is then heated to 50.0 oC. The
volume of the stainless steel bomb is assumed
to remain constant during the heating. What will
be the pressure inside the bomb at 50.0
oC? Use the definitions of coefficient of themal
expansion and isothermal compressibility and the
circle rule (?V/?P)T (?P/?T)V (?T/?V)P -
1 (note how the variables are permuted among the
derivatives in the circle rule) to derive an
equation relating pressure to temperature at
constant volume. You will need the coefficient
of thermal expansion and isothermal
compressibility for liquid water found in the
preceding notes to complete this problem.
12
An important mechanism of weathering occurs when
liquid water that has filled cracks and voids in
rocks freezes and expands. What increase in
pressure in the water filled crack in atmospheres
can be expected when the liquid water filling it
freezes? Take the isothermal compressibility of
ice to be 0.33 GPa-1. At 0.0 ?C the density of
liquid water is 0.9998 g/cm3 and the density of
ice is 0.9168 g/cm3. Assume that the liquid
water is completely confined by the rock and has
no free surface into which to expand.
13
Thermal Behavior of ZrW2O8 Bonus Problem A
Bonus Problem dealing with the Thermal Behavior
of ZrW2O8 can be accessed by clicking the above
link.