LogLinear Modelling modelling frequency data

1
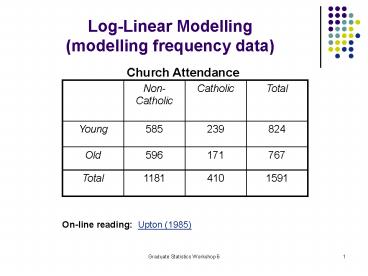
Log-Linear Modelling(modelling frequency data)
Church Attendance
On-line reading Upton (1985)
2
Log-Linear Modelling

• General Model
• Log(F) ? ?1 ?2 . ?n
• Log(F) ß0 ß1 ß2 .. ßn
• negative expected counts cannot occur.
• The expected distribution of the variables is
  Poisson, rather than normal or binomial.
• Model fit Log-Likelihood Chi-square.

3
Logistic versus Log-linear Analysis

• For Log-linear analysis-
• The response variable is categorical (nominal or
  ordinal). For logistic regression it is binomial.
  
• The expected distribution of the categorical
  variables is Poisson. For logistic regression it
  is binomial.
• The model is based on the log, as against the
  logit.
• The model estimates the cell counts in a
  contingency table (not the logit of the response
  variable).

4
Constant Model Constant - Log(F) ?
Log Likelihood Chi-Square 2 x ? observ freq x
ln(observ freq/expect freq) 2 x
585xln(585/397.75) 239xln(239/397.75)
596x(596/397.75) 171xln(171/397.75) 2 x
225.69 (-121.74) 241.03 (-144.35) 401.26
5
Main Effect Model Constant AgeLog(F) ? ?y
?o
Log Likelihood Chi-Square 2 x ? observ freq x
ln(observ freq/expect freq) 2 x
585xln(585/412) 239xln(239/412)
596x(596/383.5) 171xln(171/383.5) 2 x
205.09 (-130.15) (262.78) (-138.11) 399.22
6
Main Effects Model Constant Age
FaithLog(F) ? ?y ?o ?nc ?c
Log Likelihood Chi-Square 9.39
7
Main Effects plus interaction Model(Saturated
Model) Constant age faith
interaction(agefaith)
Log Likelihood Chi-Square 0
8
Fit of the Models
9
SPSS Parameter Estimates for Saturated Model
10
Expected Frequency from Model
Log(Frequency) 5.145 0.334 1.246
(-0.353) Log(Frequency) 6.372 Frequency
AntiLog(6.372) 585
11
Hierarchical Log-Linear Modelling
Religion Age
Attendance Low Medium
High Non-Catholic Young 322 122
141 Non-Catholic Old 250
152 194 Catholic Young 300
124 139 Catholic Old
259 147 188
First order effects (K1) Age
Attendance Second order effects
(K2) ReligionAge AgeAttendance ReligionAtt
endance Third order effects (K3) ReligionAgeA
ttendance
12
Hierarchical Log-Linear Modelling
13
Partial Associations
14
Logarithms Revision

• Log10 - Log base10Log10 (10) 1 101
  10Log10 (100) 2 102 100Log10 (1000) 3
  103 1000
• Hence 10 x 100 1000Log10(10) Log10(100)
  3 Antilog10 (3) 1000
• Ln Loge or Natural log (based upon natural
  constant e)Ln(2.71828) 1 e1
  2.71828Ln(10) 2.3026 e2.3026
  10Antilog(2.3026) 10