CORE MRP II - PowerPoint PPT Presentation
1 / 49
Title: CORE MRP II
1
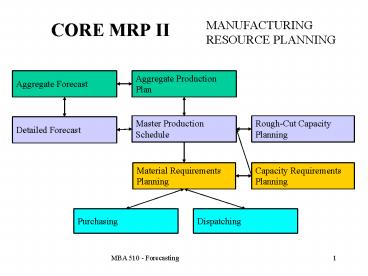
CORE MRP II
MANUFACTURING RESOURCE PLANNING
2
FORECASTING
- Time-series (intrinsic) models
- Time series components
- Base-level forecasting models
- Evaluating forecasting models Mad versus Bias
- Adding trend and seasonality
- Selecting a technique
3
TIME-SERIES (INTRINSIC) FORECASTING MODELS
- Make no assumption about what causes sales
- Identify patterns in past data
- Project those patterns into the future
- Also called autoprojection, intrinsic techniques
4
TIME SERIES COMPONENTS
- Predictable components
- Base level
- Trend
- Seasonality
- Unpredictable components
- Randomness
- All time series techniques work by
- Smoothing randomness out of the past data
- Projecting the leftover pattern implied by these
predictable components into the future
5
SHORT-TERM FORECASTING TECHNIQUES
- Assume absence of trend and seasonality
- Separate base-level (average level) from the
randomness - Some useful models
- Moving Averages
- Exponential Smoothing
6
BASE-LEVEL FORECASTING MODELS
- Assume absence of trend and seasonality
- Separate base-level from randomness
- Ft -- Forecast for period t
- At -- Actual sales for period t
- Bt -- Base level component for period t
- et -- Random element for period t
7
BASE-LEVEL FORECASTING MODELS
- Example tricycle sales at Bikes-R-Us
- Actual July Sales 105
- True Base level for July 100
- Random spike for July 105-100 5
- Assumption At Bt et 105 100 5
- Practical implications for forecasting
- Step 1 Smooth randomness out of At to estimate
Bt - Step 2 Set Ft1 Bt
8
NAÏVE METHOD
- No smoothing of data
- Step 1 Bt At
- Step 2 Ft1 Bt
9
NAÏVE METHOD
- No smoothing of data
- Step 1 Bt At
- Step 2 Ft1 Bt
10
NAÏVE METHOD
- No smoothing of data
- Step 1 Bt At
- Step 2 Ft1 Bt
11
NAÏVE METHOD
- No smoothing of data
- Step 1 Bt At
- Step 2 Ft1 Bt
12
FORECAST EVALUATION
- Need to compare forecast to actual sales
- BIAS
- Too high or to low (on average)?
- Mean Absolute Deviation (MAD)
- Off by how much, per period (on average)?
- Mean Absolute Percentage Error (MAPE)
- A relative measure of MAD
13
FORECAST EVALUATION
- Need to introduce terminology
14
FORECAST EVALUATION
15
FORECAST EVALUATION
16
FORECAST EVALUATION
17
SIMPLE MOVING AVERAGE
- Smoothes out randomness by averaging positive and
negative random elements over several periods - n -- number of periods
- Step 1
- Step 2 Ft1 Bt
18
SIMPLE MOVING AVERAGE
- Smoothes out randomness by averaging positive and
negative random elements over several periods - n -- number of periods
- Step 1
- Step 2 Ft1 Bt
19
SIMPLE MOVING AVERAGE
- Smoothes out randomness by averaging positive and
negative random elements over several periods - n -- number of periods
- Step 1
- Step 2 Ft1 Bt
20
SIMPLE MOVING AVERAGE
- Smoothes out randomness by averaging positive and
negative random elements over several periods - n -- number of periods
- Step 1
- Step 2 Ft1 Bt
21
WEIGHTED MOVING AVERAGE
- Same idea as SMA, but less smoothing more
weight on recent sales data - n -- number of periods
- ai weight applied to period t-i1
- Step 1
- Step 2 Ft1 Bt
22
WEIGHTED MOVING AVERAGE
- Same idea as SMA, but less smoothing more
weight on recent sales data - n -- number of periods
- ai weight applied to period t-i1
- Step 1
- Step 2 Ft1 Bt
23
WEIGHTED MOVING AVERAGE
- Same idea as SMA, but less smoothing more
weight on recent sales data - n -- number of periods
- ai weight applied to period t-i1
- Step 1
- Step 2 Ft1 Bt
24
WEIGHTED MOVING AVERAGE
- Same idea as SMA, but less smoothing more
weight on recent sales data - n -- number of periods
- ai weight applied to period t-i1
- Step 1
- Step 2 Ft1 Bt
25
EXPONENTIAL SMOOTHING (I)
- Simpler equation, equivalent to WMA
- a exponential smoothing parameter (0lt alt1)
- Step 1
- Step 2 Ft1 Bt
26
EXPONENTIAL SMOOTHING (I)
- Simpler equation, equivalent to WMA
- a exponential smoothing parameter (0lt alt1)
- Step 1
- Step 2 Ft1 Bt
27
EXPONENTIAL SMOOTHING (I)
- Simpler equation, equivalent to WMA
- a exponential smoothing parameter (0lt alt1)
- Step 1
- Step 2 Ft1 Bt
28
EXPONENTIAL SMOOTHING (I)
- Simpler equation, equivalent to WMA
- a exponential smoothing parameter (0lt alt1)
- Step 1
- Step 2 Ft1 Bt
29
EXPONENTIAL SMOOTHING (I)
- Simpler equation, equivalent to WMA
- a exponential smoothing parameter (0lt alt1)
- Step 1
- Step 2 Ft1 Bt
30
EXPONENTIAL SMOOTHING (II)
- A higher smoothing parameter means less smoothing
and a more reactive forecast
31
E.S. WITH TREND
- Assumes existence of Trend and Base Level
- Tt Trend component in period t
- a Base-level smoothing parameter (0lt alt1)
- b Trend smoothing parameter (0lt blt1)
- Step 1
- Step 2 Ft1 Bt Tt
32
E.S. WITH TREND
- Assumes existence of Trend and Base Level
- Tt Trend component in period t
- a Base-level smoothing parameter (0lt alt1)
- b Trend smoothing parameter (0lt blt1)
- Step 1
- Step 2 Ft1 Bt Tt
33
E.S. WITH TREND
- Assumes existence of Trend and Base Level
- Tt Trend component in period t
- a Base-level smoothing parameter (0lt alt1)
- b Trend smoothing parameter (0lt blt1)
- Step 1
- Step 2 Ft1 Bt Tt
34
E.S. WITH TREND
- Assumes existence of Trend and Base Level
- Tt Trend component in period t
- a Base-level smoothing parameter (0lt alt1)
- b Trend smoothing parameter (0lt blt1)
- Step 1
- Step 2 Ft1 Bt Tt
35
E.S. WITH TREND
- Assumes existence of Trend and Base Level
- Tt Trend component in period t
- a Base-level smoothing parameter (0lt alt1)
- b Trend smoothing parameter (0lt blt1)
- Step 1
- Step 2 Ft1 Bt Tt
36
E.S. WITH TREND
- Assumes existence of Trend and Base Level
- Tt Trend component in period t
- a Base-level smoothing parameter (0lt alt1)
- b Trend smoothing parameter (0lt blt1)
- Step 1
- Step 2 Ft1 Bt Tt
37
E.S. WITH TREND SEASONS
- St Seasonality component in period t
- L Number of seasons in a year
- g Seasonality smoothing parameter (0lt glt1)
- Step 1
- Step 2 Ft1 (Bt Tt )St-L1
38
E.S. WITH TREND SEASONS
- St Seasonality component in period t
- L Number of seasons in a year
- g Seasonality smoothing parameter (0lt glt1)
- Step 1
- Step 2 Ft1 (Bt Tt )St-L1
39
E.S. WITH TREND SEASONS
- St Seasonality component in period t
- L Number of seasons in a year
- g Seasonality smoothing parameter (0lt glt1)
- Step 1
- Step 2 Ft1 (Bt Tt )St-L1
40
E.S. WITH TREND SEASONS
- St Seasonality component in period t
- L Number of seasons in a year
- g Seasonality smoothing parameter (0lt glt1)
- Step 1
- Step 2 Ft1 (Bt Tt )St-L1
41
E.S. WITH TREND SEASONS
- St Seasonality component in period t
- L Number of seasons in a year
- g Seasonality smoothing parameter (0lt glt1)
- Step 1
- Step 2 Ft1 (Bt Tt )St-L1
42
E.S. WITH TREND SEASONS
- St Seasonality component in period t
- L Number of seasons in a year
- g Seasonality smoothing parameter (0lt glt1)
- Step 1
- Step 2 Ft1 (Bt Tt )St-L1
43
E.S. WITH TREND SEASONS
- St Seasonality component in period t
- L Number of seasons in a year
- g Seasonality smoothing parameter (0lt glt1)
- Step 1
- Step 2 Ft1 (Bt Tt )St-L1
44
E.S. WITH TREND SEASONS
- St Seasonality component in period t
- L Number of seasons in a year
- g Seasonality smoothing parameter (0lt glt1)
- Step 1
- Step 2 Ft1 (Bt Tt )St-L1
45
E.S. WITH TREND SEASONS
- St Seasonality component in period t
- L Number of seasons in a year
- g Seasonality smoothing parameter (0lt glt1)
- Step 1
- Step 2 Ft1 (Bt Tt )St-L1
46
E.S. WITH TREND SEASONS
- St Seasonality component in period t
- L Number of seasons in a year
- g Seasonality smoothing parameter (0lt glt1)
- Step 1
- Step 2 Ft1 (Bt Tt )St-L1
47
E.S. WITH TREND SEASONS
- St Seasonality component in period t
- L Number of seasons in a year
- g Seasonality smoothing parameter (0lt glt1)
- Step 1
- Step 2 Ft1 (Bt Tt )St-L1
48
FORECASTING MORE THAN ONE PERIOD AHEAD
- m periods ahead to be forecast
- Base level forecasts Ftm Bt
- Forecasts with trend Ftm Bt mTt
- Forecasts with seasonality Ftm (Bt mTt
)St-Lm
49
SELECTING A TECHNIQUE
- Ockham's razor -- use the simplest possible model
or theory (William of Ockham, 1300-1349, England) - 1) Determine type of technique which is
appropriate (i.E., Base-level, trend, etc.) - 2) Select a group of competing techniques which
satisfy condition (1) - 3) Select a set of data as a test set
- 4) Simulate forecasts for this set of data using
all techniques from (2) - 5) Pick the technique with the best combination
of MAD/MAPE and Bias