V19 Extreme Pathways

1
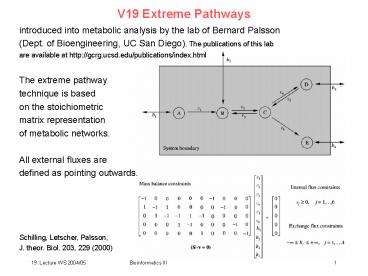
V19 Extreme Pathways
introduced into metabolic analysis by the lab of
Bernard Palsson (Dept. of Bioengineering, UC San
Diego). The publications of this lab are
available at http//gcrg.ucsd.edu/publications/ind
ex.html The extreme pathway technique is
based on the stoichiometric matrix
representation of metabolic networks. All
external fluxes are defined as pointing
outwards. Schilling, Letscher, Palsson, J.
theor. Biol. 203, 229 (2000)
2
Feasible solution set for a metabolic reaction
network
(A) The steady-state operation of the metabolic
network is restricted to the region within a
cone, defined as the feasible set. The feasible
set contains all flux vectors that satisfy the
physicochemical constrains. Thus, the feasible
set defines the capabilities of the metabolic
network. All feasible metabolic flux
distributions lie within the feasible set, and
(B) in the limiting case, where all constraints
on the metabolic network are known, such as the
enzyme kinetics and gene regulation, the feasible
set may be reduced to a single point. This single
point must lie within the feasible set.
Edwards Palsson PNAS 97, 5528 (2000)
3
Extreme Pathways theorem
Theorem. A convex flux cone has a set of
systemically independent generating vectors.
Furthermore, these generating vectors (extremal
rays) are unique up to a multiplication by a
positive scalar. These generating vectors will be
called extreme pathways. (1) The existence of
a systemically independent generating set for a
cone is provided by an algorithm to construct
extreme pathways (see below). (2)
uniqueness? Let p1, ..., pk be a systemically
independent generating set for a cone. Then
follows that if pj c c both cand c are
positive multiples of pj. Schilling, Letscher,
Palsson, J. theor. Biol. 203, 229 (2000)
4
Extreme Pathways uniqueness
To show that this is true, write the two pathways
cand c as non-negative linear combinations of
the extreme pathways Since the pi are
systemically independent, Therefore both cand
c are multiples of pj. If c1, ..., ck was
another set of extreme pathways, this argument
would show that each of the ci must be a positive
multiple of one of the pi. Schilling, Letscher,
Palsson, J. theor. Biol. 203, 229 (2000)
5
Extreme Pathways algorithm - setup
The algorithm to determine the set of extreme
pathways for a reaction network follows the
pinciples of algorithms for finding the extremal
rays/ generating vectors of convex polyhedral
cones. Combine n ? n identity matrix (I) with
the transpose of the stoichiometric matrix ST. I
serves for bookkeeping. Schilling,
Letscher, Palsson, J. theor. Biol. 203, 229 (2000)
S
I
ST
6
separate internal and external fluxes
Examine constraints on each of the exchange
fluxes as given by ?j ? bj ? ?j If the exchange
flux is constrained to be positive ? do
nothing. If the exchange flux is constrained to
be negative ? multiply the corresponding row of
the initial matrix by -1. If the exchange flux is
unconstrained ? move the entire row to a
temporary matrix T(E). This completes the first
tableau T(0). T(0) and T(E) for the example
reaction system are shown on the previous
slide. Each element of this matrices will be
designated Tij. Starting with x 1 and T(0)
T(x-1) the next tableau is generated in the
following way Schilling, Letscher, Palsson, J.
theor. Biol. 203, 229 (2000)
7
idea of algorithm
(1) Identify all metabolites that do not have an
unconstrained exchange flux associated with them.
The total number of such metabolites is denoted
by ?. For the example, this is only the case for
metabolite C (? 1). What is the main idea? -
We want to find balanced extreme pathways that
dont change the concentrations of metabolites
when flux flows through (input fluxes are
channelled to products not to accumulation of
intermediates). - The stochiometrix matrix
describes the coupling of each reaction to
the concentration of metabolites X. - Now we need
to balance combinations of reactions that leave
concentrations unchanged. Pathways applied to
metabolites should not change their
concentrations ? the matrix entries need to be
brought to 0.
Schilling, Letscher, Palsson, J. theor. Biol.
203, 229 (2000)
8
keep pathways that do not change concentrations
of internal metabolites
(2) Begin forming the new matrix T(x) by
copying all rows from T(x 1) which contain a
zero in the column of ST that corresponds to the
first metabolite identified in step 1, denoted
by index c. (Here 3rd column of
ST.) Schilling, Letscher, Palsson, J.
theor. Biol. 203, 229 (2000)
1 -1 1 0 0 0
1 0 -1 1 0 0
1 0 1 -1 0 0
1 0 0 -1 1 0
1 0 0 1 -1 0
1 0 0 -1 0 1
T(0)
T(1)
1 -1 1 0 0 0

9
balance combinations of other pathways
(3) Of the remaining rows in T(x-1) add
together all possible combinations of rows which
contain values of the opposite sign in column c,
such that the addition produces a zero in this
column. Schilling, et al. JTB 203, 229
1 -1 1 0 0 0
1 0 -1 1 0 0
1 0 1 -1 0 0
1 0 0 -1 1 0
1 0 0 1 -1 0
1 0 0 -1 0 1
T(0)
1 0 0 0 0 0 -1 1 0 0 0
0 1 1 0 0 0 0 0 0 0 0
0 1 0 1 0 0 0 -1 0 1 0
0 1 0 0 0 1 0 -1 0 0 1
0 0 1 0 1 0 0 1 0 -1 0
0 0 0 1 1 0 0 0 0 0 0
0 0 0 0 1 1 0 0 0 -1 1
T(1)
10
remove non-orthogonal pathways
(4) For all of the rows added to T(x) in steps 2
and 3 check to make sure that no row exists that
is a non-negative combination of any other sets
of rows in T(x) . One method used is as
follows let A(i) set of column indices j for
with the elements of row i 0. For the example
above Then check to determine if there
exists A(1) 2,3,4,5,6,9,10,11 another row
(h) for which A(i) is a A(2)
1,4,5,6,7,8,9,10,11 subset of A(h). A(3)
1,3,5,6,7,9,11 A(4) 1,3,4,5,7,9,10 If A(i)
? A(h), i ? h A(5) 1,2,3,6,7,8,9,10,11 where A
(6) 1,2,3,4,7,8,9 A(i) j Ti,j 0, 1 ?
j ? (nm) then row i must be eliminated
from T(x) Schilling et al. JTB 203, 229
11
repeat steps for all internal metabolites
(5) With the formation of T(x) complete steps 2
4 for all of the metabolites that do not have an
unconstrained exchange flux operating on the
metabolite, incrementing x by one up to ?. The
final tableau will be T(?). Note that the number
of rows in T (?) will be equal to k, the number
of extreme pathways. Schilling et
al. JTB 203, 229
12
balance external fluxes
(6) Next we append T(E) to the bottom of T(?).
(In the example here ? 1.) This results in the
following tableau Schilling et
al. JTB 203, 229
1 -1 1 0 0 0
1 1 0 0 0 0 0
1 1 0 -1 0 1 0
1 1 0 -1 0 1 0
1 1 0 1 0 -1 0
1 1 0 0 0 0 0
1 1 0 0 0 -1 1
1 -1 0 0 0 0
1 0 -1 0 0 0
1 0 0 0 -1 0
1 0 0 0 0 -1
T(1/E)
13
balance external fluxes
(7) Starting in the n1 column (or the first
non-zero column on the right side), if Ti,(n1)
? 0 then add the corresponding non-zero row from
T(E) to row i so as to produce 0 in the n1-th
column. This is done by simply multiplying the
corresponding row in T(E) by Ti,(n1) and adding
this row to row i . Repeat this procedure for
each of the rows in the upper portion of the
tableau so as to create zeros in the entire upper
portion of the (n1) column. When finished,
remove the row in T(E) corresponding to the
exchange flux for the metabolite just
balanced. Schilling et al. JTB 203, 229
14
balance external fluxes
(8) Follow the same procedure as in step (7) for
each of the columns on the right side of the
tableau containing non-zero entries. (In this
example we need to perform step (7) for every
column except the middle column of the right side
which correponds to metabolite C.) The final
tableau T(final) will contain the transpose of
the matrix P containing the extreme pathways in
place of the original identity matrix. Sc
hilling et al. JTB 203, 229
15
pathway matrix
1 -1 1 0 0 0 0 0 0
1 1 0 0 0 0 0 0
1 1 -1 1 0 0 0 0 0 0
1 1 -1 1 0 0 0 0 0 0
1 1 1 -1 0 0 0 0 0 0
1 1 0 0 0 0 0 0
1 1 -1 1 0 0 0 0 0 0
T(final) PT Schilling et al. JTB
203, 229
v1 v2 v3 v4 v5 v6 b1 b2 b3
b4
p1 p7 p3 p2 p4 p6 p5
1 0 0 0 0 0 -1 1 0 0
0 1 1 0 0 0 0 0 0 0
0 1 0 1 0 0 0 -1 1 0
0 1 0 0 0 1 0 -1 0 1
0 0 1 0 1 0 0 1 -1 0
0 0 0 1 1 0 0 0 0 0
0 0 0 0 1 1 0 0 -1 1
16
Extreme Pathways for model system
2 pathways p6 and p7 are not shown (right below)
because all exchange fluxes with the exterior
are 0. Such pathways have no net overall effect
on the functional capabilities of the
network. They belong to the cycling of reactions
v4/v5 and v2/v3.
Schilling et al. JTB 203, 229
v1 v2 v3 v4 v5 v6 b1 b2 b3
b4
p1 p7 p3 p2 p4 p6 p5
1 0 0 0 0 0 -1 1 0 0
0 1 1 0 0 0 0 0 0 0
0 1 0 1 0 0 0 -1 1 0
0 1 0 0 0 1 0 -1 0 1
0 0 1 0 1 0 0 1 -1 0
0 0 0 1 1 0 0 0 0 0
0 0 0 0 1 1 0 0 -1 1
17
How reactions appear in pathway matrix
In the matrix P of extreme pathways, each column
is an EP and each row corresponds to a reaction
in the network. The numerical value of the i,j-th
element corresponds to the relative flux level
through the i-th reaction in the j-th EP.
Papin, Price, Palsson, Genome Res. 12, 1889
(2002)
18
Properties of pathway matrix
A symmetric Pathway Length Matrix PLM can be
calculated where the values along the diagonal
correspond to the length of the EPs.
The off-diagonal terms of PLM are the number of
reactions that a pair of extreme pathways have in
common.
Papin, Price, Palsson, Genome Res. 12, 1889 (2002)
19
Properties of pathway matrix
One can also compute a reaction participation
matrix PPM from P where the diagonal
correspond to the number of pathways in which the
given reaction participates.
Papin, Price, Palsson, Genome Res. 12, 1889 (2002)
20
EP Analysis of H. pylori and H. influenza
Amino acid synthesis in Heliobacter pylori vs.
Heliobacter influenza studied by EP analysis.
Papin, Price, Palsson, Genome Res. 12, 1889 (2002)
21
Extreme Pathway Analysis
Calculation of EPs for increasingly large
networks is computationally intensive and results
in the generation of large data sets. Even for
integrated genome-scale models for microbes under
simple conditions, EP analysis can generate
thousands of vectors! Interpretation - the
metabolic network of H. influenza has an order of
magnitude larger degree of pathway redundancy
than the metabolic network of H. pylori Found
elsewhere the number of reactions that
participate in EPs that produce a particular
product is poorly correlated to the product yield
and the molecular complexity of the
product. Possible way out?
Papin, Price, Palsson, Genome Res. 12, 1889 (2002)
22
Diagonalisation of pathway matrix?
http//mathworld.wolfram.com
23
Single Value Decomposition of EP matrices
For a given EP matrix P ?? n?p, SVD decomposes P
into 3 matrices
where U ?? n?n is an orthonormal matrix of the
left singular vectors, V ??p?p is an analogous
orthonormal matrix of the right singular vectors,
and ? ??r?r is a diagonal matrix containing the
singular values ?i1..r arranged in descending
order where r is the rank of P. The first r
columns of U and V, referred to as the left and
right singular vectors, or modes, are unique and
form the orthonormal basis for the column space
and row space of P. The singular values are the
square roots of the eigenvalues of PTP. The
magnitude of the singular values in ? indicate
the relative contribution of the singular vectors
in U and V in reconstructing P. E.g. the second
singular value contributes less to the
construction of P than the first singular value
etc.
Price et al. Biophys J 84, 794 (2003)
24
Single Value Decomposition of EP Interpretation
The first mode (as the other modes) corresponds
to a valid biochemical pathway through the
network. The first mode will point into the
portions of the cone with highest density of EPs.
Price et al. Biophys J 84, 794 (2003)
25
SVD applied for Heliobacter systems
Cumulative fractional contributions for the
singular value decomposition of the EP matrices
of H. influenza and H. pylori. This plot
represents the contribution of the first n modes
to the overall description of the system.
Price et al. Biophys J 84, 794 (2003)
26
Summary (extreme pathways)
Extreme pathway analysis provides a
mathematically rigorous way to dissect complex
biochemical networks. The matrix products PT ? P
and PT ? P are useful ways to interpret pathway
lengths and reaction participation. However, the
number of computed vectors may range in the
1000sands. Therefore, meta-methods (e.g.
singular value decomposition) are required that
reduce the dimensionality to a useful number that
can be inspected by humans. Single value
decomposition may be one useful method ... and
there are more to come.
Price et al. Biophys J 84, 794 (2003)
27
Computational metabolomics modelling constraints

• Surviving (expressed) phenotypes must satisfy
  constraints imposed on the molecular functions of
  a cell, e.g. conservation of mass and energy.
• Fundamental approach to understand biological
  systems identify and formulate constraints.
• Important constraints of cellular function
• physico-chemical constraints
• Topological constraints
• Environmental constraints
• Regulatory constraints

Price et al. Nature Rev Microbiol 2, 886 (2004)
28
Physico-chemical constraints
These are hard constraints Conservation of
mass, energy and momentum. Contents of a cell
are densely packed ? viscosity can be 100 1000
times higher than that of water Therefore,
diffusion rates of macromolecules in cells are
slower than in water. Many molecules are
confined inside the semi-permeable membrane ?
high osmolarity. Need to deal with osmotic
pressure (e.g. NaK pumps) Reaction rates are
determined by local concentrations inside
cells Enzyme-turnover numbers are generally less
than 104 s-1. Maximal rates are equal to the
turnover-number multiplied by the enzyme
concentration. Biochemical reactions are driven
by negative free-energy change in forward
direction.
Price et al. Nature Rev Microbiol 2, 886 (2004)
29
Topological constraints
The crowding of molecules inside cells leads to
topological (3D)-constraints that affect both the
form and the function of biological
systems. E.g. the ratio between the number of
tRNAs and the number of ribosomes in an E.coli
cell is about 10. Because there are 43 different
types of tRNA, there is less than one full set of
tRNAs per ribosome ? it may be necessary to
configure the genome so that rare codons are
located close together. E.g. at a pH of 7.6
E.coli typically contains only about 16 H
ions. Remember that H is involved in many
metabolic reactions. Therefore, during each such
reaction, the pH of the cell changes!
Price et al. Nature Rev Microbiol 2, 886 (2004)
30
Environmental constraints
Environmental constraints on cells are time and
condition dependent Nutrient availability, pH,
temperature, osmolarity, availability of electron
acceptors. E.g. Heliobacter pylori lives in the
human stomach at pH1 ? needs to produce NH3 at
a rate that will maintain ist immediate
surrounding at a pH that is sufficiently high to
allow survival. Ammonia is made from elementary
nitrogen ? H. pylori has adapted by using amino
acids instead of carbohydrates as its primary
carbon source.
Price et al. Nature Rev Microbiol 2, 886 (2004)
31
Regulatory constraints
Regulatory constraints are self-imposed by the
organism and are subject to evolutionary change ?
they are no hard constraints. Regulatory
constraints allow the cell to eliminate
suboptimal phenotypic states and to confine
itself to behaviors of increased fitness.
Price et al. Nature Rev Microbiol 2, 886 (2004)
32
Mathematical formation of constraints
There are two fundamental types of constraints
balances and bounds. Balances are constraints
that are associated with conserved quantities as
energy, mass, redox potential, momentum or with
phenomena such as solvent capacity,
electroneutrality and osmotic pressure. Bounds
are constraints that limit numerical ranges of
individual variables and parameters such as
concentrations, fluxes or kinetic
constants. Both bound and balance constraints
limit the allowable functional states of
reconstructed cellular metabolic networks.
Price et al. Nature Rev Microbiol 2, 886 (2004)
33
Genome-scale networks
Price et al. Nature Rev Microbiol 2, 886 (2004)
34
Tools for analyzing network states
The two steps that are used to form a solution
space reconstruction and the imposition of
governing constraints are illustrated in the
centre of the figure. Several methods are being
developed at various laboratories to analyse the
solution space. Ci and Cj concentrations of
compounds i and j EP, extreme pathway vi and
vj fluxes through reactions i and j v1 v3 flux
through reactions 1-3 vnet, net flux through
loop.
Price et al. Nature Rev Microbiol 2, 886 (2004)
35
Determining optimal states
Price et al. Nature Rev Microbiol 2, 886 (2004)
36
Flux dependencies
Price et al. Nature Rev Microbiol 2, 886 (2004)
37
Characterizing the whole solution space
Price et al. Nature Rev Microbiol 2, 886 (2004)
38
Altered solution spaces
Price et al. Nature Rev Microbiol 2, 886 (2004)
39
Additional constraints
Price et al. Nature Rev Microbiol 2, 886 (2004)
40
Outlook

• The research field of computational metabolic
  networks is still in its booming
• starting phase
• current methods are constantly being refined
  (e.g. improved algorithms
• to compute elementary modes, see V21)
• - new types of analysis are constantly being
  introduced.
• The tools seem already valuable enough to be
  applied in biotechnological
• applications.
• Next week
• V20 applications of flux balance analysis
• V21 elementary modes contrasted with extreme
  pathways