What is a graph ? - PowerPoint PPT Presentation
Title:
What is a graph ?
Description:
4. 5. What is a graph ? G=(V,E) V = a set of vertices. E ... adjacency matrix. Representing a graph. adjacency matrix. 1. 2. 3. 4. 5. 0. 0. 0. 0. 1. 0. 0. 1. 1 ... – PowerPoint PPT presentation
Number of Views:12
Avg rating:3.0/5.0
Title: What is a graph ?
1
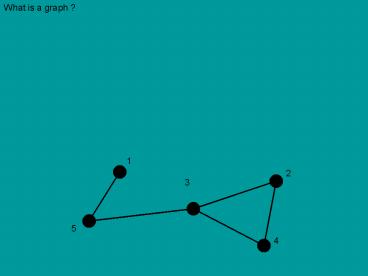
What is a graph ?
1
2
3
5
4
2
What is a graph ?
G(V,E)
V a set of vertices E a set of edges
edge unordered pair of vertices
1
2
3
5
4
3
What is a graph ?
G(V,E)
V 1,2,3,4,5 E 1,5, 3,5, 2,3, 2,4,
3,4
1
2
3
5
4
4
What is a graph ?
G(V,E)
V 1,2,3,4,5 E 1,5, 2,3, 2,4, 3,4
1
2
3
5
4
5
Connectedness
connected
3
1
2
5
4
not connected
3
1
2
5
4
How can we check if a graph is connected?
6
Representing a graph
adjacency matrix
V V symmetric matrix A with Ai,j 1 if
i,j? E Ai,j 0 otherwise
7
Representing a graph
adjacency matrix
3
1
2
5
4
0 0 1 0 1
0 0 1 1 0
1 1 0 1 0
0 1 1 0 0
1 0 0 0 0
space ?(V2)
8
Representing a graph
adjacency matrix
3
1
2
0 0 1 0 1
0 0 1 1 0
1 1 0 1 0
0 1 1 0 0
1 0 0 0 0
5
4
space ?(V2)
is u,v an edge ? ?(?) list neighbors
of v ?(?)
9
Representing a graph
adjacency matrix
3
1
2
0 0 1 0 1
0 0 1 1 0
1 1 0 1 0
0 1 1 0 0
1 0 0 0 0
5
4
space ?(V2)
is u,v an edge ? ?(1) list neighbors
of v ?(n)
10
Representing a graph
adjacency lists
for each vertex v? V linked list of neighbors of v
11
Representing a graph
adjacency lists
3
1
2
5
4
1 3,5 2 3,4 3 1,2,4 4 2,3 5 1
space ?(E)
12
Representing a graph
adjacency lists
3
1
2
1 3,5 2 3,4 3 1,2,4 4 2,3 5 1
5
4
space ?(E)
is u,v an edge ? ?(?) list neighbors
of v ?(?)
13
Representing a graph
adjacency lists
3
1
2
1 3,5 2 3,4 3 1,2,4 4 2,3 5 1
5
4
space ?(E)
is u,v an edge ? ?(min(dv,du)) list
neighbors of v ?(dv)
14
Representing a graph
adjacency lists
space ?(E)
1 3,5 2 3,4 3 1,2,4 4 2,3 5 1
is u,v in E ? ?(mindu,dv) neigbors
of v ? ?(dv)
adjacency matrix
space ?(V2)
0 0 1 0 1
0 0 1 1 0
1 1 0 1 0
0 1 1 0 0
1 0 0 0 0
is u,v in E ? ?(1) neigbors of v ?
?(n)
15
Counting connected components
How can we check if a graph is connected?
INPUT graph G given by adjacency list
OUTPUT number of components of G
16
BFS (G,v)
G undirected graph, V1,...,n seenv false
for all v ? V Qqueue (FIFO)
seenv ? true enqueue(Q,v) while Q
not empty do w ? dequeue(Q) for
each neighbor u of w if not seenu
then seenu ? true
enqueue(Q,u)
17
Counting connected components
C ? 0 for all v ? V do seenv ? false
for all v ? V do if not seenv then
C BFS(G,v) output G has C
connected components
18
DFS
G undirected graph, V1,...,n visitedv
false for all v ? V
explore(G,v) visitedv ? true for each
neighbor u of v if not visited(u) then
explore(G,u)
19
DFS
G undirected graph, V1,...,n visitedv
false for all v ? V
explore(G,v) visitedv ? true prev ?
clock clock for each neighbor u of v
if not visited(u) then explore(G,u) postv
? clock clock
20
DFS
explore(G,v) visitedv ? true prev ?
clock clock for each neighbor u of v
if not visited(u) then explore(G,u) postv
? clock clock
vertex ? Iv prev,postv
interval property for u,v? V either
Iv and Iu are disjoint, or one is
contained in the other
21
DFS
explore(G,v) visitedv ? true prev ?
clock clock for each neighbor u of v
if not visited(u) then explore(G,u) postv
? clock clock
A
B
D
C
22
DFS
explore(G,v) visitedv ? true prev ?
clock clock for each neighbor u of v
if not visited(u) then explore(G,u) postv
? clock clock
A
tree edges
B
D
C
23
Digraphs (directed graphs)
G(V,E)
V a set of vertices E a set of edges
edge ordered pair of vertices
(u,v)
v
u
24
Digraphs (directed graphs)
adjacency lists
for each vertex v? V linked list of out-neighbors
of v
adjacency matrix
V V matrix A with Ai,j 1 if (i,j)? E
Ai,j 0 otherwise
25
Digraphs (directed graphs)
a path sequence of vertices v1,v2,...,vk
such that (v1,v2)? E, ... , (vk-1,vk)? E
26
DAGs (acyclic digraphs)
a cycle sequence of vertices v1,v2,...,vk
such that (v1,v2)? E, ... ,
(vk-1,vk),(vk,v1)? E
DAG digraph with no cycle
27
Topological sort (linearization)
INPUT DAG G given by adjacency list
OUTPUT ordering of vertices such that
edges go forward
28
DFS on digraphs
G digraph, V1,...,n visitedv false for
all v ? V
explore(G,v) visitedv ? true prev ?
clock clock for each out-neighbor u of v
if not visited(u) then explore(G,u)
postv ? clock clock
29
DFS on digraphs
A
B
D
C
30
DFS on digraphs
A
root
B
D
C
descendant, ancestor child, parent
31
DFS on digraphs
A
tree edge
B
D
C
32
DFS on digraphs
A
tree edge
B
D
C
33
DFS on digraphs
back edge
A
tree edge
B
D
C
34
DFS on digraphs
back edge
A
tree edge
B
D
C
cross edge
35
DFS on digraphs
back edge
A
tree edge
B
forward edge
D
C
cross edge
36
Relationships between the intervals?
back edge
A
tree edge
B
forward edge
D
C
cross edge
37
Topological sort using DFS
Lemma digraph is a DAG if and only
if DFS has a back edge.
38
Topological sort using DFS
Lemma digraph is a DAG if and only
if DFS has a back edge.
Lemma in a DAG every edge goes to a
vertex with lower post
explore(G,v) visitedv ? true prev ?
clock clock for each neighbor u of v
if not visited(u) then explore(G,u) postv
? clock clock
39
(strong) connectedness
a digraph G is strongly connected if for every
u,v? V there exists a path from u to v in G
40
(strong) connectedness
How to check if a digraph is strongly connected?
41
(strong) connectedness
How to check if a digraph is strongly connected?
for every u?V do DFS(G,u) check if every
v?V was visited
42
(strong) connectedness
How to check if a digraph is strongly connected?
pick some u?V DFS(G,u) check if every v?V was
visited DFS(reverse(G),u) check if every v?V was
visited
43
Strongly connected components
DAG of strongly connected components
44
Strongly connected components
Lemma G and reverse(G) have the same strongly
connected components.
45
Strongly connected components
DAG of strongly connected components
46
Strongly connected components
for all v? V do colorv? white for all v? V do
if colorvwhite then
DFS(reverse(G),v) DFS(G,u)
(vertices in order post)