Introduction to hypothesis testing

1
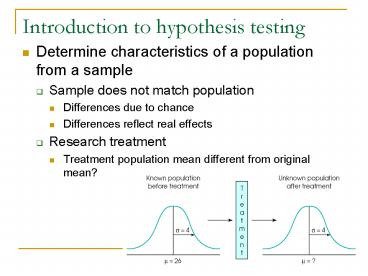
Introduction to hypothesis testing

• Determine characteristics of a population from a
  sample
• Sample does not match population
• Differences due to chance
• Differences reflect real effects
• Research treatment
• Treatment population mean different from original
  mean?

2
Logic of hypothesis testing State hypotheses

• H0 the null hypothesis
• No effect of treatment
• Any differences due to sampling error
• H1 the alternative or scientific hypothesis
• Treatment had an effect
• Real differences
• Hypotheses contradictory and mutually exclusive
• H0 states a specific value for population
  parameter
• E.g., µtreatment µpopulation
• How likely are the results if Ho is true?
• If unlikely H0 is probably not true

3
Logic of hypothesis testing

• Set criteria for decision
• How unlikely?
• Collect sample
• Observe sample statistic
• Evaluate sample statistic consistency with the
  population parameter given by the H0
• Probability that the H0 is true
• Very unlikely reject the H0
• Reasonable chance H0 truefail to reject H0
• Assume H0 true
• Argument by contradiction

4
Evaluating the H0

• Alpha a or significance level
• Traditional levels
• .05 or .01
• p value p(H0 true)
• Critical regioncritical values
• Choice of .05 or .01how important to be certain

5
Example using coin tossing

• H0 Coin is fair and the P(head) .5
• H1 Coin is not fair and P(head) ? .5
• Sample 10 heads in a row
• Set a at .05
• P(10 heads) 1/2 X 1/2 X 1/2 X...X ½ 1/210
  .000976
• Based on assumption H0 true

6
Errors

• Type I or a errors consist of rejecting the H0
  when the H0 is true
• p (type I error) a
• Type II or ß errors consist of failing to reject
  the H0 when the H0 is false
• p (type II error) ß

7
z test

• µ 1,000, s 500
• M 3,000, n 20
• H0 ? 1,000
• H1? ? 1,000
• a .05

8

• If M 1,050
• Area in tail for z (0.45) .3264, p 2.3264
  0.6528
• P gt .05, fail to reject H0

9
Steps

• State H0 and H1
• Set a
• Determine critical value and region
• Determine
• Evaluate H0, z exceed critical value

10
Another example

• ? 4, s .45
• M 3.85, n 25
• H0 ? 4, H1 ? ? 4
• ? .01
• Critical z 2.57583
• Z 1.667, pgt.01
• Retain the H0

11
Basic Elements

• Hypothesized population parameter H0
• Sample statistic
• Estimate of error/chance, standard error
• Alpha level ?
• ? .05 the test statistic critical value will
  be around 2.00
• ? .01 the test statistic critical value will
  be around 2.50
• ? .001 the test statistic critical value will
  be around 3.00

12

• Reporting
• Significant test statistic value, p lt alpha
• z 2.50, p lt .05
• Not significant test statistic value, p gt alpha
  or n.s.
• z 1.22, p gt.05
• Precise p from computer
• Assumptions
• Random sample
• Independent observations
• ? unchanged by the treatment, constant added to
  scores

13
Directional versus nondirectional tests
Onetailed and twotailed tests

• Two tailed, difference regardless of direction
• H0 ? 100, H1 ? ? 100
• One tailed, specific direction
• H0 ? 1,000, H1 ? gt 1,000
• a .05
• z two tailed 1.96
• z one tailed 1.65

14
Concerns

• Criticisms
• All or none 1.95 versus 1.97
• H0 artificial
• Ignores magnitude of effect
• M 3.9. The ? .45.
• H0 ? 4, H1 ? ? 4
• ? .01, z 2.58
• n 25
• z 1.11, p gt .01

15

• n 900
• z 6.67, p lt .01
• Statistical versus real world significance
• Effect size

16

• Mean 3.5
• Small 0 lt d lt 0.2 (.25)
• Medium 0.2 lt d lt 0.8 (.5)
• Large effect d gt 0.8 (1.25)

17
Statistical Power

• Ability to reject false H0
• Power depends on
• Magnitude of treatment effect
• Alpha level
• Sample size
• One tailed versus two tailed test
• Magnitude of treatment effect
• Small .25 s
• Medium .75 s
• Large 1.25 s

18
Effect Magnitude and Power

• µ 100, sM 10, Real µ 110 (actual population
  µ), a .05
• Critical value assuming H0 is true
• .1685 above 119.6

19

• µ 100, sM 10, real µ 135, a .05
• Critical value
• 
  .
• .9382 above 119.6

20
Sample Size and Power

• µ 100, s 10, real µ 110, n 4, sM 5, a
  .05
• Critical value
• 
  .5160 above 109.8

21
Sample Size and Power

• µ 100, s 10, real µ 110, n 25, sM 2, a
  .05
• Critical value
• 
  .9987 above 103.92

22
Alpha, Beta, and Power

• µ 100, s 5, a .05, z 1.96, M 110
• Critical value 109.8
• µ 100, s 5, a .01, z 2.575
• Critical value 114.9
• More stringent a (.01)
• Lower p (Type I error)
• Higher p (Type II error)
• Lower power

23
One versus Two Tailed

• Two tailed, µ 100, s 5, a .05, z 1.96,
  Real µ 110
• Critical value 109.8
• One tailed, µ 100, s 5, a .05, z 1.65,
  Real µ 110
• Critical value 108.25

24
Effect Size, Power, and n
25
Interval Estimation

• Critical Value of Z 1.96
• M 50, sM 4
• Hypothesized µ lt 42.16 or µ gt 57.84 reject H0