The Border Problem

1
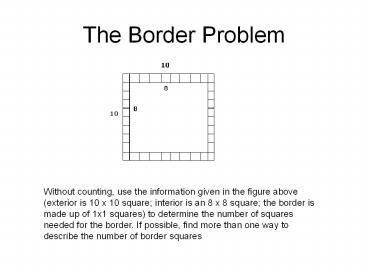
The Border Problem
Without counting, use the information given in
the figure above (exterior is 10 x 10 square
interior is an 8 x 8 square the border is made
up of 1x1 squares) to determine the number of
squares needed for the border. If possible, find
more than one way to describe the number of
border squares
2
Numerical Expressions Geometric Explanation
102-82 Area of large (exterior) square minus area of the small (interior) square.
4(10)-4 There are four sides of length 10 minus the four overlapping squares.
2(10)2(8) The are two sides of length 10 and two sides of length 8. Notice that for the two sides of length 10 that all corners of the border are counted.
4(8)4 There are four sides of length 8. We must add 4 for the four corners.
4(9) There are four sides of length 9. Each side includes a different corner. Each of the four corners is counted exactly once.
10998 There is one side of length 10 (which includes two corners). There are two sides of length 9 (which includes a total of 2 corners). There is a side of length 8 (which includes no corners)
3
Video Discussion

• Why without talking?
• Why without writing?
• Why without counting one by one?
• Why not give them each a grid to facilitate their
  thinking?
• Why did the teacher act as the recorder for the
  arithmetic expressions?

Boaler, J. Humphreys, C. (2005). Building on
student ideas The border problem, part I.
Connecting mathematical ideas Middle school
video cases to support teaching and learning
(pp.13-39). New Hampshire Heineman Publications.
4

• What about a 6 in by 6 in grid?
• What about a 15 in by 15 in grid?
• What about a 253 in by 253 in grid?
• What about an n inch by n inch grid?
• Create a verbal representation
• Use the verbal representation to introduce the
  notion of variable
• If n represents the number of unit squares on one
  side, give an algebraic expression for the number
  of unit squares in the border.
• Develop understanding of function, variables
  (independent and dependent) and graphing.