Age Structure

1
Age Structure
2
Lecture Goals

• Review life tables (types, data sources, etc.)
• Develop population projections from life tables
• As a consequence of age specific birth and death
• Express population projection in matrix form
• What is the matrix?
• Examine properties of matrix population models

3
Age Structure A Review of Life Tables
X lx mx 0 1.00 0 1 0.10 5 2 0.05 2 . . . . . .
X age lx survival to age X mx mean
offspring at age X
px probability of surviving from age X to X1
p0 l1/l0 0.10/1.00 0.1
p1 l2/l1 0.05/0.10 0.5
4
Types of life tables from data sources
5
Review of Useful Life Table Calculations
R0 average lifetime reproduction S lxmx
6
Reproductive Value for Red Deer (Clutton-Brock
1984)
7
Life Tables Can Also Be Used To Predict Future
Population Size
X2
?
X1
X0
8
Order of Birth and Survival in Following
Development
Age 0
Age 1
Age 2
Birth(m0)
Birth(m1)
Birth(m2)
Survival (p0)
Survival (p1)
Survival (p2)
9
Underlying questions/calculations
X lx mx px 0 1.00 0 0.1 1 0.10 5 0.5 2 0.05 2 0.0

• If we start with
• 100 age 0
• 10 age 1
• 5 age 2

Next year
How many offspring? How many age 1? How many age
2?
1000 105 52 60 1000.1 100 50
10 1000 100.5 50 5
10
The formulae
Numbers of each class (1,2,3) are N0, N1, N2
t 1
t
N0 m0N0 m1N1 m2N2 N1 p0N0 0N1
0N2 N2 0N0 p1N1 0N2
NOTE the subscript represents age, not time
11
The formulae Matrix Notation
m0 m1 m2 p0 0 0 0 p1 0
N0 N1 N2

N0' N1' N2'
Leslie MatrixTransition Matrix
population vectors
12
Just Enough About Matrices
m0 m1 m2 p0 0 0 0 p1 0
N0 N1 N2
N0' N1' N2'

T x N N'

• matrices and vectors are often represented by
  bold faced type
• Index order of elements is row,column
• a1,2 is in row 1, column 2
• multiplication order is important
• T x N ? N x T

13
N0 N1 N2
For any N0, N1,
T x N N', T x N' N'', T x N'' N''' ,
N

Eventually, a stable age structure occurs.
N2
N0
N1
are constant as the population changes.

,
,
SNi
SNi
SNi
14
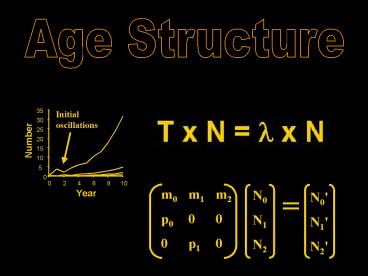
Graphically, we see the age structures stabilize
35
Initialoscillations
30
25
Number
Total Number
20
15
10
???
5
0
0
2
4
6
8
10
Year
Year
(4 lines 4 age classes)
What does this population pattern resemble?
15
Regardless of the (non-zero) starting value,
eventually the population attains a stable age
structure, and then
T x N l x N
Where l is the parameter from the geometric
population growth model. Mathematically l is the
dominant latent root or dominant eigenvalue of T.
We could also use Nt l Nt1 and the stable age
structure to get the same result.
16
When would it be necessary to use a population
matrix model instead of the much simpler
geometric model of population growth?

• Unstable age structure
• after perturbation (invasion, fire, etc.)

Will a static life table be adequate to examine a
population limited by density dependent factors?
No - it follows geometric, unlimited growth
17
Variable Parameters in Leslie Matrices? Building
more complex models

• Let some or all mx and px be represented as a
  function of Nx or SNi.
• represents density dependence
• mx decline with numbers
• px decline with numbers
• General Leslie matrix results no longer apply
• Age structured model
• not solvable by matrix math
• programmable (simulation)

18
Example of Poa annua (Annual Bluegrass)
19
(No Transcript)
20
Executing the Simulation Model

• population stabilizes (intraspecific
  competition)
• age structure stabilizes(similar to cases
  without intraspecific competition)

21
If you were given all of the information required
for the Poa model, how would you calculate the
net reproductive rate (R or l)?