Forces

1

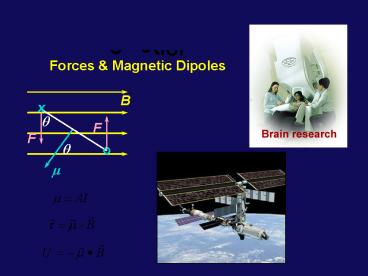
• Forces Magnetic Dipoles

2
Today...

• Application of equation for trajectory of charged
  particle in a constant magnetic field Mass
  Spectrometer
• Magnetic Force on a current-carrying wire
• Current Loops
• Magnetic Dipole Moment
• Torque (when in constant B field) ? Motors
• Potential Energy (when in constant B field)
• Appendix Nuclear Magnetic Resonance Imaging
• Solar Flare/Aurora
  Borealis Pictures

3
Last Time

• Units of B are Tesla
• 1 Tesla 104 Gauss
• Earths B-field 0.5 G

• Several applications of this
• Thomson (1897) measures q/m ratio for cathode
  rays
• All have same q/m ratio, for any material source
• Electrons are a fundamental constituent of all
  matter!
• Accelerators for particle physics
• One can easily show that the time to make an
  orbit does not depend on the size of the orbit,
  or the velocity of the particle
• Cyclotron

4
Mass Spectrometer

• Measure m/q to identify substances

• Electrostatically accelerated electrons knock
  electron(s) off the atom ? positive ion (qe)
• Accelerate the ion in a known potential UqV
• Pass the ions through a known B field
• Deflection depends on mass Lighter deflects
  more, heavier less

5
Mass Spectrometer, cont.

• Electrically detect the ions which made it
  through
• Change B (or V) and try again

Applications Paleoceanography Determine
relative abundances of isotopes (they decay at
different rates ? geological age) Space
exploration Determine whats on the moon, Mars,
etc. Check for spacecraft leaks. Detect chemical
and biol. weapons (nerve gas, anthrax, etc.).
See http//www.colby.edu/chemistry/OChem/DEMOS/Mas
sSpec.html
6
Yet another example

• Measuring curvature of charged particle in
  magnetic field is usual method for determining
  momentum of particle in modern experiments e.g.

B
e
e-
End view B into screen
7
Magnetic Force on a Current

• Consider a current-carrying wire in the
• presence of a magnetic field B.
• There will be a force on each of the charges
  moving in the wire. What will be the total force
• dF on a length dl of the wire?
• Suppose current is made up of n charges/volume
  each carrying charge q and moving with velocity v
  through a wire of cross-section A.

N
S
8
Magnetic Force on a Current Loop

• Consider loop in magnetic field as on right If
  field is to plane of loop, the net force on
  loop is 0!

9
Preflight 13
A square loop of wire is carrying current in the
counterclockwise direction. There is a horizontal
uniform magnetic field pointing to the right.
2) What is the force on section a-b of the loop?
a) zero b) out of the page
c) into the page 3) What is the force on
section b-c of the loop? a) zero
b) out of the page c) into the page 4)
What is the net force on the loop? a)
zero b) out of the page c) into
the page
ab Fab 0 Fcd since the wire is parallel to
B.
bc Fbc ILB RHR I is up, B is to the right,
so F points into the screen.
10
Lecture 13, Act 1

• A current I flows in a wire which is formed in
  the shape of an isosceles right triangle as
  shown. A constant magnetic field exists in the
  -z direction.
• What is Fy, net force on the wire in the
  y-direction?

11
Lecture 13, Act 1

• A current I flows in a wire which is formed in
  the shape of an isosceles right triangle as
  shown. A constant magnetic field exists in the
  -z direction.
• What is Fy, net force on the wire in the
  y-direction?

There is never a net force on a loop in a uniform
field!
12
Calculation of Torque

• Suppose the coil has width w (the side we see)
  and length L (into the screen). The torque is
  given by

• Note if loop B, sinq 0 Þ t 0
• maximum t occurs when loop parallel to B

13
Magnetic Dipole Moment

• We can define the magnetic dipole moment of a
  current loop as follows

• direction to plane of the loop in the
  direction the thumb of right hand points if
  fingers curl in the direction of current.

14
Bar Magnet Analogy

• You can think of a magnetic dipole moment as a
  bar magnet

• In a magnetic field they both experience a torque
  trying to line them up with the field
• As you increase I of the loop ? stronger bar
  magnet
• N loops ? N bar magnets
• We will see next lecture that such a current loop
  does produce magnetic fields, similar to a bar
  magnet. In fact, atomic scale current loops were
  once thought to completely explain magnetic
  materials (in some sense they still are!).

15
Potential Energy of Dipole

• Work must be done to change the orientation of a
  dipole (current loop) in the presence of a
  magnetic field.

16
Potential Energy of Dipole
t 0 U -mB
t 0 U mB
U 0
17
Preflight 13
Two current carrying loops are oriented in a
uniform magnetic field. The loops are nearly
identical, except the direction of current is
reversed.
8) What direction is the torque on loop 1?
a) clockwise b) counter-clockwise
c) zero
Loop 1 m points to the left, so the angle
between m and B is equal to 180º, hence t 0.
9) How does the torque on the two loops compare?
a) t1 gt t2 b) t1 t2
c) t1 lt t2
Loop 2 m points to the right, so the angle
between m and B is equal to 0º, hence t 0.
10) Which loop occupies a potential energy
minimum, and is therefore stable?
a) loop 1 b) loop 2
c) the same
18
Applications Galvanometers(Dial Meters)
We have seen that a magnet can exert a torque on
a loop of current aligns the loops dipole
moment with the field.

• In this picture the loop (and hence the needle)
  wants to rotate clockwise
• The spring produces a torque in the opposite
  direction
• The needle will sit at its equilibrium position

This is how almost all dial meters
workvoltmeters, ammeters, speedometers, RPMs,
etc.
19
Motors
Slightly tip the loop ?Restoring force from
the magnetic torque ?Oscillations Now turn
the current off, just as the loops µ is aligned
with B ?Loop coasts around until its µ is
antialigned with B Turn current back on
?Magnetic torque gives another kick to the loop
?Continuous rotation in steady state
20
Motors, continued

• Even better
• ?Have the current change directions every half
  rotation
• ?Torque acts the entire time
• Two ways to change current in loop
• Use a fixed voltage, but change the circuit
  (e.g., break connection every half cycle
• ? DC motors
• 2. Keep the current fixed, oscillate the source
  voltage
• ?AC motors

21
Lecture 13, Act 2

• How can we increase the speed (rpm) of a DC motor?

22
Lecture 13, Act 2

• How can we increase the speed (rpm) of a DC motor?

All of the above, though for variable speed
motors, it is always the current that is adjusted.
23
Example Loop in a B-Field
A circular loop has radius R 5 cm and carries
current I 2 A in the counterclockwise
direction. A magnetic field B 0.5 T exists in
the negative z-direction. The loop is at an
angle q 30? to the xy-plane.
What is the magnetic moment m of the loop?
m p r2 I .0157 Am2
z
m
B
q
X
y
x
24
Electric Dipole Analogy
25
Preflight 13
A square loop of wire is carrying current in the
counterclockwise direction. There is a horizontal
uniform magnetic field pointing to the right.
6) What is the net torque on the loop? a) zero
b) up c) down d) out of the page
e) into the page
26
Summary

• Mass Spectrometer
• Force due to B on I
• Magnetic dipole
• torque
• potential energy
• Applications dials, motors, NMR,
• Next time calculating B-fields from currents

27
MRI (Magnetic Resonance Imaging) NMR
(Nuclear Magnetic Resonance)MRI invented by
UIUC Chem. Prof. Paul Lauterbur,who shared 2003
Nobel Prize in Medicine
A single proton (like the one in every hydrogen
atom) has a charge (e) and an intrinsic
angular momentum (spin). If we (naively)
imagine the charge circulating in a loop ?
magnetic dipole moment µ.
28
MRI / NMR Example
B 1 Tesla (104 Gauss) (note this is a big
field!)
µproton 1.4110-26 Am2
In QM, you will learn that photon energy
frequency Plancks constant
29
MRI / NMR continued
If we bathe the protons in radio waves at this
frequency, the protons can flip back and forth.
If we detect this flipping ? hydrogen! The
presence of other molecules can partially shield
the applied B, thus changing the resonant
frequency (chemical shift). Looking at what the
resonant frequency is ? what molecules are
nearby. Finally, because , if
we put a strong magnetic field gradient across
the sample, we can look at individual slices,
with millimeter spatial resolution.
30
See it in action!
Thanks to
31
Solar Flare/Aurora Borealis links
http//cfa-www.harvard.edu/press/soolar_flare.mov
http//science.nasa.gov/spaceweather/aurora/galler
y_01oct03_page2.html