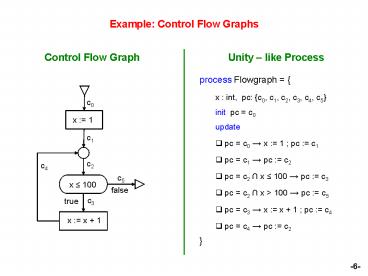
Example: Control Flow Graphs

1
Example Control Flow Graphs
Control Flow Graph
Unity like Process
-6-
2
Example Mutual Exclusion
P P0 P1 P0
P m cobegin P0 P1 coend m P0 l0
while true do nc0 wait (turn 0) cr0
turn 1 l0

• turn 0,1 , pc0 nc0, cr0
• init pc0 nc0
• update
• pc0 nc0 n turn 0 ? pc0 cr0
• pc0 nc0 n turn 1 ? pc0 nc0
• pc0 cr0 ? turn 1 pc0 nc0

P1 l1 while true do nc1 wait (turn
1) cr1 turn 0 l1
P1

• turn 0,1 , pc1 nc1, cr1
• init pc1 nc1
• update
• pc1 nc1 n turn 1 ? pc1 cr1
• pc1 nc1 n turn 0 ? pc1 nc1
• pc1 cr1 ? turn 0 pc1 nc1

Pseudo - code
-7-
3
Example Mutual Exclusion Expanded
process P

• turn 0,1 , pc0 nc0, cr0 , pc1 nc1,
  cr1
• init pc0 nc0 n pc1 nc1
• update
• pc0 nc0 n turn 0 ? pc0 cr0
• pc0 nc0 n turn 1 ? pc0 nc0
• pc0 cr0 ? turn 1 pc0 nc0
• pc1 nc1 n turn 1 ? pc1 cr1
• pc1 nc1 n turn 0 ? pc1 nc1
• pc1 cr1 ? turn 0 pc1 nc1

-8-
4
Example Transition Relation
Semantics
Unity like Process
type arcs c0, c1, c2, c3, c4, c5 process
Flowgraph

• x int, pc arcs
• init pc c0
• update
• pc c0 ? x 1 pc c1
• pc c1 ? pc c2
• pc c2 n x 100 ? pc c3
• pc c2 n x gt 100 ? pc c5
• pc c3 ? x x 1 pc c4
• pc c4 ? pc c2

-9-
5
Example Predicate Transformers
-10-
6
Abstract Semantics of Programs
Abstract State Graphs S (Q,vTi, I)
state graph of the program QA a lattice of
abstract states a P(Q) ? QA a(?(q)) q ?
QA ? P(Q) f -gt ?(a(f))
A Galois connection
given ? ? a(f) ? q ? QA f gt ?(q)
Consequence every concrete execution is
represented by at least one abstract
-11-
7
Abstract State Lattice
Main idea Given f1, .. , fl predicates on
vars of concrete P. B1, .., Bl
boolean variables (all concrete states that
satisfy fi)
Abstract states set of predicates over B1, ..,
Bl (QA).
Monomial on B1, .. , Bl conjunction of Bis and
Bis (at most once)
Theorem The set M of monomials on B1 .. Bl
forms - complete lattice and (a ?) Galois
connection
-12-
8
Abstract Transitions
Main idea Ti A (expA) a(postTi (?(expA)))
Ti A
Problem difficult to compute.
expA
a( postTi ( ?(expA)))
?
a
Ti
Ti A (expA) a(postTi (?(expA)))
?(expA)
postTi (?(expA))
Use monomial approximation a of a. Has following
form
By using (2.1) and (2.2) (3.1) Bj if
expAf?/ B? ? qj -gt fj assi(x?)/ x?
-13-
9
Abstract Successors
Computing abstract successors check validity of
implications (3) - use a decision procedure
(DP) - automatic theorem prover implementing
such DPs. ? for all i ? 1, .. , l . prove (
3.0 3.1 3.2 )
Imposibility of proving (3) - postTi
(expAf?/ B? ) intersects both fj and fj -
abstract expA too big ? cut in smaller pieces -
because of monomials - abstract state space is
too rough. - applied proof strategy is not
powerful enough
Abstract initial state I A a(init) - in
most practical cases, defines one value for most
variables. - can be computed by evaluating fi
-14-