Lecture 8' Matrices

1
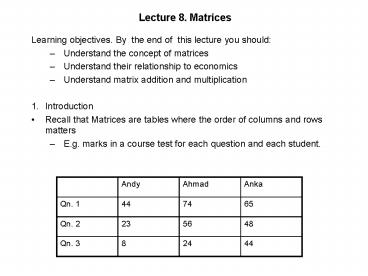
Lecture 8. Matrices

• Learning objectives. By the end of this lecture
  you should
• Understand the concept of matrices
• Understand their relationship to economics
• Understand matrix addition and multiplication
• Introduction
• Recall that Matrices are tables where the order
  of columns and rows matters
• E.g. marks in a course test for each question and
  each student.

2
2. Some common types of matrices in applied
economics.

• Storing data
• Input-output
• Transition matrices. (U unemployed, E
  employed, prob. probability)

3
3. Definitions.

• Dimensions of a matrix.
• The number of rows times the number of columns.
• Example
• A is a 2 x 5 matrix
• B is 5x2 matrix

4
Definitions.

• Sometimes we wish to refer to individual elements
  in a matrix.
• E.g. the number in the third row, second column.
  We use the notation aij (or bij etc.) to indicate
  this.
• i refers to the row
• j refers to the column
• Example
• a13 3
• a21 7
• What is b21

5
3. Definitions

• The null matrix or zero matrix is a matrix
  consisting entirely of zeros.
• A square matrix is one where the number of rows
  equals the number of columns i.e. nxn
• For a square matrix, the leading diagonal is all
  the elements aij where ij.
• The identity matrix is a square matrix consisting
  of zeros except for the leading diagonal which
  consists of 1s
• We write I for the identity matrix. If we wish to
  identify its size we write In

6
4. Mini quiz

• What are the dimensions of A
• What is a21?
• Is B a square matrix?
• What is the largest element on the leading
  diagonal of B?
• What is the value of the largest element on the
  leading diagonal of B?

7
5. More Definitions

• The transpose of a matrix A is obtained by
  swapping aij for aji for all i and j in other
  words by turning rows into columns and vice
  versa. We write the transpose as A or AT.
• A symmetric matrix is one where A A.
• A positive matrix is one where none of the
  elements are negative. A strictly positive matrix
  is one where all of the elements are strictly
  positive , the leading diagonal is all the
  elements aij where ij.
• is symmetric and strictly positive.

8
5. More Definitions

• A negative matrix is one where none of the
  elements are positive. A strictly negative matrix
  is one where all of the elements are strictly
  negative,
• C is strictly positive and symmetric B is
  negative A is neither positive nor negative.

9
6. some rules.

• 1. Adding matrices.
• You can only add two matrices if they have the
  same dimensions.
• e.g. you cannot add A and B
• To add, add each element from the corresponding
  place in the matrices. i.e. if A and B are mxn
  matrices, then AB is the mxn matrix where
• cij aijbij for i 1,..,m and j 1,,n.

10
Multiplying by a scalar.

• When you multiply by a scalar (e.g. 3, 23.1 or
  -2), then you multiply each element of the matrix
  by that scalar.
• Example 1 what is 4A if
• Example 2 what is xB if

11
Summary.

• 11 Definitions you should now memorise
• Matrix dimensions, null matrix, identity matrix,
  transpose, symmetric matrix, square matrix,
  leading diagonal, positive, strictly positive,
  negative and strictly negative matrices.
• 4 skills you should be able to do
• Add two nxm matrices
• Multiply a matrix by a scalar
• Transpose a matrix.
• Identify the element aij in any matrix.