Line Clipping

1
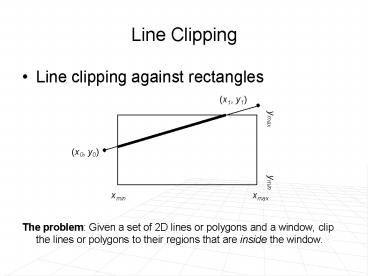
Line Clipping

• Line clipping against rectangles
• The problem Given a set of 2D lines or polygons
  and a window, clip the lines or polygons to their
  regions that are inside the window.

2
Motivations

• Efficiency
• Display in portion of a screen
• Occlusions

Clip rectangle
3
Clipping is tricky!
4
Simple Cases

• If x0 lt xmin and x1 lt xmin
• or x0 gt xmax and x1 gt xmax
• or y0 lt ymin and y1 lt ymin
• or y0 gt ymax and y1 gt ymax
• trivial rejection.
• If xmin x xmax
• and ymin y ymax
• trivially accepted.

5
The Cohen-Sutherland Line-Clipping Algorithm

• Region and outcodes

First bit above top edge y gt ymax Second bit
below bottom edge y lt ymin Third bit to right
of right edge x gt xmax Fourth bit to left of
left edge x lt xmin
6
The C-S Line-Clipping Algorithm (cont.)

• Checking for trivial acceptance or rejection
  using outcodes
• 1). Each endpoint of a line segment is assigned
  an outcode
• 2). If both 4-bit codes are zero, the line can be
  trivially accepted
• 3). A logical and is performed on both outcodes
• 4). If the result is nonzero, the line can be
  trivially rejected.

7
Steps for Cohen-Sutherland Algorithm

1. End-points pairs are checked for trivial
   acceptance or rejection using outcode
2. If not trivially accepted or rejected, divide the
   line segment into two at a clip edge
3. Iteratively clipped by test trivial-acceptance or
   trivial-rejection, and divided into two segments
   until completely inside or trivial-rejection.

8
Polygon Clipping

• Sutherland-Hodgeman algorithm (A
  divide-and-conquer strategy)
• Polygons can be clipped against each edge of the
  window one at a time. Edge intersections, if any,
  are easy to find since the X or Y coordinates are
  already known.
• Vertices which are kept after clipping against
  one window edge are saved for clipping against
  the remaining edges.
• Note that the number of vertices usually changes
  and will often increases.

9
Clipping A Polygon Step by Step
10
Sutherland-Hodgeman Algorithm
Note the difference between this strategy and
the Cohen-Sutherland algorithm for clipping a
line the polygon clipper clips against each
window edge in succession, whereas the line
clipper is a recursive algorithm. Given a
polygon with n vertices, v1, v2,, vn, the
algorithm clips the polygon against a single,
infinite clip edge and outputs another series of
vertices defining the clipped polygon. In the
next pass, the partially clipped polygon is then
clipped against the second clip edge, and so on.
Lets considering the polygon edge from vertex vi
to vertex vi1. Assume that start point vi has
been dealt with in the previous iteration, four
cases will appear.
11
Sutherland-Hodgeman Algorithm(cont.)
12
An Example for the Polygon Clipping
v5
v4
v1
v2
v3
13
Solution
As we said, the Sutherland-Hodgeman algorithm
clip the polygon against one at a time. We start
with the right edge of the clip rectangle. In
order to clip the polygon against the line, each
edge of the polygon have to be considered.
Starting with the edge, represented by a pair of
vertices, v5v1
v5
v5
v4
v1
v1
v1
v2
v3
Clipping edge
Clipping edge
Clipping edge
14
Solution (cont.)
Now v1v2
v5
v4
v1
v1
v1
v2
v2
v3
v2
Clipping edge
Clipping edge
Clipping edge
15
Solution (cont.)
Now v2v3
v5
v4
v1
v1
v2
v2
v3
v2
v3
v2
v3
Clipping edge
Clipping edge
Clipping edge
16
Solution (cont.)
Now v3v4
v5
v4
v4
v1
v1
i1
v2
v2
v3
v3
v2
v3
Clipping edge
Clipping edge
Clipping edge
17
Solution (cont.)
Now v4v5
v5
v5
v5
v4
i2
v4
v1
v1
i1
v2
v2
v3
v2
v3
Clipping edge
Clipping edge
Clipping edge
After these, we have to clip the polygon against
the other three edges of the window in a similar
way.