Carnot Cycle

1
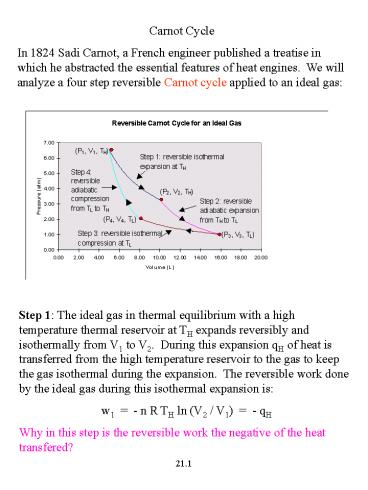
Carnot Cycle In 1824 Sadi Carnot, a French
engineer published a treatise in which he
abstracted the essential features of heat
engines. We will analyze a four step reversible
Carnot cycle applied to an ideal gas
Step 1 The ideal gas in thermal equilibrium with
a high temperature thermal reservoir at TH
expands reversibly and isothermally from V1 to
V2. During this expansion qH of heat is
transferred from the high temperature reservoir
to the gas to keep the gas isothermal during the
expansion. The reversible work done by the ideal
gas during this isothermal expansion is w1 -
n R TH ln (V2 / V1) - qH Why in this step
is the reversible work the negative of the heat
transfered?
2
Sadi Carnot was born in 1796 the son of Lazare
Carnot, a noted French mathematician, engineer,
and general. He began his university studies at
age 16 at the Ecole Polytechnique in Paris. After
two years Sadi left the Ecole to work in the
Corps of Engineers. Unchallenged in the Corps of
Engineers he spent some time analyzing heat
engines, about which little was known of their
theory of operation. In
1824 he published his only work Reflexions sur la
puissance motrice du feu (Reflections on the
Motive Power of Fire), which was mostly ingnored
by his contemporaries. This analysis set upper
limits on the efficiency of steam engines and
paved the way for the development of the 2nd Law
of Thermodynamics. He died in 1832 at the age of
46, the victim of a cholera epidemic. The
figure is taken from a ChemTeam WEB page
maintained by John L. Park at dbhs.wvusd.k12.ca.us
/Gallery/GalleryMenu.html
3
Step 2 The ideal gas expands reversibly and
adiabatically from TH to TL. The reversible work
done by the ideal gas during this adiabatic
expansion is w2 n CV (TL - TH) Could you
derive this expression for the work done in the
adiabatic step? Step 3 The ideal gas in thermal
equilibrium with a low temperature thermal
reservoir at TL is compressed reversibly and
isothermally from V3 to V4. During this
expansion qL of heat is transferred from the
ideal gas to the low temperature reservoir to
keep the gas isothermal during the compression.
The reversible work done by the ideal gas during
the isothermal expansion is w3 - n R TL ln
(V4 / V3) - qL Step 4 The ideal gas is
reversibly and adiabatically compressed back to
its initial state to complete the cycle. The
reversible work done by the ideal gas during this
adiabatic compression is w4 n CV (TH -
TL) The net work done in one complete cycle is
the sum of the work done in each of the cycle
steps wnet w1 w2 w3 w4
- n R TH ln (V2 / V1) n CV (TL - TH)
- n R TL ln (V4 / V3) n CV (TH - TL) The
work done in the adiabatic steps cancels to
give wnet - n R TH ln (V2 / V1) -
n R TL ln (V4 / V3)
4
We can equate relations that we derived earlier
for the adiabatic steps (see the section on
adiabatic processes) CV ln (TH / TL) R ln
(V3 / V2) R ln (V4 / V1) to simplify the
equation for the net work even more wnet - n
R TH ln (V2 / V1) - n R TL ln (V1 / V2)
- n R ln (V2 / V1) (TH - TL) - n R
TH ln (V2 / V1) (TH - TL) / TH
w1 (TH - TL) / TH - qH (TH - TL) /
TH Could you justify the steps in the above
derivation? Remembering the definition of
efficiency of a heat engine we have for the
efficiency of our reversible cyclic Carnot
engine efficiency - wnet / qH (TH - TL)
/ TH Note that the efficiency of the reversible
heat engine does not depend on the nature of the
working fluid, but only depends on the absolute
temperatures between which the engine is
operating. While we used an ideal gas as the
working fluid to derive this result, the result
is general and applies to any reversible heat
engine and in fact represents the maximum
efficiency possible for any engine. Which is more
efficient, your refrigerator or your
freezer? Which has the greater efficiency, an
engine operating between 80 oC and 90 oC or an
engine operating between 90 oC and 100 oC? Could
you sketch how a single reversible Carnot cycle
would appear on a TS diagram, a plot of
temperature versus entropy?
5
A temperature scale is defined by at a minimum
two temperatures and a interpolatable scale
between the values of these two temperatures.
The temperatures that define the scale are known
as fixed points in temperature. They are
associated with highly reproducible systems and
are determined by international agreement. These
fixed points in temperature are chosen by
international agreement. The latest agreement
has been published as The International
Temperature Scale of 1990 (ITS-90) in Metrologia,
273-10 (1990). The efficiency of a heat engine
will be a maximum, if the low temperature
reservoir is at 0 degrees on whatever absolute
temperature scale we choose. The results of the
Carnot cycle therefore define the thermodynamic
scale of temperature in which the lowest fixed
point in temperature is absolute zero. All that
remains to complete the definition of the
thermodynamic temperature scale is to choose one
other fixed point in temperature. If we choose
the other fixed point to be the triple point of
water at which air free ice, liquid water, and
water vapor are all in equilibrium at a
temperature of 273.16 K, then the
thermodynamic and Kelvin scales of temperature
agree with each other.
6
The efficiency of a single reversible Carnot
cycle can also be written as efficiency -
wnet / qH qnet / qH (qH qL) / qH
Equating this expression for efficiency with the
one we developed previously (qH qL) / qH
(TH - TL) / TH gives after rearrangement qH / TH
qL / TL 0
7
By extending this result for the single
reversible Carnot cycle to any general reversible
cyclic process an analytic expression for entropy
can be developed
If we slice the general reversible cycle with a
series of adiabats and isotherms the general
cyclic process can be represented as a sum of
single reversible Carnot cycles S ( qH / TH
qL / TL ) i 0 Why is this sum equal to
zero? The sum is over all of the indvidual
single reversible Carnot cycles that are at least
partly in the general reversible cycle. Notice
that two adjacent single reversible Carnot cycles
will share an edge (see the colored arrows in the
above sketch) and that in the Carnot analysis of
each of these adjacent cycles that edge will be
traversed in opposite directions and the
corresponding terms from the two Carnot cycles
will cancel in the sum. The only terms which
will not cancel are for those edges that are
outside the general cycle (see the edge labeled
with the green arrow).
8
As we let the number of adiabats and isotherms
slicing the general reversible cyclic process
approach infinity
9
Remembering that if the cyclic integral of some
function is equal to zero, then that function is
a state function, we define an analytical
expression for the differential change in the
state function entropy as dS ? dqrev / T