Network Routing Problem

1
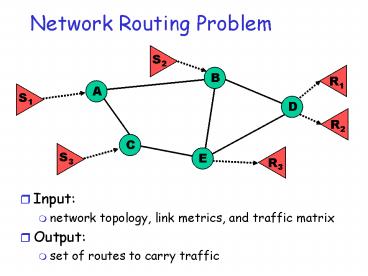
Network Routing Problem
B
A
D
C
E

• Input
• network topology, link metrics, and traffic
  matrix
• Output
• set of routes to carry traffic

2
Network Routing Classical Approach

• Routing as optimization problem
• e.g., minimum total delay in network
• focus on global network performance (social
  optimal)
• performance of individual user not important
• Centralized or distributed algorithms
• e.g., link state or distance vector
• Passive users
• users are oblivious to routing decisions

3
Network Routing Game-Theoretic Approach

• Routing as game between users
• users determine route
• decision based solely on individual performance
  (selfish routing)
• strongly dependent on other users decisions
• Non-cooperative game (non-zero sum)
• users compete for network resources
• Equilibrium point of operation
• Nash equilibrium point (NEP)

4
Selfish Network Routing

• Advantages
• no need of centralized control or global
  agreement on routing algorithm
• individual users performance considered
• greater adaptability
• changes in user demands or changes in network
  conditions
• Disadvantages
• multiple equilibria (eq. selection problem)
• convergence to equilibrium
• no network-wide optimality at equilibrium
• cost of selfish routing
• users must have detailed knowledge of network

5
Applications of Game Theory to Network Routing

• Competitive routing in multiuser communication
  networksA. Orda, R. Rom and N. ShimkinIEEE/ACM
  Transactions on Networking, 1 (5) 1993
• How bad is selfish routing?T. Roughgarden and E.
  TardosJournal of the ACM, 49 (2) 2002
• Selfish routing with atomic playersT.
  RoughgardenACM/SIAM Symp. on Discrete Algorithms
  (SODA) 2005

6
Simple Model Network of Parallel Links
A
B

• set of users share a set of parallel links
• each user has fixed demand (data rate)
• users decide how to split demand across links
• minimize individual cost
• link has a load dependent cost (e.g., delay)

7
Network of Parallel Links

• set of parallel links
• set of users
• each user has a fixed demand (data rate)
• user splits its demand across links
• flow of user i on link l
• flow configuration of user i
• system flow configuration
• feasible configurations
• satisfy nonnegative and demand constraints

8
Users Cost Function

• Cost function of user i
• cost depends on flow configuration of all users
• Assumptions on cost function
• sum of user-link cost function
• can be infinite
• convex in
• when finite, continuously differentiable in
• at least one user with infinite cost can change
  its flow configuration to have finite cost
• aggregate demand must be less than aggregate link
  capacity

9
The Game

• Users individually decide their flow
  configuration
• goal is to minimize its own cost
• Nash Equilibrium Point (NEP)
• system flow configuration such that no user can
  reduce their cost by changing its flow allocation
• is a NEP if for all
  i, the followingholds

10
The Issues

• Existence of NEP
• is at least one NEP guaranteed to always exist
• Uniqueness of NEP
• under which conditions (if any) do we have a
  single NEP
• Convergence to (and stability of) NEP
• play dynamics that lead to a NEP
• System properties at the NEP
• e.g., how does users divide allocate their flows

11
Existence of NEP

• N-person convex game Rosen65
• joint strategy set is convex, closed and bounded
• each players payoff function is convex in their
  own strategy
• existence of NEP proven by Katutani fixed point
  theorem
• Can also show using Kuhn-Tucker conditions
• necessary and sufficient for system flow
  configuration to be a NEP

12
Uniqueness of NEP

• Uniqueness of NEP only under a type of cost
  functions (type-A functions)
• cost function has two parameters users i and
  aggregate of all others
• monotonically increasing in each parameter
• still very general (e.g., M/M/1 delay function)
• Proof by contradiction using Kuhn-Tucker
  conditions

13
System Properties at NEP

• Assume all users share same type-A cost function
• but users can have different demands
• Monotonicity of link usage
• user with higher demand uses more of each and
  every link used
• a user with higher demand uses more links
• Higher capacity links receive more users
• does not hold in general, only under yet another
  type of cost function (which still captures M/M/1)

14
Dynamical System

• Simple case study
• two-users sharing two parallel links
• Dynamical model Elementary Stepwise System
• Users take turns in updating their flow
  configuration
• measure load on links, adjust its flow to
  minimize cost
• flow of user i on link l at step n

15
Convergence to NEP

• Let denote unique NEP of game
• Initialize system with any feasible flow
  configuration f(0)
• Convergence to NEP guaranteed

• Framework used in proof not aplicable in general
• limited to two link, two user structure

16
General Topology
B
A
D
C
E

• Users decide how to split their demands over
  possible paths
• users know network topology (directed graph)

17
Existence and Uniqueness of NEP

• Existence of NEP
• same argument as before (N-person convex game)
• No unique NEP for type-A cost functions
• shown by counterexample
• Uniqueness shown only under very strict
  conditions for cost function
• not very interesting networking scenarios

18
The Price of Anarchy

• Equilibria of non-cooperative games usually
  inefficient
• e.g., prisoners dilemma
• Pareto optimal usually not a NEP
• Quantify inefficiency in terms of a global
  objective
• price of anarchy (coordination versus
  competition)

objective function value at NEP
Price of Anarchy of a Game

optimal objective function value

• if multiple NEP exists, take sup (or inf) over
  NEP set

19
Cost of Selfish Routing

• How does total cost compare?
• flow allocation at a NEP
• optimal flow allocation
• Total cost of flow configuration
• where is load dependent link cost
  function
• e.g., link delay

20
Example (1/4)
r1 0.5
S1
R1
A
B
r2 0.5
S2
R2

• flow configuration cost
• optimal flow allocation
• can be realized with

21
Example (2/4)
r1 0.5
S1
R1
A
B
r2 0.5
S2
R2

• But this is not NEP
• Cost of a flow configuration to user i

• By rerouting traffic user 1 (or 2) can reduce its
  cost

lower cost!
22
Example (3/4)
r1 0.5
S1
R1
A
B
r2 0.5
S2
R2

• NEP given by
• link 1 is a dominant strategy (link 2 never used)
• Cost to user i at NEP
• Total cost of NEP configuration

higher cost!
higher cost
23
Example (4/4)
r1 0.5
S1
R1
A
B
r2 0.5
S2
R2

• Optimal cost
• NEP cost
• Price of Anarchy

• ThmRoughgarden/Tardos00 POA of selfish routing
  w/affine cost functions is at most 4/3
• for any network topology and traffic matrix!

24
Another example (non-linear cost)
r1 0.5
S1
R1
A
B
r2 0.5
S2
R2

• NEP both users only use link 1
• cost is 1
• Optimal 1-e for link 1 and e for link 2
• e depends on d, but is small for large d
• cost 0
• Price of anarchy can be arbitrarily large
• goes to infinity as d goes to infinity

25
So how bad is selfish routing?

• It depends...
• cost functions, network topology, traffic matrix,
  user demands, etc.
• In reality, not so bad
• achieves close to optimal cost in Internet-like
  environments (simulation study)
• Another positive (and nice) result

• ThmRoughgarden/Tardos00 selfish routing is no
  worst than the optimal routing of twice as much
  traffic
• for any cost function, network topology and
  traffic matrix!

26
Title
27
Congestion Control Problem
B
A
D
C
E

• Input
• network topology, routes, link characteristics,
  traffic matrix
• Output
• set of data rates to be used

28
Congestion Control Classical Approach

• Congestion control as optimization problem
• match users demand to network capacity and
  achieve some fairness among users
• focus on global network performance (social
  optimal)
• performance of individual user not important
• Centralized or distributed algorithms
• e.g., TCP, max-min fairness
• Passive users
• users are oblivious to congestion decisions

29
Congestion Control Game-Theoretic Approach

• Congestion control as game between users
• users determine their own data rates
• decision based solely on individual performance
• Non-cooperative game (non-zero sum)
• users compete for network resources
• Equilibrium point of operation
• Nash equilibrium point (NEP)

Key Assumption A higher sending rate do not
necessarily yields better performance for user
30
Routing Games vs Congestion Control Games

• Routing games
• users determine network routes
• multi-path routing and traffic splitting is
  possible
• users data rates are given and must be routed

• Congestion games
• users determine their data rate
• network routes are given (single path)

31
Applications of Game Theory to Congestion Control

• Making greed work in networks a game-theoretic
  analysis of switch service disciplinesS.
  ShenkerIEEE/ACM Transactions on Networking, 3
  (6) 1995
• An evolutionary game-theoretic approach to
  congestion controlD. Menasché, D. Figueiredo, E.
  de Souza e Silva Performance Evaluation, 62 (1-4)
  2005

32
Simple Model Single Bottleneck Link

• set of users share a bottleneck link
• users decide their data rates
• maximize individual performance
• users performance depends on link load
• e.g., quality of service provided by link

33
Single Bottleneck Link

• Users determine sending rate
• Link modeled as M/M/1 queue
• unit capacity
• packet scheduling policy
• Scheduling policy induces average queue length
  for each user
• avg. queue length of user i
• Users utility function
• strictly increasing in
• strictly decreasing in
• convex and derivable everywhere

34
Scheduling Policy

• Determined by system operator
• Allocation function
• scheduling policy P induces an avg. queue length
  for each user given all users data rate
• FIFO example
• Must satisfy some constraints
• aggregate average queue size same as M/M/1
• Allocation function can be realized by different
  service disciplines

35
Fair Share Allocation

• Allocate service capacity fairly among users
  demand
• users requesting less obtain higher priority
• Implemented through a priority queueing algorithm

• Assume r1 lt lt rN

User Priority Level Priority Level Priority Level Priority Level
User A B C D
1 r1 - - -
2 r1 r2 - r1 - -
3 r1 r2 - r1 r3 - r2 -
4 r1 r2 - r1 r3 - r2 r4 - r3
fraction of traffic gets lower priority
36
MAC Set of Monotonic Allocation Functions

• Consider a set of possible allocation functions
• increases, increases
• increases, does not
  decrease
• Includes all typical service disciplines
• FIFO, LIFO, PS, fair share allocation

at ? for all with rk ?
rok
37
The Problem Investigated

• Relationship between NEP and service disciplines
  (MAC functions)
• Which service disciplines yield good NEP?
• Properties of NEP of a given MAC
• efficiency
• fairness
• convergence to equilibrium
• user protection

38
Efficiency of NEP

• Efficiency in terms of Pareto optimal
• no global objective function of system outcome
• Pareto optimal outcome
• no other outcome is preferred by all users

ThmShenker95 There is no allocation function
in MAC such that every NEP is Pareto optimal

• Under some additional constraints fair share is
  always efficient
• constrained users utility function
• symmetric rate vector

39
Uniqueness of NEP

• Allocation functions can induce multiple NEP
• undesirable since users cannot coordinate

• ThmShenker95
• Fair share mechanism always has a unique NEP
• Fair share is the only allocation function that
  always yields a unique NEP

40
Convergence to Equilibrium

• Dynamics through a generalized hill climbing
  algorithm
• users eliminate strategies that always perform
  worst
• system converges to a reduced set of strategies
• Different from best-response dynamics

• ThmShenker95
• With the fair share mechanism, all generalized
  hill climbing algorithm converges to the NEP

• Convergence is also fast (superlinear) and stable

41
Title
42
Application to Multimedia Traffic

• Users share common bottleneck link
• Users choose data rate to be sent by source
• only few data rates available
• Utility given by perceived quality

43
Why Evolutionary Game Theory

• Model how users change their strategy
• Users are not perfect stochastic dynamics,
  myopic, etc
• Which NEP will be achieved (if more than one
  exists)
• Efficiency of selected NEP

Evolutionary Game Theory
44
Entities of Model and Interactions
yields perceived quality to
performance metric feeds
Link model(M/M/1/k or other)
Users(strategy set)
QoS Model(E-model or other)
choice of strategies causes impact on
45
Two-layer Markovian Model
layer 1
users actions
2, 1
3, 0
0, 3
1, 2
link perf.
layer 2
QoS of each user
QoS of each user
QoS of each user
QoS of each user
46
States and Users Utility
number of users selecting strategy l in state
number of data rates available to users
state
utility function of strategy l in state

• No constraints on users utility function
• should be defined for every state

47
Transition Matrix

• Transitions determined by QoS in each state
• rate of change proportional to gain
• transitions can reduce QoS (users make errors)
• Markov chain is ergodic

48
Main Problem Investigated
Assume

• System in steady state
• Users make no mistakes

States that correspond to NEP
States that have non-negligible steady state
probability
What is the relationship?
49
Proposition 1
This state is also a NEP
If a state has non-negligible steady state
probability

• under the condition that this state is contained
  in a quasi-absorbing set

50
Proposition 2
This state also has non-negligible steady state
probability
If a state is a NEP

• proof via simple counter-example

51
Summary of Results

• States with non-negligible SS probability are NEP
• correspond to stable states
• Some NEP are not stable
• system dynamics cannot converge on them
• Still possible to have multiple stable NEP
• not clear where system will converge
• state with highest probability?

52
Title
53
Title