Day 15 WarmUp

1
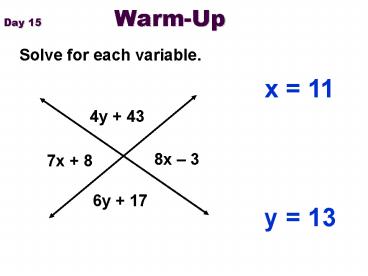
Day 15 Warm-Up
Solve for each variable.
x 11
4y 43
8x 3
7x 8
6y 17
y 13
2
Agenda

• Notes 3.1 3.3
• CW-WS 3.1 3.3
• Homework
• Get the test back??

Wed 1/28 3.2, 3.4
Thur 1/29 Quiz 3.1-3.4 Start 3.5
Fri 1/30 3.6, 3.7
3
3.1 Lines and Angles3.3 Parallel Lines and
Transversals
4
Parallel Planes Planes that do not intersect.
5
Parallel Lines
Parallel Lines Two lines are parallel if and
only if they are in the same plane and do not
intersect.
B
A
D
C
AB ??CD
6
Skew Lines two lines that are NOT in the same
plane and do NOT intersect
7
Example 1
1. A plane parallel to plane AFE.
F
E
Plane BGD
G
D
2. All segments that intersect GB.
A
C
B
3. All segments parallel to FE.
4. All segments skew to ED.
8
Transversal
Transversal A line, line segment, or ray that
intersects two or more lines at different points.
a
A
b
B
Ray AB is a transversal.
9
Special Angles
2
1
4
Interior Angles lie between the two lines (?3,
?4, ?5, and ?6)
3
6
5
8
7
Alternate Interior Angles are on opposite sides
of the transversal. (?3 ?6 AND ?4 and ?5)
Consecutive Interior Angles are on the same
side of the transversal. (?3 ?5 AND ?4 ?6)
10
More Special Angles
Exterior Angles lie outside the two lines (?1,
?2, ?7, and ?8)
2
1
4
3
6
5
8
7
Alternate Exterior Angles are on opposite sides
of the transversal (?1 ?8 and ?2 ?7)
11
Practice Identify each pair of angles as
alternate interior, alternate exterior,
consecutive interior, or vertical.
a. ?1 and ?2
1
Alt. Ext. Angles
6
7
3
b. ?6 and ?7
4
8
Vertical Angles
5
2
c. ?3 and ?4
Alt. Int. Angles
d. ?3 and ?8
Consec. Int. Angles
12
Alternate Interior Angles Theorem
If two parallel lines are cut by a transversal,
then each pair of alternate interior angles are
congruent.
8
1
7
?2 ? ?6
2
6
3
5
4
?3 ? ?7
13
Alternate Exterior Angles Theorem
If two parallel lines are cut by a transversal,
then each pair of alternate exterior angles are
congruent.
8
1
7
?1 ? ?5
2
6
3
5
4
?4 ? ?8
14
Consecutive Interior Angles Theorem
If two parallel lines are cut by a transversal,
then each pair of consecutive interior angles are
supplementary.
m?2 m?3 180
8
1
7
2
6
m?6 m?7 180
3
5
4
15
More Special AnglesCorresponding Angles
Same location at different intersections.
2
bottom right
1
Top left
4
3
6
bottom right
5
Top left
8
7
Drive on the transveral to the intersection.
16
Name two pairs of corresponding angles
2
1
4
3
6
4
8
7
17
If two parallel lines are cut by a transversal,
then each pair of corresponding angles is
congruent
8
1
7
2
6
3
5
4
18
Perpendicular Transversal Theorem
If a transversal is perpendicular to one of the
two parallel lines, then it is perpendicular to
the other.
19
Example 2 In the figure, p??q. If m?5 28,
find the measure of each angle.
28
a. m?8
q
2
1
p
b. m?1
28
4
3
c. m?3
152
6
5
8
7
d. m?4
28
20
Example 3 In the figure, s??t. Find the m?CBG.
t
Step 1 Solve for x.
G
S
B
3x 5 4x - 29
3x - 5
C
-5 x - 29
4x -29
24 x
Step 2 m?CBG m?ABE 3x -5.
3x-5 3(24) 5 72-5 67
21
Whiteboard Practice Identify each pair of
angles as alt. interior, alt. exterior,
consecutive interior, or vertical.
10
11
9
12
16
alternate exterior
8
1
15
13
7
2
6
14
3
5
4
22
Whiteboard Practice Identify each pair of
angles as alt. interior, alt. exterior,
consecutive interior, or vertical.
10
11
9
12
16
consecutive interior
8
1
15
13
7
2
6
14
3
5
4
23
Whiteboard Practice Identify each pair of
angles as alt. interior, alt. exterior,
consecutive interior, or vertical.
10
11
9
12
16
alternate interior
8
1
15
13
7
2
6
14
3
5
4
24
Whiteboard Practice Identify each pair of
angles as alt. interior, alt. exterior,
consecutive interior, or vertical.
10
11
9
12
16
alternate exterior
8
1
15
13
7
2
6
14
3
5
4
25
Whiteboard Practice Identify each pair of
angles as alt. interior, alt. exterior,
consecutive interior, or vertical.
10
11
9
12
16
consecutive interior
8
1
15
13
7
2
6
14
3
5
4
26
Class WorkWS 3.1 Band WS 3.3
27
Homework

• P. 132 (13 problems)
• 10 18 even, 21 26 all, 41 42
• P. 146 (10 problems)
• 8 26 even