Robustness, evolvabilityscalability, verifiability

1
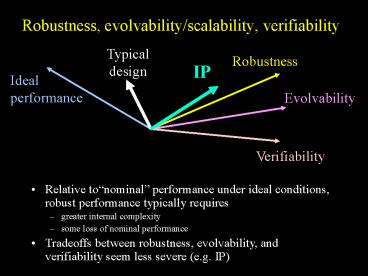
Robustness, evolvability/scalability,
verifiability
Robustness
Ideal performance

• Relative tonominal performance under ideal
  conditions, robust performance typically requires
• greater internal complexity
• some loss of nominal performance
• Tradeoffs between robustness, evolvability, and
  verifiability seem less severe (e.g. IP)

2
Robustness, evolvability/scalability,
verifiability
Ideal performance
Robustness
Evolvability
Verifiability

• There is much anecdotal evidence and some new
  theoretical support as well for the compatibility
  of robustness, evolvability, and verifiability
• That a system is not merely robust, but
  verifiably so, is an important engineering
  requirement and major research challenge
• Verifiability in forward engineering translates
  into comprehensibility in reverse engineering of
  biological systems
• This research direction may be good news for
  understanding complex biological processes

3
Robustness of HOT systems
Fragile
Fragile (to unknown or rare perturbations)
Robust (to known and designed-for uncertainties)
Uncertainties
Robust
4
Sources of uncertainty

• In a system
• Environmental perturbations
• Component variations
• In a model
• Parameter variations
• Unmodeled dynamics
• Assumptions
• Noise

Fragile
Robust
5
Sources of uncertainty
Fragile
?
Robust
6
Typically NP hard.
?
7
Typically coNP hard.

• Fundamental asymmetries
• Between P and NP
• Between NP and coNP

?

• More important problem.
• Short proofs may not exist.

Unless theyre the same
8
Robustness, evolvability, scalability,
verifiability
?
9
?
10
?
11
Verifiability (short proofs) ? Extra robustness
12
How do we prove that

• Standard techniques include relaxations, Grobner
  bases, resultants, numerical homotopy, etc
• Powerful new method based on real algebraic
  geometry and semidefinite programming (Parrilo,
  Shor, )
• Nested series of polynomial time relaxations
  search for polynomial sized certificates
• Exhausts coNP (but no uniform bound)
• Relaxations have both computational and physical
  interpretations
• Beats gold standard algorithms (eg MAX CUT)
  handcrafted for special cases
• Completely changes the P/NP/coNP picture

13
Robustness and verification
Complexity considerations are critical. Need
procedures that avoid exponential growth, and run
in reasonable time. For this, need to
understand computational complexity classes, and
how to deal with them. Where do our typical
problems live (P,NP,co-NP)? How to systematically
obtain tractable relaxations.
14
Asymmetry between NP vs. co-NP

• Given a propositional formula (e.g. 3SAT)
• Have to convince you that it is satisfiable (NP)
• Simple. Just produce a valid assignment.
• But how do I convince you that it is not? (co-NP)
• In the general case, may have to try all the
  solutions

Complementary problems, but very different.
15
Traveling Salesman
Nonnegativity
Co-NPC
NPC
P
co-NP (concise counterexamples)
NP (concise proofs)
Linear programming
16
NP vs. co-NP Optimization
Upper bounds are in co-NP. Proofs needed.
Lower bounds are in NP. Given by feasible points.
17

• NP vs. co-NP Robustness
• Find bad events

• or
• Safety guarantees

Bad events are easy to describe (NP) Safety
proofs could potentially be long (co-NP)
18
How to do this computationally? On the NP side,
search for solutions. co-NP side, look for
simple proofs relaxations. For a very broad
class of problems, can efficiently search over
proofs of bounded complexity.
19
More powerful bounds for the co-NP side
Semialgebraic geometry convex optimization
(SDP)

• Polynomial time computation.
• Never worse than the standard.
• Exhausts co-NP.

20
A key insight
Think of LMIs as quadratic forms, not as
matrices. LMIs quadratic forms, that are
positive definite.

• General forms , not necessarily quadratic.

• Instead of nonnegativity (NP-hard), use sum of
  squares.

SOS multivariable forms, that are sum of
squares.
21
Sums of squares (SOS)
A sufficient condition for nonnegativity

• Convex condition (Shor, 1987)
• Efficiently checked using SDP (Parrilo). Write

where z is a vector of monomials. Expanding and
equating sides, obtain linear constraints among
the Qij. Finding a PSD Q subject to these
conditions is exactly a semidefinite program
(LMI).
22
Nested families of SOS (Parrilo)
exhaust co-NP
23
?0
24
A Few Applications

• Nonlinear dynamical systems
• Lyapunov function computation
• Bendixson-Dulac criterion
• Robust bifurcation analysis
• Continuous and combinatorial optimization
• Polynomial global optimization
• Graph problems e.G. Max cut
• Problems with mixed continuous/discrete vars.
• Hybrid???

Lets see some examples
25
Continuous Global Optimization

• Polynomial functions NP-hard problem.
• A simple relaxation (Shor) find the maximum
  ?such that f(x) ? is a sum of squares.
• Lower bound on the global optimum.
• Solvable using SDP, in polynomial time.
• A concise proof of nonnegativity.
• Surprisingly effective (Parrilo Sturmfels 2001).

26

• Much faster than exact algebraic methods (QE,GB,
  etc.).
• Provides a certified lower bound.
• If exact, can recover an optimal feasible point.
• Surprisingly effective
• In more than 10000 random problems, always the
  correct solution
• Bad examples do exist (otherwise NPco-NP), but
  rare.
• Variations of the Motzkin polynomial.
• Reductions of hard problems.
• None could be found using random search

27
Finding Lyapunov functions

• Ubiquitous, fundamental problem
• Algorithmic LMI solution

Convex, but still NP hard.
Test using SOS and SDP.
After optimization coefficients of V.
A Lyapunov function V, that proves stability.
28
Finding Lyapunov functions

• Ubiquitous, fundamental problem
• Algorithmic LMI solution

Given
Propose
After optimization coefficients of V.
A Lyapunov function V, that proves stability.
29
Conclusion a certificate of global stability
30
DS applications Bendixson-Dulac

• In 2D rules out periodic orbits.
• Higher dimensional generalizations (Rantzer)
  provide
• Weaker stability criterion than Lyapunov
  (allowing a zero-measure set of divergent
  trajectories).
• Convexity for synthesis.
• How to search for ? ?

31
DS applications Bendixson-Dulac

• Restrict to polynomial (or rational) solutions,
  use SOS.
• As for Lyapunov, now a fully algorithmic
  procedure.

Given
Propose
After optimization
32
Conclusion a certificate of the inexistence of
periodic orbits
x ' y


2
2
y ' - x - y x
y


3
2
1
0
y
-1
-2
-3
-3
-2
-1
0
1
2
3
x
33
Conclusion a certificate of the inexistence of
periodic orbits
x ' y


saddle
y
stable
34
More general framework

• A model co-NP problem
• Check emptiness of semialgebraic sets.
• Obtain LMI sufficient conditions.
• Can be made arbitrarily tight, with more
  computation.
• Polynomial time checkable certificates.

35
Semialgebraic Sets

• Semialgebraic finite number of polynomial
  equalities and inequalities.
• Continuous, discrete, or mixture of variables.
• Is a given semialgebraic set empty?
• Feasibility of polynomial equations NP-hard
• Search for bounded-complexity emptiness proofs,
  using SDP. (Parrilo 2000)

36
Positivstellensatz (Real Nullstellensatz)
if and only if

• Stengle, 1974
• Generalizes Hilberts Nullstellensatz and LP
  duality
• Infeasibility certificates of polynomial
  equations over the real field.
• Parrilo Bounded degree solutions computed via
  SDP!
• ? Nested family of polytime relaxations for
  quadratics, the first level is the S-procedure

37
Combinatorial optimization MAX CUT

• Given a graph
• Partition the nodes in two subsets

• To maximize the number of edges between the two
  subsets.

A mathematical formulation
Hard combinatorial problem (NP-complete).
Compute upper bounds using convex relaxations.
38
Standard semidefinite relaxation
Dual problems
This is just a first step. We can do better! The
new tools provide higher order relaxations.

• Tighter bounds are obtained.
• Never worse than the standard relaxation.
• In some cases (n-cycle, Petersen graph),
  provably better.
• Still polynomial time.

39
MAX CUT on the Petersen graph
The standard SDP upper bound 12.5 Second
relaxation bound 12. The improved bound is
exact. A corresponding coloring.
40
Stronger µ upper bounds

• Structured singular value µ is NP-hard (as
  general QP)
• Standard µ upper bound can be interpreted
• As a computational scheme.
• As an intrinsic robustness analysis question
  (time-varying uncertainty).
• As the first step in a hierarchy of convex
  relaxations.
• For the four-block Morton Doyle counterexample
• Standard upper bound 1
• Second relaxation 0.895
• Exact µ value 0.8723

41
What is the message ?
What happens in the broader setting of
robustness and verification?
42
Line of Attack

• Want to decouple
• System complexity
• Complexity of verification.

• Even for extremely complex systems, there may
  exist simple robustness proofs. Try to look for
  those first

43
What is the message ?
WHY ?
44

• Partly intrinsic (as in optimization problems),
  but can also be a consequence of design.

• Robustness, verifiability, and complexity are
  inextricably linked.
• Lots of circumstantial evidence
• All our previous experience in robustness
  analysis and optimization µ upper bounds, etc.
• Hard mathematical results, linking complexity
  with distance to set of ill-posed instances
  (Smale, etc).

45
What are these short proofs?

• Admit multiple interpretations
• Alternative reformulations (perhaps more
  natural).
• Relaxation of assumptions (LTI -gt LTV,
  commutativity, etc.)
• Purely computational schemes.
• Bounded depth derivations.

46
About synthesis

• Everything discussed is for analysis or
  verification.
• Synthesis is a much more complicated beast.

• In general, in higher complexity classes, harder
  than NP-hard (Tierno Doyle 1995).
• Alternating quantifiers, relativized Turing
  machines the polynomial time hierarchy.

47
The polynomial time hierarchy
Synthesis
NP
Co-NP
Analysis
P
48
Why are LMIs ubiquitous?

• In general is ?2-hard.
• No current hope of solving this efficiently.
• But when P(x,y) is quadratic in x and affine in
  y
• Drops two levels to P, polynomial time !

49
P(x,y) is quadratic in x and affine in y
50

• Synthesis results depend on hand-crafted
  tricks that we dont fully understand yet.
• Until recently we could say the same about
  analysis, where custom techniques abound.
• For analysis, theres a method in the madness,
  earlier results unified and expanded.

51
Summary

• Unified framework for continuous and discrete
  problems.
• A common language polynomial equations and
  inequalities.
• Extremely powerful and general. (Nonlinear,
  hybrid,)
• eg. nonlinearity scales computation but not
  fundamentally different.
• Very different problems. Same solution
  techniques.
• The basic tool sum of squares decomposition.
• Hierarchies of relaxations, arbitrarily tight.
• Tradeoff between computation and accuracy.
• Generalizes many known techniques.

52
Network protocols.
Files
HTTP
TCP
IP
packets
packets
packets
packets
packets
packets
Routers
53
Mice
Network
Sources
Elephants
54
Router queues
Mice
Delay sensitive
Network
Sources
Bandwidth sensitive
Elephants
55
Log(bandwidth)
achievable
not
Rate distortion theory studies tradeoffs between
bandwidth and distortion from lossy coding.
Distortion
56
Log(bandwidth)
cheap
Expensive
Log(delay)

• Well focus to begin with on similar tradeoffs
  in internetworking between bandwidth and delay.
• Well assume TCP (via retransmission) eliminates
  loss, and will return to this issue later.

57
Log(bandwidth)
BW
Bulk transfers (most packets)
Web navigation, voice (most files)
Delay

• Mice many small files of few packets which the
  user presumably wants ASAP
• Elephants few large files of many packets for
  which average bandwidth will be more important
  than individual packet delay
• Most files are mice but most packets are in
  elephants
• which is the manifestation of fat tails in the
  web and internet.

Log(delay)
58
Log(bandwidth)
BW
Bulk transfers (most packets)
Web navigation, voice (most files)
Delay
Claim I Current traffic dominated by these two
types of flows
Log(delay)
Claim II Intrinsic feature of many future
network applications
59
Log(bandwidth)
BW
Bulk transfers (most packets)
Web navigation, voice (most files)
Claim (channel) We can tweak TCP using ECN and
REM to make these flows co-exist.
Delay

• Specifically
• Keep queues empty (ECN/REM).
• BW slightly improved (packet loss)
• Delay greatly improved (queuing)
• Provision network for BW
• Free QOS for Delay
• Network level stays simple

Log(delay)
Currently Delays are aggravated by queuing delay
and packet drops from congestion caused by BW
traffic?
60
Log(bandwidth)
BW
The rare traffic that cant or wont will be
expensive, and essentially pay for the rest.
Delay
Expensive
Log(delay)
Claim (source) Many (future) applications are
natural and intrinsically coded into exactly this
kind of fat-tailed traffic.
61
Fat tailed traffic is intrinsic

• Two types of application traffic are important
  communications and control
• Communication to and/or from humans (from web to
  virtual reality)
• Sensing and/or control of dynamical systems
• Claim both can be naturally coded into
  fat-tailed BW delay traffic
• This claim needs more research

62
BW
Log(bandwidth)
Abstraction
Expensive
Delay
Log(delay)

• Separate source and channel coding
• Source is coded into
• Delay sensitive mice
• Bandwidth sensitive elephants
• Channel coding congestion control

63
Scalable Congestion Control
(Paganini, Doyle Low 01)
ROUTING DELAY
x source rates
y aggregate link flows
LINKS
SOURCES
p link prices
q aggregate prices per source
64
Robustness, evolvability/scalability,
verifiability
Robustness
Ideal performance
65
Network protocols.
Files
HTTP
TCP
IP
packets
packets
packets
packets
packets
packets
Routers
66
The Internet hourglass
IP
From Hari Balakrishnan
67
The Internet hourglass
Everything on IP
IP
From Hari Balakrishnan
68
Applications
Robust Mesoscale
TCP/ IP
Robust, yet fragile
Hardware
69
Uncertainty
Robust Mesoscale
Robust
Uncertainty
70
Yet fragile
Difficult to change
Robust Mesoscale
71
Yet fragile
Protocols allow for the creation of large complex
networks, with rare but catastrophic cascading
failures.
72
Various functionality
Digital
Analog substrate
73
Applications
Software Hardware
Modern Computing
Operating System
Hardware
74
Robust, yet fragile
75
Consumers
Barter
Commodities
76
(No Transcript)
77
The hourglass
Garments
Dress
Shirt
Slacks
Lingerie
Coat
Scarf
Tie
Wool
Cotton
Nylon
Rayon
Polyester
Material technologies
78
Energy

• 110 V, 60 Hz AC
• Gasoline
• ATP, glucose, etc
• Proton motive force

79
Applications

• Decentralized
• Asynchronous
• Robust to
• Network topology
• Application traffic
• Delays, link speeds

TCP/ IP
Hardware
High performance
Necessity Essentially only one design is possible
80
The existing design is incredible, but
Applications

• Decentralized
• Asynchronous
• Robust to
• Network topology
• Application traffic
• Delays, link speeds

TCP/ IP
Hardware
Its a product of evolution, and is not optimal.
High performance
Necessity Essentially only one design is possible
81
Control Theory
Information Theory
Computational
Theory of Complex systems?
Complexity
Statistical Physics
Dynamical Systems
1 dimension ?
82
Control Theory
Information Theory
Biology
Computational

• Non-equilibrium
• Highly tuned or optimized
• Finite but large dimension

Complexity
Statistical Physics
Dynamical Systems
1 dimension ?
83
Control Theory
Information Theory
Theory needs
Computational

• Integrated horizontally and vertically
• Horizontal control, communications, computing
• Vertical multiscale physics
• Status nascent but promise results
• Bonus unexpected synergy

Complexity
Statistical Physics
Dynamical Systems
1 dimension ?
84
Control Theory
Information Theory
Computational

• Ubiquity of power laws
• High shear turbulence
• Dissipation
• Quantum/classical transition
• Quantum measurement

Complexity
Statistical Physics
Dynamical Systems
1 dimension ?