Tutorial for solution of Assignment week 39 - PowerPoint PPT Presentation
1 / 46
Title:
Tutorial for solution of Assignment week 39
Description:
'Construct a time series graph of the fluctuations of the dollar exchange rate, ... 'Construct also a point plot for all pairs (yt-1 , yt) and try to visually ... – PowerPoint PPT presentation
Number of Views:155
Avg rating:3.0/5.0
Title: Tutorial for solution of Assignment week 39
1
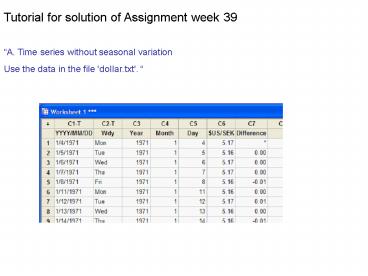
Tutorial for solution of Assignment week 39 A.
Time series without seasonal variation Use the
data in the file 'dollar.txt'.
2
Construct a time series graph of the
fluctuations of the dollar exchange rate, yt, for
the period 1994-1998.
3
(No Transcript)
4
Note! The time scale is best set to index here as
the days are not consecutive in time series
(Saturdays, Sundays and other holidays are not
present)
5
Construct also a point plot for all pairs (yt-1
, yt) and try to visually estimate how strong the
correlation between two consecutive observations
is (autocorrelation).
6
(No Transcript)
7
Strong positive autocorrelation!
How do the estimated autocorrelations change
with increasing timelags between
observations? To estimate the autocorrelation
function, copy the relevant rows (data for
1994-1998) of column US/SEK to a new column and
use the autocorrelation function estimation on
that column
8
(No Transcript)
9
(No Transcript)
10
As was deduced from the scatter plot, the
autocorrelations are strongly positive. The
autocorrelations do not change very much with
increasing time lags. Note that this is what we
see when the time series is non-stationary (has a
trend).
11
Construct a time series graph of the changes zt
yt - yt-1 of the dollar exchange rate. Then try
to judge upon how the estimated autocorrelations
for the series zt change with the time lag
between observations and check your judgement by
estimating the autocorrelations. The changes
are already present in the column Difference.
The analogous procedures are applied to this
column to produce the time series graph and the
estimated acf plot, i.e. by including only values
where column Year is ? 1994.
12
Noisy plot ? As previously plot zt vs. zt 1
Seems to be no autocorrelation at all
13
Our conclusions are verified!
14
B. Time series with seasonal variation Use the
time series of monthly discharge in the lake
Hjälmaren (Hjalmarenmonth.txt), which you have
used in the assignment for week 36. Compute the
autocorrelation function (Minitab Stat?Time
series?Autocorrelation) for the variable
Discharge.m.
15
Deseasonalise the time series and make a new
graph of the seasonally adjusted values. Try to
visually estimate how the autocorrelations look
like and check your judgement by computing the
autocorrelation function.
Additive model for deseasonalization seems best!
16
(No Transcript)
17
Indicates positive autocorrelation
Plot DESE1(t) vs. DESE1(t-1)
18
Indication confirmed!
19
C. Forecasting with autoregressive models Data
set The Dollar Exchange rates Consider again
the time series of dollar exchange rates for the
period 1994-1998. Then use the Minitab time
series module ARIMA (see further below) to
estimate the parameters in an AR(1)-model (1
nonseasonal autoregressive parameter) and plot
the observed values together with forecasts for a
period of 20 days after the last observed
time-point.
Use the already created column of US/SEK
exchange rates from 1994-1998 (there is no
opportunity in Minitabs ARIMA module to just
analyze a subset of a column like in the graphing
modules)
20
Forecasts for a 20 days period are requested.
(Origin field is left blank analogously to
previous modules)
See next slide!
Three new columns should be entered here!
21
Must be checked (not default)
Should always by checked for diagnostic purposes
22
Final Estimates of Parameters Type Coef
SE Coef T P AR 1 0.9971
0.0026 385.44 0.000 Constant 0.021782
0.001280 17.02 0.000 Mean 7.4405
0.4371 Number of observations 1229 Residuals
SS 2.45718 (backforecasts excluded)
MS 0.00200 DF 1227 Modified
Box-Pierce (Ljung-Box) Chi-Square statistic Lag
12 24 36 48 Chi-Square
9.0 22.9 33.3 38.2 DF 10 22
34 46 P-Value 0.529 0.410 0.504
0.786
Significant!
Keep in mind for comparison with next model
OK!
23
Forecasts from period 1229
95 Percent Limits Period
Forecast Lower Upper Actual 1230
7.79895 7.71122 7.88668 1231 7.79790
7.67401 7.92178 1232 7.79685 7.64535
7.94836 1233 7.79581 7.62112 7.97050 1234
7.79477 7.59974 7.98979 1235 7.79373
7.58040 8.00706 1236 7.79270 7.56261
8.02278 1237 7.79167 7.54605 8.03728 1238
7.79064 7.53051 8.05077 1239 7.78961
7.51581 8.06342 1240 7.78859 7.50184
8.07534 1241 7.78757 7.48850 8.08664 1242
7.78655 7.47572 8.09739 1243 7.78554
7.46344 8.10764 1244 7.78453 7.45161
8.11745 1245 7.78352 7.44018 8.12687 1246
7.78252 7.42912 8.13592 1247 7.78152
7.41839 8.14464 1248 7.78052 7.40798
8.15306 1249 7.77952 7.39786 8.16119
These forecasts and prediction limits are stored
in columns C12, C13 and C14 (as entered in dialog
box)
24
Seems to be OK (as was confirmed by the Ljung-Box
statistic)
25
Use the stored prediction limits to calculate the
widths of the prediction intervals
The column widths_1 (C15) will later be compared
with the widths from another model
26
Investigate also if the forecasts can improve by
instead using an AR(2)-model.
Dont forget to enter new columns here!
27
Final Estimates of Parameters Type Coef
SE Coef T P AR 1 1.0107
0.0286 35.35 0.000 AR 2 -0.0138 0.0285
-0.48 0.629 Constant 0.023161 0.001280 18.09
0.000 Mean 7.4372 0.4110 Number of
observations 1229 Residuals SS 2.45873
(backforecasts excluded) MS
0.00201 DF 1226 Modified Box-Pierce
(Ljung-Box) Chi-Square statistic Lag
12 24 36 48 Chi-Square 10.2 24.0
34.3 39.3 DF 9 21 33
45 P-Value 0.337 0.292 0.403 0.710
Non-significant!
Slightly larger than in AR(1)-model
Still OK!
28
(No Transcript)
29
Calculate widths for the new prediction intervals
30
Make a time series plot of the intervals widths
from the two analyses.
31
Slightly wider prediction intervals with
AR(2)-model (widths_2) ? Forecasts do not improve
with AR(2)-model
32
Finally perform a residual analysis of the
errors in the one-step-ahead forecasts (can be
asked for under the Graph button in the dialog
box. By residuals we mean here the errors in the
one-step-ahead forecasts). Are there any signs of
serial correlations in the residuals?
AR(1)
AR(2)
No signs of serial correlations in resiaduals in
any of the models
33
D. ARIMA models and differentiation In this task
you will first have to judge upon whether you
need to differentiate the current time series (
zt yt - yt-1 ) before forecasting with an
ARMA-model can be applied. Then you shall try
different models with a number of parameters to
find the model that gives the least
one-step-ahead prediction errors on the average.
Finally you shall make some residual plots to
investigate if the selected model of forecasting
can be improved. Forecasting monthly dollar
exchange rates in Danish crowns (DKK) Data set
The Dollar-Danish Crowns Exchange rates
34
D.1. The need for differentiation Construct a
time series graph for the monthly means of dollar
exchange rates in Danish crowns (file DKK.txt).
Then estimate the autocorrelations and display
them in a graph. Does the time series show any
obvious upward or downward trend?
35
Note that the y-axis do not start at zero!
A slight upward trend may be concluded Are there
any signs of long-time oscillations in the time
series (that can be seen from the time series
graph)? Yes, there seem to be a cyclical
variation with cycle periods longer than a year.
36
Is there a fast cancel-out in the
autocorrelations? No, the cancel-out is not
fast (although the spikes come quickly within the
red limits) Is there need for differentiation to
get a time series suitable for ARMA-modelling? Pr
obably, but not certainly!
37
D.2 Fitting different ARMA-models Calculate the
estimated autocorrelations possibly after
differentiation of the original series and
display these estimates in a graph.
Without differentiation
(Slowly) decreasing postive autocorrelations. One
positive spike (at lag 1) in SPAC ? Either this
is a non-stationary time series or an AR(1)-time
series with a ? close to 1.
38
With first-order differentiation (use the ready
series of differences)
No obvious pattern in any of these two plots. ?
The differentiated series may be an ARMA-series
39
Then try to predict the dollar exchange rate by
combining differentiation with ARMA-models of
different orders. Strategy On original
series, try AR(1) On differentiated series, try
AR(1), AR(2), MA(1), MA(2), ARMA(1,1),
ARMA(1,2), ARMA(2,1) and ARMA(2,2) Compare the
values of MS from each model. This measure
corresponds with one-step-ahead prediction errors
on the average.
40
None of the models on the differentiated series
produces better MS value than the AR(1) on
original series, but MS seems to decrease with
larger complexity.
41
What happens if one tries to fit a very complex
model with a lot of parameters to the
observations? Study e.g. ARMA(3,3) and
ARMA(4,4) on the differentiated series
42
Final Estimates of Parameters Type Coef
SE Coef T P AR 1 -0.1113
0.3369 -0.33 0.742 AR 2 0.4786 0.2274
2.10 0.038 AR 3 0.3689 0.3237 1.14
0.258 MA 1 -0.1098 0.2941 -0.37
0.710 MA 2 0.4351 0.2136 2.04
0.045 MA 3 0.6165 0.2846 2.17
0.033 Constant 0.000924 0.001931 0.48
0.634 Differencing 1 regular difference Number
of observations Original series 95, after
differencing 94 Residuals SS 3.25649
(backforecasts excluded) MS
0.03743 DF 87 Modified Box-Pierce (Ljung-Box)
Chi-Square statistic Lag 12 24
36 48 Chi-Square 4.9 17.3 26.4
39.5 DF 5 17 29
41 P-Value 0.425 0.431 0.606 0.537
ARMA(3,3)
Even lower than in ARMA(2,2)
No severe problems but not all parameters are
significant!
43
No severe problems here either, but spikes seem
to increase with lag!
44
Unable to reduce sum of squares any
further Final Estimates of Parameters Type
Coef SE Coef T P AR 1
0.4196 2.3514 0.18 0.859 AR 2 0.4329
0.4304 1.01 0.317 AR 3 0.0536
1.2079 0.04 0.965 AR 4 -0.0652 0.7425
-0.09 0.930 MA 1 0.4119 2.3452 0.18
0.861 MA 2 0.3871 0.4030 0.96
0.340 MA 3 0.3397 1.0707 0.32
0.752 MA 4 -0.1736 1.2715 -0.14
0.892 Constant 0.000597 0.001779 0.34
0.738 Differencing 1 regular difference Number
of observations Original series 95, after
differencing 94 Residuals SS 3.26434
(backforecasts excluded) MS
0.03840 DF 85
Estimation problems!
ARMA(4,4)
None of the parameters are significant! Estimation
problems and an increase in MS.
Increased!
45
The conclusion must be that an AR(1)-model on
original data seems to be the best. D.3.
Residual analysis Construct a graph for the
residuals (the one-step-ahead prediction errors)
and examine visually if anything points to a
possible improvement of the model.
SAC and SPAC of residuals do not indicate that
another ARIMA-model should be used.
46
There do not seem to be any violations of the
assumption of normal distribution and constant
variance either.