Transition State Theory - PowerPoint PPT Presentation
1 / 6
Title:
Transition State Theory
Description:
can be solved for the concentration of the activated complex and used to ... collision theory (see the problem at the end of the Notes of Collision Theory) ... – PowerPoint PPT presentation
Number of Views:2558
Avg rating:3.0/5.0
Title: Transition State Theory
1
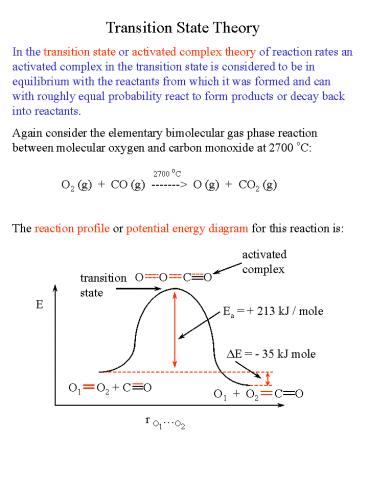
Transition State Theory In the transition state
or activated complex theory of reaction rates an
activated complex in the transition state is
considered to be in equilibrium with the
reactants from which it was formed and can with
roughly equal probability react to form products
or decay back into reactants. Again consider the
elementary bimolecular gas phase reaction between
molecular oxygen and carbon monoxide at 2700
oC 2700 oC O2 (g) CO (g)
-------gt O (g) CO2 (g) The reaction
profile or potential energy diagram for this
reaction is
activated complex
transition state
E
Ea 213 kJ / mole
DE - 35 kJ mole
O1 O2 C O
r O1O2
2
The kinetics that pass through the transition
state can be described by the reaction sequence
k
O2 (g) CO (g) ltgt
-----gt O (g) CO2 (g)
The rate of the reaction can be written in terms
of the rate at which the activated complex reacts
to form products - d CO / dt k
OOCO Since the activated complex is presumed
to be in equilibrium with the reactants O2 (g)
CO (g) ltgt OOCO (g) the equilibrium
constant expression for this equilibrium Kc
OOCO / ( O2 CO ) can be solved for the
concentration of the activated complex and used
to eliminate it from the rate equation - d CO
/ dt k Kc O2 CO The rate at which the
activated complex decays into products will be
proportional to the frequency of the critical
asymmetric vibration, n, in the activated
complex, which would lead to the desired products
The rate constant for decay of the activated
complex can thus be written k k n k
is the tranmission coefficient and accounts for
the fact that the activated complex has some
probability of decaying back to reactants. What
can you say about the possible values for k?
3
Setting the critical vibrational energy equal to
the available thermal energy h n kB T gives
on substitution of these results into the rate
equation - d CO / dt k ( kB T / h ) Kc
O2 CO The equilibrium constant based on
concentrations can be related to the
thermodynamic equilibrium constant Kc
OOCO / ( O2 CO ) R T POOCO / (
PO2 PCO ) ( R T / Po ) (POOCO / Po) / ((
PO2 / Po) (PCO / Po)) ( R T / Po ) K
What assumption was made in this last
derivation? The thermodynamic equilibrium
constant can be related to the standard Gibbs
free energy of activation K e - (DGo) / R
T which in turn can be related to the standard
enthalpy and entropy of activation K e -
(DGo) / R T e - (DHo) / R T e (DSo) / R
Substituting these results into the rate
equation - d CO/dt k (kB T / h) (R T / Po)
e (DSo) / R e- (DHo) / R T O2 CO allows
the rate constant to be identified as
k k ( kB T / h ) ( R T / Po ) e (DSo) / R
e - (DHo) / R T k R2 T2 / ( No Po h ) e
(DSo) / R e - (DHo) / R T
4
Using the more general definition relating the
rate constant and the activation energy that we
introduced earlier (see notes of the Temperature
Dependence of Reaction Rates) Ea R T2 d (ln
k) / dT R T2 d/dT ln k R2 T2 / ( No
Po h ) e (DSo) / R e - (DHo) / R T
R T2 d/dT ln (k R2 e (DSo) / R / (No Po h
)) ln (T2) - (DHo) / (R T)
R T2 2 / T (DHo) / ( R T2 ) 2 R
T (DHo) Solving this expression for the
enthalpy of activation and substituting into the
expression for the rate constant gives k k (
R2 T2 / ( No Po h ) e (DSo) / R e2 e - Ea /
R T Comparing this result with the Arrhenius
equation allows the frequency or pre-exponential
factor to be identified as A k ( R2 T2 / (
No Po h ) e (DSo) / R e2
5
For the formation of the activated complex O2
(g) CO (g) ltgt OOCO (g) a reasonable
estimate of the entropy of activation is (DSo)
- 133 J / mole K Why is the entropy of
activation negative? Assuming a transmission
coefficient of k 1, the frequency factor is
(8.314 J / mole K)(0.08314 dm3 bar /
mole K) (2700 K)2 A 1 --------------------
--------------------------------------------------
- (6.022?1023 mole-1)(1 bar) (6.626 ?
10-34 J sec) x e ( -133 kJ / mole K / 8.314
kJ / mole K ) e2 1.0 1010 dm3 / mole
sec This frequency factor is in better agreement
with the experimental frequency factor (Aexp 3.5
109 dm3 mole-1 sec-1) than was the frequency
factor calculated using collision theory (see the
problem at the end of the Notes of Collision
Theory).
6
Derive an equation for the frequency factor for
the isomerization of cyclopropane to propene at
750 K Note the equations that will apply in
this unimolecular reaction will be slightly
different than those derived in the notes for a
bimolecular reaction. To obtain the appropriate
equations you will have to reproduce the
derivation for the unimolecular case (the
derivations are quite similar). Using the
experimental frequency factor taken from the
literature Kinetic Data on Gas Phase
Unimolecular Reactions, Benson, S. W. and ONeal,
H. E., National Standard Reference Data System,
U. S. Department of Commerce, National Bureau of
Standards, Washington, D.C. (1970) and assuming
a transmission coefficient of 1, calculate the
entropy of activation for this reaction at 750 K.