Chapter 3 Normative Analysis

1
Chapter 3 Normative Analysis
A. Welfare Economics of Pure Exchange - The
previous chapter dealt with the economic outcomes
of a policy. In this chapter, we develop the
notion of the desirability of a policy using the
tools of welfare economics. - We start with a
simple model, consisting of two people, Adam and
Eve, who consume two commodities, apples and fig
leaves, with fixed supplies, i.e. theres no
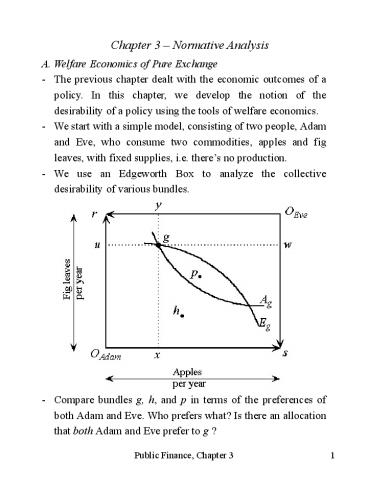
production. - We use an Edgeworth Box to analyze
the collective desirability of various bundles.
- Compare bundles g, h, and p in terms of the
preferences of both Adam and Eve. Who prefers
what? Is there an allocation that both Adam and
Eve prefer to g ?
2
- Note that by moving from g to p both
individuals can be made better off. In other
words, starting from allocation g, it is possible
to commit Pareto improvements. Indeed, starting
with an endowment, bargaining will provide such
improvements. - By definition, an allocation for
which no Pareto improvement is possible is Pareto
efficient. Then, we can say that g is not Pareto
efficient. How about p and h? The answer depends
on whether Pareto improvements are possible from
these points. - In the figure below, improvements
are not possible from p and h.
- The set of all Pareto efficient allocations is
depicted by a contract curve. - Note that at any
Pareto efficient allocation, indifference curves
are tangent to each other such that,
MRSafAdam MRSafEve
3
B. Production Economy - We now let productive
inputs to be shifted between producing apples and
fig leaves. - When inputs can be shifted and
provided that they are not wasted, increasing
apple production implies decreasing fig
production. The production possibilities curve
shows the maximum amount of fig leaves that can
be produced given any quantity of apples. - The
absolute value of the slope of the production
possibilities curve gives the marginal rate of
transformation of apples for fig leaves, which,
by definition, is equivalent to the ratio of
marginal costs - MRTaf gives the number of
fig leaves that could be produced by giving up a
unit of apple. Remember that MRSaf, on the other
hand, gives the number of fig leaves one would
require to give up one unit of apple. - Suppose
MRTaf 2 and MRSafAdam 1. Could Adam be made
better off ? - Provided that Adam has at least
one apple, he could give up one apple, which will
be transformed into two fig leaves. Since Adams
MRS is equivalent to unity, this transformation
would make him better off. - Nobody else is
worse off since only Adam gave up one apple and
gained two fig leaves.
4
- In fact we can find such Pareto improvements as
long as MRTaf differs from MRSaf for each person.
- Then, Pareto efficiency requires that
(1)
C. First Fundamental Theorem of Welfare
Economics - Let us now assume that, a) consumers
are perfectly informed and producers are
perfectly competitive profit-maximizers with no
market power, such that PX MCX for any product
X, and, b) a market exists for each and every
commodity. - As shown in the appendix for the
book, a consumer maximizes her utility by
choosing a bundle where the indifference curve is
tangent to the budget constraint - Also,
above we saw that profit maximization implies
that price equals marginal cost - Then, we can
see that the necessary condition for Pareto
efficiency in equation (1) is satisfied - Thus
, perfect competition leads to Pareto efficiency!
5
D. Fairness and Second Theorem of Welfare
Economics - Why need government if markets
allocate resources efficiently? - Markets are not
always competitive as required above. Market
power, externalities, information asymmetries
etc. may exist. Then, government intervention may
be necessary. - Perhaps more importantly, the
government may be interested in equity or
fairness. - Note that in the pure exchange model
in part A, the contract curve passes through the
origin for both Adam and Eve. This means that if
all goods are allocated to Adam or Eve, Pareto
efficiency is automatically satisfied! - More
generally, Adam and Eve can reach the contract
curve by bargaining. An important question is if
the government can redistribute the initial
endowments to achieve any point on the contract
curve. - The answer, both in the pure exchange
and the production economies, turns out to be
affirmative under some general conditions.