SemiClassical Methods and NBody Recombination

1
Semi-Classical Methods and N-Body
Recombination Seth RittenhouseITAMP,
Harvard-Smithsonian Center for Astrophysics,
Cambridge, MA 02138
Efimov States in Molecules and Nuclei, Oct. 21st
2009
2
Hard Problems with Simple Solutions Seth
Rittenhouse ITAMP, Harvard-Smithsonian Center
for Astrophysics, Cambridge, MA 02138
Efimov States in Molecules and Nuclei, Oct. 21st
2009
3
WKB is Smarter than You Think Seth Rittenhouse
ITAMP, Harvard-Smithsonian Center for
Astrophysics, Cambridge, MA 02138
Efimov States in Molecules and Nuclei, Oct. 21st
2009
4
(No Transcript)
5
Review of Recombination Experiments
2006 First solid evidence of an Efimov State was
seen in Innsbruck
6
Since then, several other groups have seen Efimov
states
Ottenstein et.al., PRL. 101, 203202 (2008)
Huckans et. al., PRL 102, 165302 (2009)
7
Since then, several other groups have seen Efimov
states
Zaccanti et. al., Nature Phys. 5, 586 (2009).
Ultra cold Li7 gas Rice group (soon to be
published)
8
More recently Four body effects have been
observed!
Ferlaino et. al., PRL 102, 140401 (2009)
Rice group
9
Hyperspherical Coordinates the first step for
easy few body scattering.

• General idea treat the
• hyperradius adiabatically
• (think Born-Oppenheimer).
• Provides us with a
• convenient view of the
• energy landscape

R
10
Hyperspherical Coordinates the first step for
easy few body scattering.

• General idea treat the
• hyperradius adiabatically
• (think Born-Oppenheimer).
• Provides us with a
• convenient view of the
• energy landscape

For example, The energy landscape 3 Bodies 2-D
R
11

• When the hyperradius is much different from all
  other
• length scales, the adiabatic potentials become
  universal, e.g.
• which is the non-interacting behavior at fixed
  hyperradius.
• The potentials for other length scale disparities
  look very
• similar, but with l non-integer valued or complex.

12
Relevant examples of potential curves
Three bosons with negative scattering length
13
Relevant examples of potential curves
Three bosons with negative scattering length
Transition region
Here be dragons!
Repulsive universal long-range tail
Attractive inner region
14
Relevant examples of potential curves
Four bosons with negative scattering length
15
Relevant examples of potential curves
Four bosons with negative scattering length
Repulsive four-body potentials
Broad avoided crossing
Efimov trimer threshold
Attractive inner wells
16
Not-so relevant examples of potential curves a
cautionary tale
Sometimes things can get ugly, so be careful!
17
Lets get quantitative
Once hyperradial potentials have been found, it
might be nice to have scattering crossections and
rate constants.
Three-body
Esry et. al., PRL 83, 1751 (1999) Fedichev et.
al., PRL 77, 2921 (1996) Nielsen and Macek,
PRL, 83 1566 (1999) Bedaque et. al., PRL 85, 908
(2000) Braaten and Hammer, PRL 87 160407 (2001)
and Phys. Rep. 428,259 (2006) Suno et. al., PRL
90, 053202 (2003).
18
Through some hyperspherical magic this can be
generalized to the N-body cross section and rate
Mehta, et. al., PRL 103, 153201 (2009)
This is messy, but there already is some good
physics buried in here.
19
At very low incident energies, only a single
incident channel survives. Using the unitary
nature of the S-matrix, this simplifies things
quite a bit
20
At very low incident energies, only a single
incident channel survives. Using the unitary
nature of the S-matrix, this simplifies things
quite a bit
This only depends on the incident channel!
If know about scattering in the initial channel,
then we know everything about the N-body losses!!!
Still a fairly nasty multi-channel problem, how
can we solve this?
21
WKB to the rescue
Specify a little bit more, consider N-bosons with
a negative two body scattering with at least one
weakly bound N-1 body state. The lowest N-body
channel will have a very generic form
22
Approximate the incident channel S-matrix element
using WKB phase shift with an imaginary component.
WKB phase inside the well
WKB tunneling
Imaginary phase (parameterizes losses)
23
Putting this all together gives the recombination
rate constant
24
Putting this all together gives the recombination
rate constant
25
Some things to note
This only holds when the coupling to deep
channels is with the scattering length. If
coupling exists at large R, we must go back to
the S-matrix, or find another cleaver way to
describe losses. This assumes the S matrix
element is completely controlled by the behavior
of the incoming channel. If outgoing channel is
important, as in recombination to weakly bound
dimers, a more sophisticated approximation of the
S-matrix is needed.
26
Re-examine three bosons
Assume that all of the tunneling occurs in the
universal large R region, and that all phase
accumulation occurs in the universal inner region.
27
Re-examine three bosons
Assume that all of the tunneling occurs in the
universal large R region, and that all phase
accumulation occurs in the universal inner region.
This gives a recombination rate constant of
In agreement with known results
28
A little discussion of four-boson potentials Von
Stecher et. al., Nature Phys. 5, pg 417
Look at potentials in this region. Negative
scattering length with at least one bound Efimov
state.
29
Just after first Efimov state becomes bound
Two four body bound states are attached to each
Efimov threshold.. (Hammer and Platter, Euro.
Phys. J. A 32, 113 von Stecher, DIncao and
Greene Nature Phys. 5, 417).
30
Slightly larger scattering length
31
Attractive region becomes deep enough to admit a
four-body state
32
Second Efimov state becomes bound. Two four-body
states can be supported for each Efimov state.
33
Applying the WKB Recombination formula
34
Applying the WKB Recombination formula
4-body resonances
Second Efimov state becomes bound. (Cusp?)
35
Can 4-body effects actually be seen? Surprisingly
, yes. Measurable four-body recombination occurs
to deeply bound dimer states (No weakly bound
trimers)
36
More recently Four body recombination to Efimov
Trimers has been measured.
37
Ngt4 Without potentials we cant say too much,
but recent work has shown where we could expect
resonances.
Can 5 or more body physics be seen,
38
Can 5 or more body physics be seen?
Without strong resonances, back of the envelope
approximation says, probably not.
39
Summary

• N-body recombination becomes intuitive when put
  into the adiabatic hyperspherical formalism
• Getting the potentials is hard, but even without
  them, scaling behavior can be extracted.
• Low energy recombination can be described by the
  scattering behavior in a single channel.
• WKB does surprisingly well in describing the
  single channel S-matrix
• Four body recombination can actually be measured
  in some regimes.

40
In 1970 a freshly-minted Russian PhD in
theoretical nuclear physics, Vitaly Efimov,
considered the following natural question What
is the nature of the bound state energy level
spectrum for a 3 particle system, when each of
its 2-particle subsystems have no bound states
but are infinitesimally close to binding?
Efimovs prediction There will be an INFINITE
number of 3-body bound states!!
This exponential factor 1/22.720.00194, i.e.
if one bound state is found at E0 -1 in some
system of units, then the next level will be
found at E1 -0.00194, and E2 -3.8 x 10-6, etc
.
41
The Efimov effect (restated) Nucl. Phys. A.
(1973)
42
Qualitative and quantitative understanding of
Efimovs result At a qualitative level, it can
be understood in hindsight, because two particles
that are already attracting each other and are
infinitesimally close to binding, just need a
whiff of additional attraction from a third
particle in order to push them over that
threshold to become a bound three-body
system. Quantitatively, Efimov (and later others)
showed that a simple wavefunction can be written
down at each hyperradius.
43
Lowest adiabatic hyperradial channel alt0
Short range stuff
Transition region
Universal region
Universal region
for identical bosons
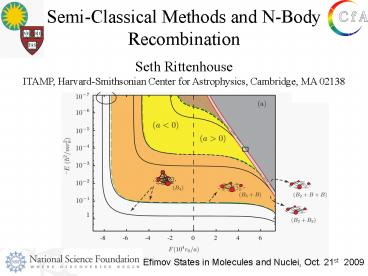
44
Observing the Efimov effect three-body
recombination
a lt 0
K.E.
45
Observing the Efimov effect three-body
recombination

• Three-body recombination can be measured through
  trap losses.
• Shape resonance occurs when an Efimov state
  appears at 0 energy.
• Spacing of shape resonances is geometric in the
  scattering length.

46

• Only one resonance, need two to show Efimov
  scaling
• Second resonance at
• Need low temperatures

47
Other possible Efimov states

• He trimer

48
Other possible Efimov states

• Recently, three hyperfine states of 6Li

Ottenstein et.al., PRL. 101, 203202 (2008)
Huckans et. al., arXiv0810.3288 (2008)
49
Real two-body interaction are multi-channel in
nature. Simplest thing Zero-range model
50
How does this translate to three bodies?
Start by looking at a simplified model no
coupling.
51
Parameters for an excited threshold resonance
Make excited bound state resonant with second
threshold
Coupled
Uncoupled
Coupled
52
Full calculation looks a bit ugly. First 300
potentials
PRA, 78 020701 (2008)
53
Simplified picture
Cartoon of two important curves.
Efimov Diabat
Efimov states

• Super-critical 1/R2 potential leads to
  geometrically spaced states.
• Coupling leads to quasi-stability Three-body
  Fano-Feshbach Resonances
• With no long-range coupling, widths scale
  geometrically

Actually an avoided crossing
Three free particles
54
The Experiment
Three particles come together at low energy with
respect to the first threshold.
Excite the system with RF photons.
If photon energy is degenerate with Efimov state
energy, expect strong coupling to lower channels.
Photon and binding energies are released as
kinetic energy
K.E.
K.E.
55
Cartoon three body loss spectrum.
1st state
2nd state
many states
56
Four Bosons and Efimovs legacy
Figure from von Stecher et. al., eprint
axiv/0810.3876
57
A little review of von Stechers work on
four-boson potentials eprint axiv/0810.3876
Look at potentials in this region. Negative
scattering length with at least one bound Efimov
state.
58
Just after first Efimov state becomes bound
59
Slightly larger scattering length
60
Attractive region becomes deep enough to admit a
four-body state
61
Second Efimov state becomes bound. Two four-body
states can be supported for each Efimov state.
62
Simplest way to see four-body physics is through
four-body recombination. N-body recombination
rate coefficient, in terms of the T matrix, is
given by
For four bosons in the low energy regime this
reduces to
63
The behavior T matrix element is dominated by the
lowest four-body channel.
64
If a four-body state is present, a shape
resonance occurs.
65
Using a simple WKB wavefunction gives the
four-body recombination rate coefficient up to an
overall factor.
4-body resonances
Second Efimov state becomes bound
a7 scaling (predicted by asymptotic scaling
potential)
66
Four-body behavior scales with the three-body
Efimov parameter. We can expect Log periodic
behavior!
Position of four-body resonances is universal
Observation of four-body resonances can give
another handle on identifying Efimov states
67
Summary

• 3-bodies and Efimov Physics PRA 78, 020701
  (2008)
• Zero-range multichannel interactions predict an
  Efimov potential at an excited three-body
  threshold.
• Coupling to lower channels gives bound states
  coupled to the three-body continuum 3-body
  Fano-Feshbach resonances!
• Quasi-stable Efimov states may, possibly, be
  accessed via RF spectroscopy allowing for the
  observation of multiple resonances.
• 4-bosons
• 4-body recombination shows universal resonance
  behavior.
• Postitions of 4-body resonances give a further
  handle on idetifying an Efimov state.

68
Four-Fermions
69
Jacobi and Democratic Hyperspherical Coordinates
Body-fixed democratic coodinates
(Aquilantii/Cavalli and Kuppermann)
70
Variational basis for four particles (Assume L0)
71
After just a few thousand cpu hours Potentials!
With potentials, we can start looking at
scattering
72
Dimer-dimer scattering length
With effective range
von Stecher, PRA (2008)
add (0) 0.6 a Petrov, PRL (2004)
73
Energy dependence means any finite collision
energy leads to deviation from the zero energy
results
74
What about dimer relaxation?
or
75
Unfortunately, there are an infinite number of
final states!
76
Fermis golden rule leads to a simple expression
for the rate
is the WKB tunneling probability
is the WKB wave number
is the density of final states near R
is probability that three particles are close
together at hyerradius R.
77
By performing the integral over different
hyperradial regions, we can isolate different
types of process.
Integration over only very small hyperradii
isolates relaxation channels where all four
particles are involved.
78
Three-body processes influenced by presence of
fourth particle
Four-body processes
Three-body only processes
79
Petrov (2004)
Small R contribution
Intermediate scaling behavior
arXiv0806.3062