Ratios and Proportion

1
Ratios and Proportion
ALGEBRA 1 LESSON 4-1
(For help, go to Skills Handbook pages 724 and
727.)
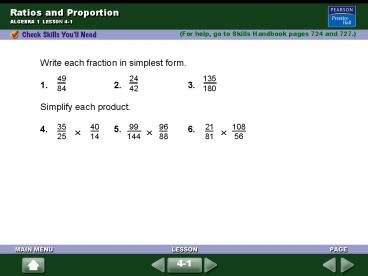
Write each fraction in simplest
form. 1. 2. 3. Simplify each
product. 4. 5. 6.
49 84
24 42
135 180
35 25
99 144
21 81
40 14
96 88
108 56
?
?
?
4-1
2
Ratios and Proportion
ALGEBRA 1 LESSON 4-1
1. 2. 3. 4. 5. 6.
Solutions
49 7 7 7 84 7 12 12


24 6 4 4 42 6 7 7


135 45 3 3 180 45 4 4


35 40 5 7 5 8 5 7 5 8 8 25 14 5 5 7
2 5 5 7 2 2
?
?



4
99 96 9 11 8 12 9 11 8 12 9
3 144 88 12 12 8 11 12 12 8 11 12 4
?
?




21 108 3 7 3 3 3 4 3 7 4
4 1 81 56 3 3 3 3 7 8 3 7 8
8 2
?
?
4




4
4-1
3
Ratios and Proportion
ALGEBRA 1 LESSON 4-1
Another brand of apple juice costs 1.56 for 48
oz. Find the unit rate.
The unit rate is 3.25/oz.
4-1
4
Ratios and Proportion
ALGEBRA 1 LESSON 4-1
The fastest recorded speed for an eastern gray
kangaroo is 40 mi per hour. What is the
kangaroos speed in feet per second?
The kangaroos speed is about 58.7 ft/s.
4-1
5
Ratios and Proportion
ALGEBRA 1 LESSON 4-1
y 3
3 4
Solve .
4-1
6
Ratios and Proportion
ALGEBRA 1 LESSON 4-1
w 4.5
6 5
Use cross products to solve the proportion
.
4-1
7
Ratios and Proportion
ALGEBRA 1 LESSON 4-1
In 2000, Lance Armstrong completed the 3630-km
Tour de France course in 92.5 hours. Traveling at
his average speed, how long would it take Lance
Armstrong to ride 295 km?
Traveling at his average speed, it would take
Lance approximately 7.5 hours to cycle 295 km.
4-1
8
Ratios and Proportion
ALGEBRA 1 LESSON 4-1
z 3 4
z 4 6
Solve the proportion .
4-1
9
Ratios and Proportion
ALGEBRA 1 LESSON 4-1
Solve. 1. Find the unit rate of a 12-oz bottle
of orange juice that sells for 1.29. 2. If you
are driving 65 mi/h, how many feet per second are
you driving? Solve each proportion. 3. 4.
5. 6.
10.75/oz.
about 95.3 ft/s
c 6
12 15
21 12
7 y
4.8
4


1 2
3 x 7
4 8
2 x x 4
25 35
17


4-1
10
Proportions and Similar Figures
ALGEBRA 1 LESSON 4-2
(For help, go to Skills Handbook and Lesson 4-1.)
Simplify 1. 2. 3. Solve each
proportion. 4. 5. 6. 7. 8. 9.
36 42
81 108
26 52
x 12
7 30
y 12
8 45
w 15
12 27



n 1 24
9 a
81 10
25 75
z 30
n 9



4-2
11
Proportions and Similar Figures
ALGEBRA 1 LESSON 4-2
1. 5. 7. 9. 2. 3. 4. 6. 8.
Solutions
y 12
8 45
9 a
81 10
n 9
n 1 24
36 42
6 6 6 6 7 7





45y 12(8)
81a 9(10)
24n 9(n 1)
81 108
27 3 3 27 4 4


45y 96
81a 90
24n 9n 9
26 52
26 1 1 26 2 2
15n 9


9 15
2 15
1 9
n
y 2
a 1
3 5
n
30x 12(7)
w 15
12 27
25 75
z 30


30x 84
27w 15(12)
75z 25(30)
27w 180
75z 750
2 3
w 6
z 10
4-2
12
Proportions and Similar Figures
ALGEBRA 1 LESSON 4-2
In the figure below, ABC DEF. Find AB.
AB is 12 mm.
4-2
13
Proportions and Similar Figures
ALGEBRA 1 LESSON 4-2
A flagpole casts a shadow 102 feet long. A 6 ft
tall man casts a shadow 17 feet long. How tall is
the flagpole?
The flagpole is 36 ft tall.
4-2
14
Proportions and Similar Figures
ALGEBRA 1 LESSON 4-2
The scale of a map is 1 inch 10 miles. The map
distance from Valkaria to Gifford is 2.25 inches.
Approximately how far is the actual distance?
The actual distance from Valkaria to Gifford is
approximately 22.5 mi.
4-2
15
Proportions and Similar Figures
ALGEBRA 1 LESSON 4-2
1. In the figure below, ABC DEF. Find
DF. 2. A boy who is 5.5 feet tall casts a
shadow that is 8.25 feet long. The tree next to
him casts a shadow that is 18 feet long. How
tall is the tree? 3. The scale on a map is 1
in. 20 mi. What is the actual distance between
two towns that are 3.5 inches apart on the map?
About 19.7 cm
12 ft
70 mi
4-2
16
Proportions and Percent Equations
ALGEBRA 1 LESSON 4-3
(For help, go to skills handbook pages 727 and
728.)
Find each product. 1. 0.6 9 2. 3.8
6.8 3. 4. Write each fraction as a decimal and
as a percent. 5. 6. 7. 8. 9. 10. 11. 12.
23 60
20 46
17 135
5 34


7 10
23 100
2 5
13 20
35 40
7 16
4 25
170 200
4-3
17
Proportions and Percent Equations
ALGEBRA 1 LESSON 4-3
1. 0.6 9 5.4 2. 3.8 6.8
25.84 3. 4. 5.
6. 7.
Solutions
23 60
20 46
23 20 20 3 23 2
1 3 2
1 6




17 135
5 34
17 5 5 27 17 2
1 27 2
1 54




7 10
7 10 0.7 0.7(100) 70
23 100
23 10 0.23 0.23(100) 23
2 5
2 5 0.4 0.4(100) 40
4-3
18
Proportions and Percent Equations
ALGEBRA 1 LESSON 4-3
Solutions (continued)
4-3
19
Proportions and Percent Equations
ALGEBRA 1 LESSON 4-3
What percent of 90 is 27?
30 of 90 is 27.
4-3
20
Proportions and Percent Equations
ALGEBRA 1 LESSON 4-3
Find 25 of 480.
25 of 480 is 120.
4-3
21
Proportions and Percent Equations
ALGEBRA 1 LESSON 4-3
Water covers about 361,736,000 km2, or about
70.8 of the earths surface area. Approximately
what is the total surface area of the earth?
The total surface area of the earth is
approximately 510,926,554 km2.
4-3
22
Proportions and Percent Equations
ALGEBRA 1 LESSON 4-3
What percent of 140 is 84?
140p 84
60 of 140 is 84.
4-3
23
Proportions and Percent Equations
ALGEBRA 1 LESSON 4-3
What percent of 60 is 144?
60n 114
190 of 60 is 114.
4-3
24
Proportions and Percent Equations
ALGEBRA 1 LESSON 4-3
a. Estimate the number that is 19 of 323.
b. What is 73 of 125? Use fractions to estimate
the answer.
93 is approximately 73 of 125.
4-3
25
Proportions and Percent Equations
ALGEBRA 1 LESSON 4-3
A candidate for mayor sent out surveys to 8056
people in his city. After two weeks, about 18 of
the surveys were returned. How many surveys were
returned?
n 0.18 8056
About 1450 surveys were returned.
4-3
26
Proportions and Percent Equations
ALGEBRA 1 LESSON 4-3
1. What is 35 of 160? 2. What percent of 450
is 36? 3. 32 is 80 of what number? 4. What
is 0.03 of 260,000? 5. What percent of 50 is
75? 6. Estimate 62 of 83?
56
8
40
78
150
51
4-3