MAC2233-1

1
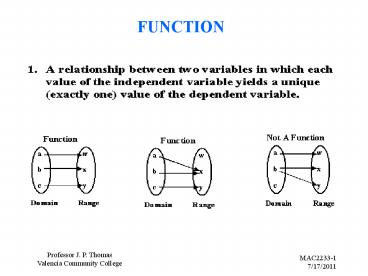
FUNCTION
2
DEFINITIONS
3
ALGEBRAIC FUNCTIONS
4
VERTICAL LINE TEST
5
LINEAR FUNCTIONS
f(x) mx b (Slope-intercept form)
y intercept
Independent variable
Slope
Dependent variable
ax by c 0 (General form)
(y2 - y1) m(x2 - x1) (Point slope form)
6
QUADRATIC FUNCTION
f(x) ax2 bx c
y intercept
Independent variable
Dependent variable
7
SKETCHING QUADRATIC FUNCTIONS
f(x)
f(x)
8
GENERAL SHAPE OF A POLYNOMIAL
9
VERTICAL ASYMPTOTES
10
HORIZONTAL ASYMPTOTES
11
EXPONENTIAL FUNCTION
y f(x) ax
Independent Variable x ? D
Base 0 lt a lt 1 Decreasing Function 1
lt a lt ? Increasing Function
Dependent Variable f(x) gt 0
Inverse Function Logarithmic Function
x log b y
12
EXPONENTIAL MODEL
P(t) P0 a t
Independent Variable t gt 0
Base 0 lt a lt 1 Decay Factor 1 lt a lt ?
Growth Factor
Initial Condition at t 0 P0 gt 0
Dependent Variable P(t) gt 0
13
LOGARITHMIC FUNCTIONS
COMMON LOGARITHMS
NATURAL LOGARITHMS
14
PROPERTIES OF LOGARITHMS
15
RATES OF CHANGE
Instantaneous Rate of Change Tangent Line
P2
Average Rate of Change Secant Line
P1
16
DIFFERENCE FUNCTIONS
Secant Line
17
BASIC ECONOMIC MODEL
Ct Cv Cf
Cost Function
Ct Total Cost Cv Variable cost nc n
number produced c unit cost of production Cf
Fixed Cost
Revenue Function
R np
n number sold p selling price
Profit Function
P R - Ct
18
BASIC ECONOMIC MODEL

Break Even Points
R
CT
Fixed Cost
P
n
19
INTEREST FORMULAE
20
LOGISTICS MODEL
LLimit of growth aconstant derived from
initial conditions kconstant derived from
boundary conditions ttime
21
DEFINITION OF A LIMIT
Left Hand Limit
Right Hand Limit
22
PROPERTIES OF LIMITS
1. For f(x) c (a constant),
2. For f(x) x,
23
LIMIT USING DIFFERENCE QUOTIENT
(xh. f(xh))
(x, f(x))
h
24
THE DERIVATIVE
The instantaneous rate of change of f(x) at x.
The slope of the tangent line to the graph of
f(x) at x
The limit of the difference equation as h (or ?x)
approaches 0.
25
FACTS ABOUT THE DERIVATIVE

• A derivative of a function, f(x), can be found
  for any value of x where the derivative exists.

• Since the derivative is a limit, then the limit
  must exist.

• The derivative itself is a function, f(x)

• When the derivative function, f(x), is
  evaluated at some value of xc, the resulting
  value is the slope of the line tangent to the
  original function at xc.

• When the derivative function, f(x), is
  evaluated at some value of xc, the resulting
  value is the instantaneous rate of change of the
  function, f(x), at xc.

26
DIFFERENTIATION
The process of determining the derivative of a
function is called differentiation.
27
RULES OF DIFFERENTIATION
1. Constant Function Rule
2. Power Function Rule
3. Constant Multiple Rule
4. Sum and Difference Rule
28
RULES OF DIFFERENTIATION (cont.)
5. Product Rule
6. Quotient Rule
29
FUNCTION DIFFERENTIABLE AT A POINT
30
DIFFERENTIALS
Since
Then
And
31
AVERAGE AND MARGINAL ANALYSIS
32
BASIC ECONOMIC MODEL

Break Even Points
R
CT
Fixed Cost
P
n
33
CHAIN RULE
34
PROPERTIES OF LOGARITHMS
35
DERIVATIVE OF LOGARITHMIC FUNCTION
Natural Logarithmic Function
General Logarithmic Function
36
DERIVATIVE OF EXPONENTIAL FUNCTION
Natural Exponential Function
General Exponential Function
37
IMPLICIT DIFFERENTIATION
Let f (x) y n
Since
Then
38
GRAPH DEFINITIONS
Absolute Maximum
P
Relative Maximum
P
P
I
P
c
c
c
c
c
c
Relative Minimum
P
P
Absolute Minimum
c critical value P critical point I
inflection point
39
Graphic Analysis 1
f(x)
f(x) 3x2 6x
cicritical value picritical point pici,
f(ci) Iinflection point
f(x) 6x 6
f(x) x3 3x2 - 4
x
c1 c2 P1
I p2
f(x) f(x) f(x) Concavity
Increasing ? Decreasing ? Increasing
gt0 0 lt 0 0 gt 0
lt0 0 gt0
Down ? Up
40
Graphic Analysis 2
f(x)
cicritical value picritical point pici,
f(ci) Iinflection point
f(x) .38x3 - 9.19x2 42.85x 1105
P1 I
p2 c1
c2
f(x) 2.28x 18.38
f(x) 1.14x2 18.38x 42.85
x
f(x) f(x) f(x) Concavity
Inc. ? Decreasing
? Increasing
gt0 0 lt 0
0 gt 0
lt0 0
gt0
Down ?
Up
41
Graphic Analysis 3
f(x)
f(x) 60x2 -20x3
cicritical value picritical point pici,
f(ci) Iinflection point
p2
I p1 c1
c2
f(x) 5x4 x5
x
f(x) 20x3 -5x4
f(x) f(x) f(x) Concavity
Decreasing ? Increasing ?
Decreasing
lt0 0 gt 0 0
lt 0
gt0 0 gt0 0 lt0
Up ? Up Down
42
GRAPHIC ANALYSIS AND CURVE SKETCHING

• Establish Dx.
• Find x and y intercepts, if possible
• Find end points.
• Find f(x)
• Find critical values f(x) 0.
• Find where f(x) is increasing f(x) gt 0 and
• decreasing f(x) lt 0.
• Locate extrema.
• Find f(x)
• Locate inflection points.
• Find where f(x) is concave up f(x) gt 0 and
• concave down f(x) lt 0.

43
Graphic Analysis 4
f(x)
cicritical value picritical point pici,
f(ci) Iinflection point
f(x) x 1 2x - 3
x
f(x) -1 . (2x 3)2
f(x) 4 . (2x 3)3
f(x) f(x) f(x) Concavity
Decreasing ? Decreasing
lt0 ?
lt0
lt0 ?
gt0
Down ?
Up
44
SKETCHING A GRAPH
P1 o

c1
f(x)
cicritical value picritical point pici,
f(ci) Iinflection point
I
f(x) .82x3 33.09x2 333.75x 435.28

o o
f(x) 4.92x 66.18
x
f(x) 2.46x2 66.18x 333.75
f(x) f(x) f(x) Concavity
Increasing ? Decreasing
gt0 0 lt 0
lt0 0 gt0
Down ? Up
45
SUMMARY OF FIRST DERIVATIVE

• f(x) is used to find
• Slope of tangent line at any point.
• Instantaneous rate of change.
• Critical values.
• Intervals of increasing f(x)
• Extrema

46
SUMMARY OF SECOND DERIVATIVE

• F(x) is used to find
• Increasing and decreasing behavior of the rate of
  change.
• Concavity of f(x).
• Direction of extrema, maximum or minimum.
• Inflection points f(x) 0.

47
SUMMARY OF GRAPHIC ANALYSIS AND CURVE SKETCHING
48
ANTIDERIVATIVE AND INDEFINATE INTEGRALS
49
INDEFINATE INTEGRAL FORMULAE
Power Rule For Antiderivatives
50
PROPERTIES OF INDEFINATE INTEGRALS
k dx k dx kx C
Constant Rule
51
AREA UNDER A CURVE
Right Sum
Left Sum
52
TRAPAZOIDAL RULE
1/2 0 5/4 1 9/8
1 1/2 2 5/4 13//8
3/2 1 13/4 2 21//8
2 3/2 5 13/4 31//8
53
DEFINITION OF THE INDEFINATE INTEGRAL
(over the interval a to b)
54
PROPERTIES OF DEFINATE INTEGRALS
55
FUNDAMENTAL THEOREM OF DEFINATE INTEGRALS
56
DISTANCE MODEL FOR A FALLING BODY
57
SUBSTUTUTION POWER RULE
n ? -1
58
TIPS ON u-SUBSTITUTION

• u is usually a radicand, a denominator, or an
  expression in parenthesis.
• Compute dx u du
• After the u-substitution into the integral, no
  factors can contain an x or other variable.
• Integrate
• Rewrite the antiderivative in terms of x, or the
  original independent variable.

59
INDEFINATE INTEGRAL FORMULAE
60
INTEGRATION BY PARTS
or
61
AREA BETWEEN CURVES
62
AREA BETWEEN TWO INTERSECTING CURVES
Compute the intersections of f(x) and g(x) to
find a and b
g(x)
b
x
a
f(x)
63
SUPPLY, DEMAND AND EQUILIBRIUM
Consumer Surplus
Producer Surplus
p - price
S(q) Supply Function
CS
Equilibrium Point
p1
PS
D(q) Demand Function
q - quantity
q1
64
AVERAGE VALUE FUNCTION
65
CONTINUOUS FLOW OF MONEY