1d Motion: Position

1
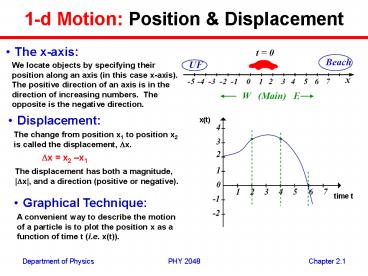
1-d Motion Position Displacement

• The x-axis

We locate objects by specifying their position
along an axis (in this case x-axis). The positive
direction of an axis is in the direction of
increasing numbers. The opposite is the negative
direction.

• Displacement

x(t)
The change from position x1 to position x2 is
called the displacement, Dx.
Dx x2 x1
The displacement has both a magnitude, Dx, and
a direction (positive or negative).
time t

• Graphical Technique

A convenient way to describe the motion of a
particle is to plot the position x as a function
of time t (i.e. x(t)).
2
1-d Motion Average Velocity

• Average Velocity

The average velocity is defined to be the
displacement, Dx, that occurred during a
particular interval of time, Dt (i.e. vave
Dx/Dt).

• Average Speed

The average speed is defined to be the magnitude
of total distance covered during a particular
interval of time, Dt (i.e. save (total
distance)/Dt).
3
1-d Motion Instantaneous Velocity
x
x(tDt)
x(t)
?
t
tDt
t
shrink Dt
Dt
4
1-d Motion Instantaneous Velocity
x
x(tDt)
x(t)
t
?
tDt
t
shrink Dt
Dt
5
1-d Motion Instantaneous Velocity
x
x(tDt)
x(t)
t
?
t
tDt
shrink Dt
Dt
6
1-d Motion Instantaneous Velocity
x
x(tDt)
x(t)
t
?
t
tDt
shrink Dt
Dt
7
1-d Motion Instantaneous Velocity
x
tangent line at t
x(t)
Instantaneous velocity v(t) is slope of x-t
tangent line at t
t
t
The velocity is the derivative of x(t) with
respect to t.
8
1-d Motion Acceleration

• Acceleration

When a particles velocity changes, the particle
is said to undergo acceleration (i.e. accelerate).

• Average Acceleration

The average acceleration is defined to be the
change in velocity, Dv, that occurred during a
particular interval of time, Dt (i.e. aave
Dv/Dt).

• Instantaneous Acceleration

v
The acceleration is the derivative of v(t) with
respect to t.
v(t)
Instantaneous acceleration a(t) is slope of v-t
tangent line at t
9
1-d Motion Summary

• Instantaneous Velocity

The velocity is the derivative of x(t) with
respect to t.

• Instantaneous Acceleration

The acceleration is the derivative of v(t) with
respect to t.

• Example Problem

The position of an object moving along the x-axis
is given by x(t) 3t 4t2 t3, where x is in
meters and t in seconds. What is the position,
velocity, and acceleration of the object at time
t 0?
10
Equations of Motion a constant

• Special case!

v at time t

• Integrate

v at t 0

• v varies linearly with time t

11
Equations of Motion a constant

• Special case!

x at time t

• Integrate

x at t 0

• x is a quadratic function of t

12
Equations of Motion a constant

• Special case! (constant acceleration)

v at t 0

• v is a linear function of t

• x is a quadratic function of t

x at t 0

• Note also that

13
Equations of Motion a 0

• Special case! (zero acceleration)

v at t 0

• v is constant

• x is a linear function of t

x at t 0
14
Equations of Motion Example Problem
15
Acceleration Due to Gravity

• Experimental Result

Near the surface of the Earth all objects fall
toward the center of the Earth with the same
constant acceleration, g 9.8 m/s2, (in a
vacuum) independent of mass, size, shape, etc.

• Equations of Motion

The acceleration due to gravity is almost
constant and equal to 9.8 m/s2 provided h ltlt RE!
16
Equations of Motion Example Problem
y-axis

• Example Problem

A ball is tossed up along the y-axis (in a vacuum
on the Earths surface) with an initial speed of
49 m/s.
vy0 49 m/s
Earth
How long does the ball take to reach its maximum
height?
What is the balls maximum height?
How long does it take for the ball to get back to
its starting point?
What is the velocity of the ball when it gets
back to its starting point?