When do Schafer and East play golf - PowerPoint PPT Presentation
1 / 15
Title:
When do Schafer and East play golf
Description:
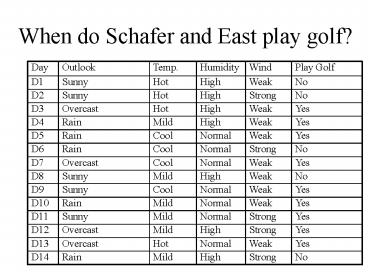
D12. Yes. Strong. Normal. Mild. Sunny. D11. Yes. Weak. Normal. Mild. Rain. D10. Yes. Weak. Normal ... Trivially, there exists a decision tree for any consistent ... – PowerPoint PPT presentation
Number of Views:55
Avg rating:3.0/5.0
Title: When do Schafer and East play golf
1
When do Schafer and East play golf?
2
Decision Tree for PlayGolf
Outlook
Sunny
Overcast
Rain
Humidity
Wind
Yes
High
Normal
Strong
Weak
No
Yes
Yes
No
3
Review Expressiveness of Decision Trees
- Decision trees can express ANY function of the
input attributes. - Trivially, there exists a decision tree for any
consistent training set (one path to a leaf for
each example). - But it probably wont generalize to new examples.
- We prefer to find more compact decision trees.
4
Review Think about it
- Which tree would you rather use
A
B
C
D
C
D
E
E
E
F
E
F
F
F
Y
Y
Y
Y
Y
N
Y
N
5
Review Think about it
- Which tree would you rather use
A
B
E
F
C
D
C
D
Y
A
B
E
N
Y
E
E
F
E
F
F
F
Y
Y
Y
Y
Y
N
Y
N
6
Decision tree learning
- The question is
- How do you select a small tree consistent with
the training examples? - Idea (recursively) choose the most significant
attribute as root of (sub)tree.
7
ID3 and Entropy
- ID3 is an example of a decision tree learning
algorithm. - ID3 builds the decision tree from the top down,
selecting the features from the training data
that provide the most information at each stage. - It is built on the concept of Entropy or chaos
in the system
8
Entropy
- S is a sample of training examples
- p is the proportion of positive examples
- p- is the proportion of negative examples
- Entropy measures the impurity of S
- Entropy(S) -p log2 p - p- log2 p-
9
Entropy
- The entropy of S is zero when all the examples
are positive, or when all the examples are
negative. - Entropy(S) -p log2 p - p- log2 p-
- Entropy(S) -1 (log2 1) - 0 (log2 0)
- Entropy(S) 0
10
Entropy
- The entropy reaches its maximum value of 1 when
exactly half of the examples are positive, and
half are negative. - Entropy(S) -p log2 p - p- log2 p-
- Entropy(S) -0.5 log2 0.5 - 0.5 log2 0.5
- Entropy(S) -0.5 (-1) - 0.5 (-1)
- Entropy(S) 1
11
What is the Entropy at the start of our Do they
golf problem?
- How is the data split??
- Nine positive cases
- Five negative cases
- Entropy(S) -p log2 p - p- log2 p-
- Entropy(S) -9/14 (log2 9/14) 5/14 (log2 5/14)
- Entropy(S) -0.643 (-0.637) 0.357 (-1.485)
- Entropy(S) 0.940
12
ID3 and Entropy
- ID3 selects attributes based on information gain.
- Information gain is the reduction in entropy
caused by a decision.
13
Which Attribute is best?
14
Top-Down Induction of Decision Trees ID3
- A ? the best decision attribute for next node
- Assign A as decision attribute for node
- For each value of A create new descendant
- Sort training examples to leaf node according to
- the attribute value of the branch
- If all training examples are perfectly classified
(same value of target attribute) stop, else
iterate over new leaf nodes.
15
Lets use ID3 to develop the golf decision tree