LotkaVolterra Competition Model - PowerPoint PPT Presentation
1 / 24
Title:
LotkaVolterra Competition Model
Description:
Understand the development of the Lotka-Volterra model of competition ... Growth Pattern, beginning as exponential growth and reaching an asymptote at K. ... – PowerPoint PPT presentation
Number of Views:1294
Avg rating:3.0/5.0
Title: LotkaVolterra Competition Model
1
Lotka-Volterra Competition Model
2
Lecture Goals
- Understand the development of the Lotka-Volterra
model of competition - State the underlying assumptions of the model
- Summarize the predictions of the model
- Describe the estimation of competition
coefficients
3
dN/dt r N ( K- N)/K
4
K
5
What if there are 2 species (Species1 and
Species2) with identical limits and rates
(population parameters)?
NTot N1 N2
dN1/dt r N1 (K - NTot) / K)
Similar for dN2/dt ...
6
What if K differs for each species (K1 K2)?
dN1/dt r N1 (K1 - NTot) / K1)
dN2/dt ?
dN2/dt r N2 (K2 - NTot) / K2)
7
What if r also differs between species?
dN1/dt r1 N1 (K1 - NTot) / K1)
dN2/dt ?
dN2/dt r2 N2 (K2 - NTot) / K2)
Competition is still represented in the common
effect on K1 K2 through NTot.
8
What if Species 1 2 are unequal in their impact
on resources?
Effective N for each K is no longer simply N1
N2 NTot!
a12 is the competitive equivalence of Species2 on
the population growth of Species1.
9
So for Species1
dN1/dt r1 N1 (K1 - NTot) / K1)
And similarly for Species2, so that we can model
a 2 species system with competition as ...
10
The Lotka-Volterra Competition Model
11
Competition Coefficients
Each additional Species1 individual has the same
impact on Species1's resources as a12 individuals
of Species2.
What about a21?
12
Review of Assumptions
- Builds upon the Logistic, thus
- all individuals identical (average)
- asexual reproduction (females)
- no imm/em/igration (low net rate)
- continuous reproduction/mortality (remember
discrete form too) - intraspecific competition causes birth and death
rate to vary with population size (how?) - Also in Lotka-Volterra Model of Competition
- interspecific competition limiting population
growth of each species through influence birth
and death rates reflected in population
parameters(r, K, ...) - gtgtgt Still a very simplified model
13
Isoclines and Predictions
14
Plotting 2 Species Population Dynamics
15
Defining Isoclines
When there is no Change in Species1 Abundance
dN1/dt 0, because N1 is constant
16
(No Transcript)
17
N2 (K1 / a12) - (1/a12) N1
defines a straight line that crosses the N2
axis at ? , and which has a slope equal to ? .
This is the N1 isocline. The N2 isocline is
similarly defined.
18
(No Transcript)
19
(No Transcript)
20
Model Predictions
- The model predicts, for different parameters and
initial conditions, the presence of both - coexistence
- exclusion
- For a particular case, parameters must be
estimated to make predictions.
21
How can you estimate a12?
- Grow Species1 alone to estimate r1 and K1
- fit the logistic equation to observed population
growth - Grow Species1 Species2 together
- IF THEY coexist at equilibrium (dN1/dt dN2/dt
0) - Neq? N? at equilibrium
a12 (K1 - Neq1)/Neq2
(Similar for a21)
22
What About Predictions Prior toEquilibrium/Extinc
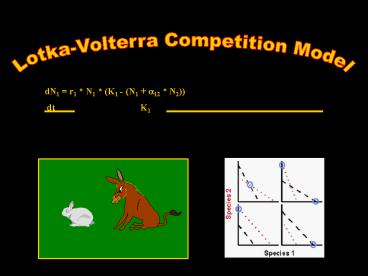
tion?
dNi ri Ni (Ki - (Ni aij Nj)) dt
Ki
23
Crombie (1945) tested the Lotka-Volterra model of
competition by estimating the competition
coefficients for two coexisting beetles and then
examining the predictions of the model for
consistency with the observation.
We will briefly duplicate this now...
24
Questions for Consideration
- What are the qualitative predictions of the
Lotka-Volterra competition model? Is this model
'adequate? Why or why not? - What biological factors may contribute to
observed values of a? - Francisco Ayala fitted the Lotka-Volterra model
to 2 Drosophila spp., and found that the model
predicted exclusion of one spp. however,
coexistence was observed. How does this influence
our view of competition? (Nature 2241076,
Science 171820).