The Fourier Transform

1
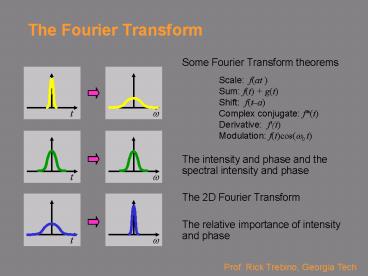
The Fourier Transform

• Some Fourier Transform theorems
• Scale f(at )
• Sum f(t) g(t)
• Shift f(ta)
• Complex conjugate f(t)
• Derivative f'(t)
• Modulation f(t)cos(w0 t)
• The intensity and phase and the spectral
  intensity and phase
• The 2D Fourier Transform
• The relative importance of intensity and phase

Prof. Rick Trebino, Georgia Tech
2
The Fourier Transform and its Inverse
3
Scale Theorem

• The Fourier transform of a scaled function,
  f(at)

Proof
Assuming a gt 0, change variables u at, so
dt du / a
If a lt 0, the limits flip when we change
variables, introducing a minus sign, hence the
absolute value.
4
The Scale Theorem in action
f(t)
F(w)
Shortpulse
The shorter the pulse, the broader the spectrum!
Medium-lengthpulse
This is the essence of the Uncertainty Principle!
Longpulse
5
The Fourier Transform of a sum of two functions
f(t)
F(w)
w
t
g(t)
G(w)
w
t
F(w) G(w)
f(t)g(t)
Also, constants factor out. The Fourier transform
is a linear function of functions.
w
t
6
Shift Theorem
7
Application of the Shift Theorem

• Suppose were measuring the spectrum of E(t), but
  a small fraction of its irradiance, say e, takes
  a longer path to the spectrometer.
• The extra light has the field, ve E(ta), where
  a is the extra path.
• The measured spectrum is

Performing the Fourier Transform and using the
Shift Theorem
8
Application of the Shift Theorem (contd)

• Neglecting e compared to ve and 1
• The contaminated spectrum will have ripples with
  a period of 2p/a.
• And these ripples will have a surprisingly large
  amplitude.

If e 1 (a seemingly small amount), these
ripples will have an amazing-ly large amplitude
of 2ve 20! And peak-to-peak, theyre 40!
9
The Fourier Transform of the complex conjugate of
a function
Proof
10
Negative frequencies contain no additional
information for real functions.
If a function is real (e.g., a light wave!), then
f(t) f(t). So
Using the result we just proved
So, at w, the real part of the Fourier transform
of f is the same as at w. And the imaginary
part is just the negative of it.
11
Derivative Theorem

• The Fourier transform of a derivative of a
  function, f(t)
•  
•  
• Proof
• Integrate by parts

Remember that the function must be zero at 8, so
the other term, f(t) exp(-iwt) vanishes.
8
-8
12
The Modulation TheoremThe Fourier Transform of
E(t) cos(w0 t)
Example
E(t) exp(-t2)
t
w
w0
-w0
0
13
The Fourier transform and its inverse are
symmetrical f(t) F(w) and F(t) f(w) (almost).
If f(t) Fourier transforms to F(w), then F(t)
Fourier transforms to
Rearranging
Relabeling the integration variable from t to w,
we can see that we have an inverse Fourier
transform
This is why it is often said that f and F are a
Fourier Transform Pair.
14
Fourier Transform Magnitude and Phase

• As with any complex quantity, we can decompose
  f(t) and F(w) into their magnitude and phase.
• f(t) can be written f(t) Magf(t) exp -i
  Phasef(t)
• where Magf(t)2 is often called the intensity,
  I(t), and Phasef(t) is called the phase, f(t).
  Theyre the same quantities were used to for
  light waves (the minus signs are arbitrary).
• Analogously, F(w) MagF(w) exp -i
  PhaseF(w)
• The MagF(w)2 is called the spectrum, S(w), and
  the PhaseF(w) is called the spectral phase,
  j(w).
• Just as both the intensity and phase are required
  to specify f(t), both the spectrum and spectral
  phase are required to specify F(w), and hence
  f(t).

15
Light has intensity and phase also.
We usually extract out the carrier frequency.
A light wave has the time-domain electric field
Intensity
Phase
The minus signs are just conventions.
(neglecting the negative-frequency component)
Equivalently, vs. frequency
Spectral
Spectrum
Phase
Knowledge of the intensity and phase or the
spectrum and spectral phase is sufficient to
determine the light wave.
16
Calculating the Intensity and the Phase
Its easy to go back and forth between the
electric field and the intensity and phase. The
intensity
I(t) E(t)2
The phase
E(ti)
Im
vI(ti)
-f(ti)
Re
Equivalently,
f(t) -Im lnE(t)?
We can do the same for the field in the frequency
domain.
17
Complex Lorentzianand its Intensity and Phase
a
Real
component
0
0
Imaginary
component
w
Real part
Imag part
18
Intensity and phase of a decaying exponential and
its Fourier transform
exp(-2at)
Time domain Frequency domain
(solid)
19
Intensity and Phase of a Gaussian

• The Gaussian is real, so its phase is zero.

Time domain Frequency domain
A Gaussian transforms to a Gaussian
So the spectral phase is zero, too.
20
The spectral phase of a time-shifted pulse
Recall the Shift Theorem
Time-shifted Gaussian pulse (with a flat phase)
So a time-shift simply adds some linear spectral
phase to the pulse!
21
What is the spectral phase anyway?
Its the absolute phase of each frequency in the
wave-form.
All of these frequencies have zero phase. So this
pulse has j(w) 0 Note that this wave-form
sees constructive interference, and hence peaks,
at t 0. And it has cancellation everywhere
else.
w1 w2 w3 w4 w5 w6
0
22
Now try a linear spectral phase j(w) aw.
By the Shift Theorem, a linear spectral phase is
just a delay in time. And this is what occurs!
w1 w2 w3 w4 w5 w6
j(w1) 0
j(w2) 0.2 p
j(w3) 0.4 p
j(w4) 0.6 p
j(w5) 0.8 p
j(w6) p
t
23
The spectral phase distinguishes a light bulb
from a short pulse.
Intensity vs. time
Intensity vs. time
24
Fourier Transform with respect to space
If f(x) is a function of position,

• F f(x) F(k)

We refer to k as the spatial frequency. Everythin
g weve said about Fourier transforms between the
t and w domains also applies to the x and k
domains.
25
The 2D Fourier Transform

• F (2)f(x,y) F(kx,ky)
• f(x,y) exp-i(kxxkyy) dx dy
• If f(x,y) fx(x) fy(y),
• then the 2D FT splits into two 1D FT's.
• But this doesnt always happen.

F (2)f(x,y)
26
A 2D Fourier Transform a square function

• Consider a square function in the xy plane
• f(x,y) rect(x) rect(y)
• The 2D Fourier Transform splits into the product
  of two 1D Fourier Transforms
• F f(x,y) sinc(kx/2) sinc(ky/2)
• This picture is an optical determination
• of the Fourier Transform of the
• square function!

F (2)f(x,y)
27
Fourier Transform Magnitude and Phase
Pictures reconstructed using the spectral
phase of the other picture
MagF Linda PhaseF Rick
MagF Rick PhaseF Linda
The phase of the Fourier transform (spectral
phase) is much more important than the magnitude
in reconstructing an image.