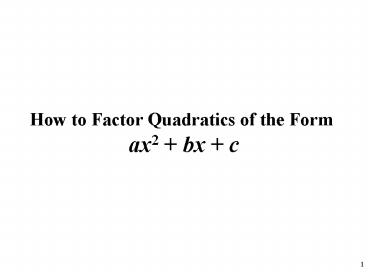How to Factor Quadratics of the Form

1
How to Factor Quadratics of the Form ax2 bx c
2
The first rule of thumb in factoring is to factor
out, if any, the greatest common factor of all
the terms, for example 1. 2x2 6x 8 2(x2
3x 4) 2. 5x3 20x2 15x 5x(x2 4x 3)
On the other hand, what if the expression has no
common factors? For example, x2 4x 2 and x2
4x 3. Keep in mind that not all quadratic
expression can be factored. Our first example x2
4x 2 is not factorable (in this case, the
expression is called a prime). The second
example, however, x2 4x 3 can be factored as
(x 1)(x 3).
3
There are a couple of ways we can determine
whether a quadratic expression is factorable or
not. We will show you some of those ways later.
But first, we are going to show you how to factor
any quadratic expressions if they are indeed
factorable. We will divide these quadratic
expressions into two classes 1. x2 bx c,
that is, a 1, and 2. ax2 bx c, where a ? 1
4
Lets look at some of the examples in the first
class and see how to factor them 1. x2 5x
6 2. x2 7x 10 3. x2 2x 15 4. x2 6x
16 If they are factorable, each of them must be
factored as (x )(x ) since that is the
only way x2 can be factored. How about the two
numbers that should be also in the
parentheseshow do we get them? Those two numbers
can be obtained by asking, What two numbers
multiplied will give me the last term? Lets
repeat this againwhat two numbers multiply, not
add. There are two pairs of numbers that multiply
to be 6, 1, 6 and 2, 3, and for 10, 1, 10
and 2, 5, and for 15, 1, 15 and 3, 5
whereas 16 has three pairs 1, 16, 2, 8, and
4, 4. Which pair should we use?
5
1. x2 5x 6 2. x2 7x 10 3. x2 2x 15
4. x2 6x 16 Actually, it is quite easy to
choose the right pair of numbers that multiply to
be the last term. This is how If the last term
is positive, like in the first two examples, ask
what two numbers multiplied is the last term and
their sum is the coefficient of the middle
term If the last term is negative, like in the
last two examples, ask what two numbers
multiplied is the last term and their difference
is the coefficient of the middle term. Here, you
can ignore the sign of the coefficient of the
middle term. That is, just consider it is
positive even if it is negative.
6
1. x2 5x 6 2. x2 7x 10 3. x2 2x 15
4. x2 6x 16 If you understood what we said
on the previous page, you should have picked 2,
3, 2, 5, 3, 5, and 2, 8 for our four
examples, respectively. That is, you should have
written something like the following 1. x2 5x
6 (x 2)(x 3) 2. x2 7x 10 (x
2)(x 5) 3. x2 2x 15 (x 3)(x 5)
4. x2 6x 16 (x 2)(x 8)
7
1. x2 5x 6 (x 2)(x 3) 2. x2 7x 10
(x 2)(x 5) 3. x2 2x 15 (x 3)(x
5) 4. x2 6x 16 (x 2)(x 8) How should
we determine the sign between the x and the
number? If the last term is positive, then both
signs should be the same and they follow the sign
of the coefficient of the middle term, i.e., if
that coefficient is a) positive, then both
signs should be , the plus sign b) negative,
then both signs should be , the minus sign. If
the last term is negative and then one sign
should be and the other is and if the
coefficient of the middle term is a) positive,
then put with the larger number and with
the smaller number b) negative, then put
with the larger number and with the
smaller number.
8

• If you followed what we said on the previous
  page, you should have factored the quadratic
  expressions as follows
• 1. x2 5x 6 (x 2)(x 3) 2. x2 7x 10
  (x 2)(x 5)
• 3. x2 2x 15 (x 3)(x 5) 4. x2 6x
  16 (x 2)(x 8)
• If you think the rules on the previous two pages
  are more than you can handle at this time, no
  problemwe have an easier way for you to factor
  quadratic expressions like the ones above. All
  you need to do is ask
• What are the two numbers that
• if I multiply, they will give me the last term,
  and
• if I add or subtract, they will give me the
  coefficient of the middle term.
• Again, ignore the signs of the the last term and
  the coefficient of the middle term (we always can
  take care of the signs later).

9
Lets look at the following example x2 2x 24
Recall the last term, 24, is obtained by
multiplying. The only two numbers that can add or
subtract to be 2 in the middle term are 4 and 6.
Therefore, we can forget about the other pairs
that also multiply to 24, namely, 1, 24, 2,
12, and 3, 8. You will have at least this x2
2x 24 (x 4)(x 6) What about the
signs? Since we obtain 24 by multiplying and its
sign is minus, so one sign must be (plus) and
the other must be (minus). So, just put the
signs in. x2 2x 24 (x 4)(x 6) Are you
puzzled? What happen if we put the with the 6
and the with the 4will that work too?
10
The answer is no, it will not work. Thats why we
should always check whether we have the signs (if
they are different) in the right place or not. To
see whether x2 2x 24 is really equal to (x
4)(x 6), some text books would suggest to FOIL
(x 4)(x 6) (i.e., to multiply it out) and see
if it is equal to x2 2x 24. (x 4)(x 6)
x2 6x 4x 24 x2 2x 24 Therefore, its
the correct factoring, but a waste of time. We
obviously know the F will give us the first
term, x2, and L will give us the last term,
24. Therefore, we only need to check I (the
inner terms) and O (the outer terms).
F
O
I
L
11
(x 4)(x 6) Combine the inner and outer
products by adding, the result is 2x, which is
exactly the middle term of x2 2x 24.
Therefore, the factoring must be correct. If,
unfortunately, you have factored x2 2x 24 as
(x 4)(x 6), you can still check it by the
method mentioned above. (x 4)(x 6) Again,
combine the inner and outer products, the result
is 2x. Although its not the 2x we want to
have, it is exactly the opposite. In this case,
just switch the two signs, i.e., change (x
4)(x 6) to (x 4)(x 6). It will be correct,
with 100 guarantee, you dont have to check it
again.
12
Lets look at the following example x2 13x
30 In this case, we seem to have two pairs of
numbers 2, 15 and 3, 10 which will work,
since each pair has a product of 30 and while the
difference of first pair is 13, the sum of the
second pair is also 13. So which pair? Why not
write both out and see which is the correct pair?
Again, dont write the signs yet. (x 2)(x 15)
(x 3)(x 10) We see 30 has a sign. In
order to have the sign by multiplying, either
both signs have to be or both be . Since
the 13 also has a sign, the signs must both
be . Put in the signs, we can see only (x
3)(x 10) is correct (x 2)(x 15) (x
3)(x 10)
Yes!
No!
13

• If you have been following what we have said so
  far, it is quite easy to determine whether a
  quadratic expression is factorable or not. For
  example, the following quadratic expressions are
  not factorable
• 1. x2 6x 24
• 2. x2 11x 24
• 3. x2 5x 24
• The first one is not factorable since 6 (the
  coefficient of the middle term) is neither the
  sum nor the difference of any desirable pairs of
  factors of 24.
• The second one is also not factorable since the
  last term is 24 we want the difference of the
  two factors of 24 to be 11, but 11 is not one of
  such differences.
• The last one is also not factorable since the
  last term is 24 we want the sum of the two
  factors of 24 to be 5, but 5 is not one of such
  sums.

14
We have one more trick which we call the closer
factors trick. When the last term has more than
one desirable pair of factors, usually it is the
pair of factors that are close to each other or
the pair(s) that are in the times table. For
example, if the last term is 42, it is likely the
pair (which gives a product of 42) is 6, 7,
more so than 3, 14, 2, 21 and 1, 42. If the
last term is 24, it is most likely a toss-up
between 4, 6 and 3, 8, rather than a toss-up
between 2, 12 and 1, 24. Although this trick
will not be always the case, it is very probable.
Its even more probable for quadratic expressions
of the form ax2 bx c where a ? 1. We are
going to discuss this type of quadratic
expressions next.
15
Now, lets look at the following example 4x2
4x 15. In order to obtain the first term, 4x2
(by multi-plying), we must use either 2x and 2x
or x and 4x. To get the last term, 15 (also by
multiplying), we must use either 3 and 5 or 1
and 15. This can be quite a hassle, because it
could be one of the six factor forms shown on
the right. Which one? We cant really tell you
which one is right, but we can tell you that you
should always try the one with the factors that
are closer to each other first (recall the
closer factors trick we have mentioned
earlier). Therefore, try (2x 3)(2x 5) first.
Check inner and outer products again and see if
it really works. The inner product gives 6x
while the outer gives 10x. Since the15 of the
last term has a sign, so the signs must be
one and the other . Therefore, if we
place the sign with the 5 and with the
3, we will have 10x and 6x which will combine
to 4x. So, 4x2 4x 15 (2x 3)(2x 5).
16
Lets look at this example 6x2 23x 20. If
you are following the closer factors trick, you
should have something like (2x 5)(3x 4) or
(2x 4)(3x 5). Lets look at the second choice
(2x 4)(3x 5), notice that you can factor out
a 2 from (2x 4). However, the original
expression 6x2 23x 20 has no common factor.
Therefore, it cant be (2x 4)(3x 5). We call
this the no common factor trick. That is,
make sure that the numbers appearing in the
same parenthesis have no common factor if the
given expression has no common factor. Lets go
back to (2x 5)(3x 4) and see if it really
works. We see that the inner product gives 15x
and the outer gives 8x and we see that the 20 of
the last term has a sign and the 23 of the
middle term also has a sign, so the signs
must be both . So, 6x2 23x 20 (2x
5)(3x 4).
17
Here is another example 6x2 7x 24. Using
the closer factors tactic, you would have (2x
)(3x ) for the 6x2, and the closest pair that
gives a product of 24 is 4 and 6. In which
parenthesis should you put the 4 and the 6? The
answer is neitherdont put either number in. It
is be-cause it breaks the no common factor
rule. The next closest pair that gives a product
of 24 is 3 and 8. Again, in which paren-thesis
should you put the 3 and the 8? The answer is to
put the 3 with 2x and the 8 with 3x, i.e., (2x
3)(3x 8). The inner product of (2x 3)(3x
8) gives 9x while the outer gives 16x. And its
only possible to obtain the 7x (the mid-dle
term) if we assign the sign with 8 and the
with 3 (see illustration on the right).
Therefore, 6x2 7x 24 (2x 3)(3x 8).
18
By using the closer factors and no common
factor tricks wisely (especially the latter
one), its quite easy to determine whether the
quadratic expression is factorable or not. For
example, its not difficult to see that 6x2
11x 48 is not factorable by using these two
tactics. If you have (3x )(2x ), notice
that you cant put in any pairs of factors of 48
into (3x )(2x ), because one way or another
they all break the no common factor rule. Our
last resort is (6x )(x ). We can see that
every pair break the rule except the last pair 1
and 48. And we must put 1 with the 6x and 48
with x and see if it works. When we multiply the
inner terms and the outer terms, however, we
will have 288x and 1x which can never become
11x of the middle term. So, 6x2 11x 48 is
not factorable.
19

• We can also determine whether a quadratic
  expression of the form ax2 bx c is factorable
  or not by checking whether b2 4ac (1) is a
  perfect square or not. If the result is a perfect
  square (2), then the quadratic expression is
  factorable otherwise, it is not. Our example 6x2
  11x 48 has a 6, b 11 and c 48. In this
  case, however, b2 4ac 112 4(6)(48) is
  negativeit cant be a perfect square.
• Therefore, 6x2 11x 48 is not factorable.
• Notes
• 1. b2 4ac is called the discriminant of ax2
  bx c.
• 2. A perfect square (including 0) is a number
  that is the square of some integer. Hence, the
  perfect squares are 0, 1, 4, 9, 16, 25, etc.

20

• Many areas in algebra requires the knowledge of
  factoring quadratics. These include
• Solving most quadratic equations,
• Solving rational equations,
• Simplifying rational expressions, and last but
  not least,
• Solving trigonometric, logarithmic, exponential
  and higher-degree equations which are really
  quadratic equations in disguise.

Quadratic Equations
Rational Equations
x2 5x 6 0 2x2 x 3 0 3x2 4x 7 4x2
3 4x
Rational Expressions
Others
x4 10x2 9 0 sin2x 2sin x 3 0 e2x
7ex 12 0 (log x)2 4log x 5 0