DUMMY VARIABLE CLASSIFICATION WITH TWO CATEGORIES - PowerPoint PPT Presentation
1 / 159
Title:
DUMMY VARIABLE CLASSIFICATION WITH TWO CATEGORIES
Description:
This sequence explains how you can include qualitative explanatory variables in ... In words, our null hypothesis is that there is no difference in the overhead ... – PowerPoint PPT presentation
Number of Views:51
Avg rating:3.0/5.0
Title: DUMMY VARIABLE CLASSIFICATION WITH TWO CATEGORIES
1
DUMMY VARIABLE CLASSIFICATION WITH TWO CATEGORIES
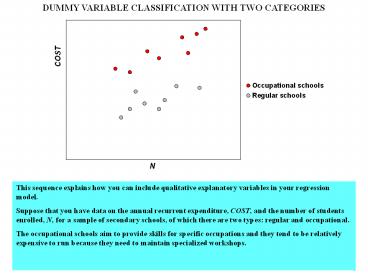
This sequence explains how you can include
qualitative explanatory variables in your
regression model. Suppose that you have data on
the annual recurrent expenditure, COST, and the
number of students enrolled, N, for a sample of
secondary schools, of which there are two types
regular and occupational. The occupational
schools aim to provide skills for specific
occupations and they tend to be relatively
expensive to run because they need to maintain
specialized workshops.
1
2
DUMMY VARIABLE CLASSIFICATION WITH TWO CATEGORIES
One way of dealing with the difference in the
costs would be to run separate regressions for
the two types of school. However this would have
the drawback that you would be running
regressions with two small samples instead of one
large one, with an adverse effect on the
precision of the estimates of the coefficients.
5
3
DUMMY VARIABLE CLASSIFICATION WITH TWO CATEGORIES
b1'
b1
OCC 0 Regular school COST b1 b2N u OCC
1 Occupational school COST b1' b2N u
Another way of handling the difference would be
to hypothesize that the cost function for
occupational schools has an intercept b1' that is
greater than that for regular schools.
6
4
DUMMY VARIABLE CLASSIFICATION WITH TWO CATEGORIES
b1'
b1
OCC 0 Regular school COST b1 b2N u OCC
1 Occupational school COST b1' b2N u
Effectively, we are hypothesizing that the annual
overhead cost is different for the two types of
school, but the marginal cost is the same. The
marginal cost assumption is not very plausible
and we will relax it in due course.
7
5
DUMMY VARIABLE CLASSIFICATION WITH TWO CATEGORIES
b1'
d
b1
OCC 0 Regular school COST b1 b2N u OCC
1 Occupational school COST b1' b2N u
Let us define d to be the difference in the
intercepts d b1' - b1.
8
6
DUMMY VARIABLE CLASSIFICATION WITH TWO CATEGORIES
b1d
d
b1
OCC 0 Regular school COST b1 b2N u OCC
1 Occupational school COST b1 d b2N u
Then b1' b1 d and we can rewrite the cost
function for occupational schools as shown.
9
7
DUMMY VARIABLE CLASSIFICATION WITH TWO CATEGORIES
b1d
d
b1
Combined equation COST b1 d OCC b2N u OCC
0 Regular school COST b1 b2N u OCC 1
Occupational school COST b1 d b2N u
We can now combine the two cost functions by
defining a dummy variable OCC that has value 0
for regular schools and 1 for occupational
schools.
10
8
DUMMY VARIABLE CLASSIFICATION WITH TWO CATEGORIES
b1d
d
b1
Combined equation COST b1 d OCC b2N u OCC
0 Regular school COST b1 b2N u OCC 1
Occupational school COST b1 d b2N u
Dummy variables always have two values, 0 or 1.
If OCC is equal to 0, the cost function becomes
that for regular schools. If OCC is equal to 1,
the cost function becomes that for occupational
schools.
11
9
DUMMY VARIABLE CLASSIFICATION WITH TWO CATEGORIES
We will now fit a function of this type using
actual data for a sample of 74 secondary schools
in Shanghai.
12
10
DUMMY VARIABLE CLASSIFICATION WITH TWO CATEGORIES
School Type COST N OCC 1 Occupationa
l 345,000 623 1 2 Occupational
537,000 653 1 3 Regular 170,000 400 0 4 Occupa
tional 526.000 663 1 5 Regular 100,000 563 0 6
Regular 28,000 236 0 7 Regular
160,000 307 0 8 Occupational 45,000 173 1 9 Oc
cupational 120,000 146 1 10 Occupational 61,00
0 99 1
The table shows the data for the first 10 schools
in the sample. The annual cost is measured in
yuan, one yuan being worth about 20 cents U.S. at
the time. N is the number of students in the
school. OCC is the dummy variable for the type of
school.
13
11
DUMMY VARIABLE CLASSIFICATION WITH TWO CATEGORIES
. reg COST N OCC Source SS df
MS Number of obs
74 ---------------------------------------
F( 2, 71) 56.86 Model
9.0582e11 2 4.5291e11 Prob gt
F 0.0000 Residual 5.6553e11 71
7.9652e09 R-squared
0.6156 ---------------------------------------
Adj R-squared 0.6048 Total
1.4713e12 73 2.0155e10 Root
MSE 89248 ------------------------------
------------------------------------------------
COST Coef. Std. Err. t
Pgtt 95 Conf. Interval ----------------
--------------------------------------------------
----------- N 331.4493 39.75844
8.337 0.000 252.1732 410.7254 OCC
133259.1 20827.59 6.398 0.000
91730.06 174788.1 _cons -33612.55
23573.47 -1.426 0.158 -80616.71
13391.61 -----------------------------------------
-------------------------------------
We now run the regression of COST on N and OCC,
treating OCC just like any other explanatory
variable, despite its artificial nature. The
Stata output is shown. We will begin by
interpreting the regression coefficients.
15
12
DUMMY VARIABLE CLASSIFICATION WITH TWO CATEGORIES
Regular School (OCC
0)
COST -34,000 133,000OCC 331N
COST -34,000 331N
The regression results have been rewritten in
equation form. From it we can derive cost
functions for the two types of school by setting
OCC equal to 0 or 1. If OCC is equal to 0, we get
the equation for regular schools, as shown. It
implies that the marginal cost per student per
year is 331 yuan and that the annual overhead
cost is -34,000 yuan. Obviously having a negative
intercept does not make any sense at all and it
suggests that the model is misspecified in some
way. We will come back to this later.
18
13
DUMMY VARIABLE CLASSIFICATION WITH TWO CATEGORIES
Regular School (OCC
0) Occupational School (OCC 1)
COST -34,000 133,000OCC 331N
COST -34,000 331N
COST -34,000 133,000 331N
99,000 331N
The coefficient of the dummy variable is an
estimate of d, the extra annual overhead cost of
an occupational school. Putting OCC equal to 1,
we estimate the annual overhead cost of an
occupational school to be 99,000 yuan. The
marginal cost is the same as for regular schools.
It must be, given the model specification.
21
14
DUMMY VARIABLE CLASSIFICATION WITH TWO CATEGORIES
The scatter diagram shows the data and the two
cost functions derived from the regression
results.
22
15
DUMMY VARIABLE CLASSIFICATION WITH TWO CATEGORIES
. reg COST N OCC Source SS df
MS Number of obs
74 ---------------------------------------
F( 2, 71) 56.86 Model
9.0582e11 2 4.5291e11 Prob gt
F 0.0000 Residual 5.6553e11 71
7.9652e09 R-squared
0.6156 ---------------------------------------
Adj R-squared 0.6048 Total
1.4713e12 73 2.0155e10 Root
MSE 89248 ------------------------------
------------------------------------------------
COST Coef. Std. Err. t
Pgtt 95 Conf. Interval ----------------
--------------------------------------------------
----------- N 331.4493 39.75844
8.337 0.000 252.1732 410.7254 OCC
133259.1 20827.59 6.398 0.000
91730.06 174788.1 _cons -33612.55
23573.47 -1.426 0.158 -80616.71
13391.61 -----------------------------------------
-------------------------------------
We will perform a t test on the coefficient of
the dummy variable. Our null hypothesis is H0 d
0 and our alternative hypothesis is H1 d
0. In words, our null hypothesis is that there is
no difference in the overhead costs of the two
types of school. The t statistic is 6.40, so it
is rejected at the 0.1 significance level.
24
16
DUMMY VARIABLE CLASSIFICATION WITH TWO CATEGORIES
. reg COST N OCC Source SS df
MS Number of obs
74 ---------------------------------------
F( 2, 71) 56.86 Model
9.0582e11 2 4.5291e11 Prob gt
F 0.0000 Residual 5.6553e11 71
7.9652e09 R-squared
0.6156 ---------------------------------------
Adj R-squared 0.6048 Total
1.4713e12 73 2.0155e10 Root
MSE 89248 ------------------------------
------------------------------------------------
COST Coef. Std. Err. t
Pgtt 95 Conf. Interval ----------------
--------------------------------------------------
----------- N 331.4493 39.75844
8.337 0.000 252.1732 410.7254 OCC
133259.1 20827.59 6.398 0.000
91730.06 174788.1 _cons -33612.55
23573.47 -1.426 0.158 -80616.71
13391.61 -----------------------------------------
-------------------------------------
We can perform t tests on the other coefficients
in the usual way. The t statistic for the
coefficient of N is 8.34, so we conclude that the
marginal cost is (very) significantly different
from 0.
26
17
DUMMY VARIABLE CLASSIFICATION WITH TWO CATEGORIES
. reg COST N OCC Source SS df
MS Number of obs
74 ---------------------------------------
F( 2, 71) 56.86 Model
9.0582e11 2 4.5291e11 Prob gt
F 0.0000 Residual 5.6553e11 71
7.9652e09 R-squared
0.6156 ---------------------------------------
Adj R-squared 0.6048 Total
1.4713e12 73 2.0155e10 Root
MSE 89248 ------------------------------
------------------------------------------------
COST Coef. Std. Err. t
Pgtt 95 Conf. Interval ----------------
--------------------------------------------------
----------- N 331.4493 39.75844
8.337 0.000 252.1732 410.7254 OCC
133259.1 20827.59 6.398 0.000
91730.06 174788.1 _cons -33612.55
23573.47 -1.426 0.158 -80616.71
13391.61 -----------------------------------------
-------------------------------------
In the case of the intercept, the t statistic is
-1.43, so we do not reject the null hypothesis
H0 b1 0. Thus one explanation of the
nonsensical negative overhead cost of regular
schools might be that they do not actually have
any overheads and our estimate is a random
number. A more realistic version of this
hypothesis is that b1 is positive but small (as
you can see, the 95 percent confidence interval
includes positive values) and the error term is
responsible for the negative estimate. As already
noted, a further possibility is that the model is
misspecified in some way. We will continue to
develop the model in the next sequence.
27
18
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
COST b1 dTTECH dWWORKER dVVOC b2N
u
This sequence explains how to extend the dummy
variable technique to handle a qualitative
explanatory variable which has more than two
categories. In the previous sequence we used a
dummy variable to differentiate between regular
and occupational schools when fitting a cost
function. In actual fact there are two types of
regular secondary school in Shanghai. There are
general schools, which provide the usual academic
education, and vocational schools.
1
19
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
COST b1 dTTECH dWWORKER dVVOC b2N
u
As their name implies, the vocational schools are
meant to impart occupational skills as well as
give an academic education. However the
vocational component of the curriculum is
typically quite small and the schools are similar
to the general schools. Often they are just
general schools with a couple of workshops
added. Likewise there are two types of
occupational school. There are technical schools
training technicians and skilled workers schools
training craftsmen.
4
20
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
COST b1 dTTECH dWWORKER dVVOC b2N
u
So now the qualitative variable has four
categories. The standard procedure is to choose
one category as the reference category and to
define dummy variables for each of the others. In
general it is good practice to select the most
normal or basic category as the reference
category, if one category is in some sense more
normal or basic than the others. In the Shanghai
sample it is sensible to choose the general
schools as the reference category. They are the
most numerous and the other schools are
variations of them.
7
21
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
COST b1 dTTECH dWWORKER dVVOC b2N
u
Accordingly we will define dummy variables for
the other three types. TECH will be the dummy
for the technical schools TECH is equal to 1 if
the observation relates to a technical school, 0
otherwise. Similarly we will define dummy
variables WORKER and VOC for the skilled workers
schools and the vocational schools.
10
22
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
COST b1 dTTECH dWWORKER dVVOC b2N
u
Each of the dummy variables will have a
coefficient which represents the extra overhead
costs of the schools, relative to the reference
category. Note that you do not include a dummy
variable for the reference category, and that is
the reason that the reference category is usually
described as the omitted category.
12
23
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
COST b1 dTTECH dWWORKER dVVOC b2N
u General School COST b1 b2N u (TECH
WORKER VOC 0)
If an observation relates to a general school,
the dummy variables are all 0 and the regression
model is reduced to its basic components.
14
24
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
COST b1 dTTECH dWWORKER dVVOC b2N
u General School COST b1 b2N u (TECH
WORKER VOC 0) Technical School COST
(b1 dT) b2N u (TECH 1 WORKER VOC
0)
If an observation relates to a technical school,
TECH will be equal to 1 and the other dummy
variables will be 0. The regression model
simplifies as shown.
15
25
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
COST b1 dTTECH dWWORKER dVVOC b2N
u General School COST b1 b2N u (TECH
WORKER VOC 0) Technical School COST
(b1 dT) b2N u (TECH 1 WORKER VOC
0) Skilled Workers School COST (b1 dW)
b2N u (WORKER 1 TECH VOC 0) Vocational
School COST (b1 dV) b2N u (VOC 1
TECH WORKER 0)
The regression model simplifies in a similar
manner in the case of observations relating to
skilled workers schools and vocational schools.
16
26
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
COST
Technical
dT
dW
b1dT
Workers
b1dW
Vocational
dV
b1dV
General
b1
N
The diagram illustrates the model graphically.
The d coefficients are the extra overhead costs
of running technical, skilled workers, and
vocational schools, relative to the overhead cost
of general schools.
17
27
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
COST
Technical
dT
dW
b1dT
Workers
b1dW
Vocational
dV
b1dV
General
b1
N
Note that we do not make any prior assumption
about the size, or even the sign, of the d
coefficients. They will be estimated from the
sample data.
18
28
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
The scatter diagram shows the data for the entire
sample, differentiating by type of school.
20
29
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
. reg COST N TECH WORKER VOC Source
SS df MS Number of
obs 74 -----------------------------------
---- F( 4, 69) 29.63
Model 9.2996e11 4 2.3249e11
Prob gt F 0.0000 Residual 5.4138e11
69 7.8461e09 R-squared
0.6320 ---------------------------------------
Adj R-squared 0.6107 Total
1.4713e12 73 2.0155e10 Root
MSE 88578 ------------------------------
------------------------------------------------
COST Coef. Std. Err. t
Pgtt 95 Conf. Interval ----------------
--------------------------------------------------
----------- N 342.6335 40.2195
8.519 0.000 262.3978 422.8692 TECH
154110.9 26760.41 5.759 0.000
100725.3 207496.4 WORKER 143362.4
27852.8 5.147 0.000 87797.57
198927.2 VOC 53228.64 31061.65
1.714 0.091 -8737.646 115194.9 _cons
-54893.09 26673.08 -2.058 0.043
-108104.4 -1681.748 ----------------------------
--------------------------------------------------
Here is the Stata output for this regression.
The coefficient of N indicates that the marginal
cost per student per year is 343 yuan.
21
30
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
. reg COST N TECH WORKER VOC Source
SS df MS Number of
obs 74 -----------------------------------
---- F( 4, 69) 29.63
Model 9.2996e11 4 2.3249e11
Prob gt F 0.0000 Residual 5.4138e11
69 7.8461e09 R-squared
0.6320 ---------------------------------------
Adj R-squared 0.6107 Total
1.4713e12 73 2.0155e10 Root
MSE 88578 ------------------------------
------------------------------------------------
COST Coef. Std. Err. t
Pgtt 95 Conf. Interval ----------------
--------------------------------------------------
----------- N 342.6335 40.2195
8.519 0.000 262.3978 422.8692 TECH
154110.9 26760.41 5.759 0.000
100725.3 207496.4 WORKER 143362.4
27852.8 5.147 0.000 87797.57
198927.2 VOC 53228.64 31061.65
1.714 0.091 -8737.646 115194.9 _cons
-54893.09 26673.08 -2.058 0.043
-108104.4 -1681.748 ----------------------------
--------------------------------------------------
The coefficients of TECH, WORKER, and VOC are
154,000, 143,000, and 53,000, respectively, and
should be interpreted as the additional annual
overhead costs, relative to those of general
schools.
22
31
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
. reg COST N TECH WORKER VOC Source
SS df MS Number of
obs 74 -----------------------------------
---- F( 4, 69) 29.63
Model 9.2996e11 4 2.3249e11
Prob gt F 0.0000 Residual 5.4138e11
69 7.8461e09 R-squared
0.6320 ---------------------------------------
Adj R-squared 0.6107 Total
1.4713e12 73 2.0155e10 Root
MSE 88578 ------------------------------
------------------------------------------------
COST Coef. Std. Err. t
Pgtt 95 Conf. Interval ----------------
--------------------------------------------------
----------- N 342.6335 40.2195
8.519 0.000 262.3978 422.8692 TECH
154110.9 26760.41 5.759 0.000
100725.3 207496.4 WORKER 143362.4
27852.8 5.147 0.000 87797.57
198927.2 VOC 53228.64 31061.65
1.714 0.091 -8737.646 115194.9 _cons
-54893.09 26673.08 -2.058 0.043
-108104.4 -1681.748 ----------------------------
--------------------------------------------------
The constant term is -55,000, indicating that the
annual overhead cost of a general academic school
is -55,000 yuan per year. Obviously this is
nonsense and indicates that something is wrong
with the model.
23
32
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
COST -55,000 154,000TECH 143,000WORKER
53,000VOC 343N
The top line shows the regression result in
equation form. We will derive the implicit cost
functions for each type of school.
24
33
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
COST -55,000 154,000TECH 143,000WORKER
53,000VOC 343N General School COST -55,000
343N (TECH WORKER VOC 0)
In the case of a general school, the dummy
variables are all 0 and the equation reduces to
the intercept and the term involving N.
25
34
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
COST -55,000 154,000TECH 143,000WORKER
53,000VOC 343N General School COST -55,000
343N (TECH WORKER VOC 0)
The annual marginal cost per student is estimated
at 343 yuan. The annual overhead cost per school
is estimated at -55,000 yuan. Obviously a
negative amount is inconceivable.
26
35
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
COST -55,000 154,000TECH 143,000WORKER
53,000VOC 343N General School COST -55,000
343N (TECH WORKER VOC 0) Technical
School COST -55,000 154,000 343N (TECH 1
WORKER VOC 0) 99,000 343N
The extra annual overhead cost for a technical
school, relative to a general school, is 154,000
yuan. Hence we derive the implicit cost function
for technical schools.
27
36
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
COST -55,000 154,000TECH 143,000WORKER
53,000VOC 343N General School COST -55,000
343N (TECH WORKER VOC 0) Technical
School COST -55,000 154,000 343N (TECH 1
WORKER VOC 0) 99,000 343N Skilled
Workers School COST -55,000 143,000
343N (WORKER 1 TECH VOC 0) 88,000
343N Vocational School COST -55,000 53,000
343N (VOC 1 TECH WORKER 0) -2,000
343N
And similarly the extra overhead costs of skilled
workers and vocational schools, relative to
those of general schools, are 143,000 and 53,000
yuan, respectively.
28
37
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
COST -55,000 154,000TECH 143,000WORKER
53,000VOC 343N General School COST -55,000
343N (TECH WORKER VOC 0) Technical
School COST -55,000 154,000 343N (TECH 1
WORKER VOC 0) 99,000 343N Skilled
Workers School COST -55,000 143,000
343N (WORKER 1 TECH VOC 0) 88,000
343N Vocational School COST -55,000 53,000
343N (VOC 1 TECH WORKER 0) -2,000
343N
Note that in each case the annual marginal cost
per student is estimated at 343 yuan. The model
specification assumes that this figure does not
differ according to type of school.
29
38
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
The four cost functions are illustrated
graphically.
30
39
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
. reg COST N TECH WORKER VOC Source
SS df MS Number of
obs 74 -----------------------------------
---- F( 4, 69) 29.63
Model 9.2996e11 4 2.3249e11
Prob gt F 0.0000 Residual 5.4138e11
69 7.8461e09 R-squared
0.6320 ---------------------------------------
Adj R-squared 0.6107 Total
1.4713e12 73 2.0155e10 Root
MSE 88578 ------------------------------
------------------------------------------------
COST Coef. Std. Err. t
Pgtt 95 Conf. Interval ----------------
--------------------------------------------------
----------- N 342.6335 40.2195
8.519 0.000 262.3978 422.8692 TECH
154110.9 26760.41 5.759 0.000
100725.3 207496.4 WORKER 143362.4
27852.8 5.147 0.000 87797.57
198927.2 VOC 53228.64 31061.65
1.714 0.091 -8737.646 115194.9 _cons
-54893.09 26673.08 -2.058 0.043
-108104.4 -1681.748 ----------------------------
--------------------------------------------------
We can perform t tests on the coefficients in the
usual way. The t statistic for N is 8.52, so the
marginal cost is (very) significantly different
from 0, as we would expect.
31
40
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
. reg COST N TECH WORKER VOC Source
SS df MS Number of
obs 74 -----------------------------------
---- F( 4, 69) 29.63
Model 9.2996e11 4 2.3249e11
Prob gt F 0.0000 Residual 5.4138e11
69 7.8461e09 R-squared
0.6320 ---------------------------------------
Adj R-squared 0.6107 Total
1.4713e12 73 2.0155e10 Root
MSE 88578 ------------------------------
------------------------------------------------
COST Coef. Std. Err. t
Pgtt 95 Conf. Interval ----------------
--------------------------------------------------
----------- N 342.6335 40.2195
8.519 0.000 262.3978 422.8692 TECH
154110.9 26760.41 5.759 0.000
100725.3 207496.4 WORKER 143362.4
27852.8 5.147 0.000 87797.57
198927.2 VOC 53228.64 31061.65
1.714 0.091 -8737.646 115194.9 _cons
-54893.09 26673.08 -2.058 0.043
-108104.4 -1681.748 ----------------------------
--------------------------------------------------
The t statistic for the technical school dummy is
5.76, indicating the the annual overhead cost of
a technical school is (very) significantly
greater than that of a general school, again as
expected.
32
41
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
. reg COST N TECH WORKER VOC Source
SS df MS Number of
obs 74 -----------------------------------
---- F( 4, 69) 29.63
Model 9.2996e11 4 2.3249e11
Prob gt F 0.0000 Residual 5.4138e11
69 7.8461e09 R-squared
0.6320 ---------------------------------------
Adj R-squared 0.6107 Total
1.4713e12 73 2.0155e10 Root
MSE 88578 ------------------------------
------------------------------------------------
COST Coef. Std. Err. t
Pgtt 95 Conf. Interval ----------------
--------------------------------------------------
----------- N 342.6335 40.2195
8.519 0.000 262.3978 422.8692 TECH
154110.9 26760.41 5.759 0.000
100725.3 207496.4 WORKER 143362.4
27852.8 5.147 0.000 87797.57
198927.2 VOC 53228.64 31061.65
1.714 0.091 -8737.646 115194.9 _cons
-54893.09 26673.08 -2.058 0.043
-108104.4 -1681.748 ----------------------------
--------------------------------------------------
Similarly for skilled workers schools, the t
statistic being 5.15.
33
42
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
. reg COST N TECH WORKER VOC Source
SS df MS Number of
obs 74 -----------------------------------
---- F( 4, 69) 29.63
Model 9.2996e11 4 2.3249e11
Prob gt F 0.0000 Residual 5.4138e11
69 7.8461e09 R-squared
0.6320 ---------------------------------------
Adj R-squared 0.6107 Total
1.4713e12 73 2.0155e10 Root
MSE 88578 ------------------------------
------------------------------------------------
COST Coef. Std. Err. t
Pgtt 95 Conf. Interval ----------------
--------------------------------------------------
----------- N 342.6335 40.2195
8.519 0.000 262.3978 422.8692 TECH
154110.9 26760.41 5.759 0.000
100725.3 207496.4 WORKER 143362.4
27852.8 5.147 0.000 87797.57
198927.2 VOC 53228.64 31061.65
1.714 0.091 -8737.646 115194.9 _cons
-54893.09 26673.08 -2.058 0.043
-108104.4 -1681.748 ----------------------------
--------------------------------------------------
In the case of vocational schools, however, the t
statistic is only 1.71, indicating that the
overhead cost of such a school is not
significantly greater than that of a general
school. This is not surprising, given that the
vocational schools are not much different from
the general schools. Note that the null
hypotheses for the tests on the coefficients of
the dummy variables are than the overhead costs
of the other schools are not different from those
of the general schools.
34
43
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
. reg COST N TECH WORKER VOC Source
SS df MS Number of
obs 74 -----------------------------------
---- F( 4, 69) 29.63
Model 9.2996e11 4 2.3249e11
Prob gt F 0.0000 Residual 5.4138e11
69 7.8461e09 R-squared
0.6320 ---------------------------------------
Adj R-squared 0.6107 Total
1.4713e12 73 2.0155e10 Root
MSE 88578 ------------------------------
------------------------------------------------
COST Coef. Std. Err. t
Pgtt 95 Conf. Interval ----------------
--------------------------------------------------
----------- N 342.6335 40.2195
8.519 0.000 262.3978 422.8692 TECH
154110.9 26760.41 5.759 0.000
100725.3 207496.4 WORKER 143362.4
27852.8 5.147 0.000 87797.57
198927.2 VOC 53228.64 31061.65
1.714 0.091 -8737.646 115194.9 _cons
-54893.09 26673.08 -2.058 0.043
-108104.4 -1681.748 ----------------------------
--------------------------------------------------
Finally we will perform an F test of the joint
explanatory power of the dummy variables as a
group. The null hypothesis is H0 dT dW dV
0. The alternative hypothesis is that at least
one d is different from 0.
37
44
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
. reg COST N TECH WORKER VOC Source
SS df MS Number of
obs 74 -----------------------------------
---- F( 4, 69) 29.63
Model 9.2996e11 4 2.3249e11
Prob gt F 0.0000 Residual 5.4138e11
69 7.8461e09 R-squared
0.6320 ---------------------------------------
Adj R-squared 0.6107 Total
1.4713e12 73 2.0155e10 Root
MSE 88578 ------------------------------
------------------------------------------------
COST Coef. Std. Err. t
Pgtt 95 Conf. Interval ----------------
--------------------------------------------------
----------- N 342.6335 40.2195
8.519 0.000 262.3978 422.8692 TECH
154110.9 26760.41 5.759 0.000
100725.3 207496.4 WORKER 143362.4
27852.8 5.147 0.000 87797.57
198927.2 VOC 53228.64 31061.65
1.714 0.091 -8737.646 115194.9 _cons
-54893.09 26673.08 -2.058 0.043
-108104.4 -1681.748 ----------------------------
--------------------------------------------------
Finally we will perform an F test of the joint
explanatory power of the dummy variables as a
group. The null hypothesis is H0 dT dW dV
0. The alternative hypothesis is that at least
one d is different from 0. The residual sum of
squares in the specification including the dummy
variables is 5.411011.
38
45
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
. reg COST N Source SS df
MS Number of obs
74 ---------------------------------------
F( 1, 72) 46.82 Model
5.7974e11 1 5.7974e11 Prob gt
F 0.0000 Residual 8.9160e11 72
1.2383e10 R-squared
0.3940 ---------------------------------------
Adj R-squared 0.3856 Total
1.4713e12 73 2.0155e10 Root
MSE 1.1e05 ------------------------------
------------------------------------------------
COST Coef. Std. Err. t
Pgtt 95 Conf. Interval ----------------
--------------------------------------------------
----------- N 339.0432 49.55144
6.842 0.000 240.2642 437.8222 _cons
23953.3 27167.96 0.882 0.381
-30205.04 78111.65 ----------------------------
--------------------------------------------------
The residual sum of squares in the specification
excluding the dummy variables is 8.921011.
39
46
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
. reg COST N Source SS df
MS Number of obs
74 ---------------------------------------
F( 1, 72) 46.82 Model
5.7974e11 1 5.7974e11 Prob gt
F 0.0000 Residual 8.9160e11 72
1.2383e10 R-squared
0.3940 ---------------------------------------
Adj R-squared 0.3856 Total
1.4713e12 73 2.0155e10 Root
MSE 1.1e05 . reg COST N TECH WORKER
VOC Source SS df MS
Number of obs 74 ---------------
------------------------ F( 4,
69) 29.63 Model 9.2996e11 4
2.3249e11 Prob gt F
0.0000 Residual 5.4138e11 69 7.8461e09
R-squared 0.6320 -------------
-------------------------- Adj
R-squared 0.6107 Total 1.4713e12 73
2.0155e10 Root MSE 88578
The reduction in RSS when we include the dummies
is therefore (8.92 - 5.41)1011. We will check
whether this reduction is significant with the
usual F test.
40
47
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
. reg COST N Source SS df
MS Number of obs
74 ---------------------------------------
F( 1, 72) 46.82 Model
5.7974e11 1 5.7974e11 Prob gt
F 0.0000 Residual 8.9160e11 72
1.2383e10 R-squared
0.3940 ---------------------------------------
Adj R-squared 0.3856 Total
1.4713e12 73 2.0155e10 Root
MSE 1.1e05 . reg COST N TECH WORKER
VOC Source SS df MS
Number of obs 74 ---------------
------------------------ F( 4,
69) 29.63 Model 9.2996e11 4
2.3249e11 Prob gt F
0.0000 Residual 5.4138e11 69 7.8461e09
R-squared 0.6320 -------------
-------------------------- Adj
R-squared 0.6107 Total 1.4713e12 73
2.0155e10 Root MSE 88578
The numerator in the F ratio is the reduction in
RSS divided by the cost, which is the 3 degrees
of freedom given up when we estimate three
additional coefficients (the coefficients of the
dummies).
41
48
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
. reg COST N Source SS df
MS Number of obs
74 ---------------------------------------
F( 1, 72) 46.82 Model
5.7974e11 1 5.7974e11 Prob gt
F 0.0000 Residual 8.9160e11 72
1.2383e10 R-squared
0.3940 ---------------------------------------
Adj R-squared 0.3856 Total
1.4713e12 73 2.0155e10 Root
MSE 1.1e05 . reg COST N TECH WORKER
VOC Source SS df MS
Number of obs 74 ---------------
------------------------ F( 4,
69) 29.63 Model 9.2996e11 4
2.3249e11 Prob gt F
0.0000 Residual 5.4138e11 69 7.8461e09
R-squared 0.6320 -------------
-------------------------- Adj
R-squared 0.6107 Total 1.4713e12 73
2.0155e10 Root MSE 88578
The denominator is RSS for the specification
including the dummy variables, divided by the
number of degrees of freedom remaining after they
have been added. The F ratio is therefore 14.92.
42
49
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
. reg COST N Source SS df
MS Number of obs
74 ---------------------------------------
F( 1, 72) 46.82 Model
5.7974e11 1 5.7974e11 Prob gt
F 0.0000 Residual 8.9160e11 72
1.2383e10 R-squared
0.3940 ---------------------------------------
Adj R-squared 0.3856 Total
1.4713e12 73 2.0155e10 Root
MSE 1.1e05 . reg COST N TECH WORKER
VOC Source SS df MS
Number of obs 74 ---------------
------------------------ F( 4,
69) 29.63 Model 9.2996e11 4
2.3249e11 Prob gt F
0.0000 Residual 5.4138e11 69 7.8461e09
R-squared 0.6320 -------------
-------------------------- Adj
R-squared 0.6107 Total 1.4713e12 73
2.0155e10 Root MSE 88578
F tables do not give the critical value for 3 and
69 degrees of freedom, but it must be lower than
the critical value with 3 and 60 degrees of
freedom. This is 6.17, at the 0.1 significance
level.
44
50
DUMMY CLASSIFICATION WITH MORE THAN TWO CATEGORIES
. reg COST N Source SS df
MS Number of obs
74 ---------------------------------------
F( 1, 72) 46.82 Model
5.7974e11 1 5.7974e11 Prob gt
F 0.0000 Residual 8.9160e11 72
1.2383e10 R-squared
0.3940 ---------------------------------------
Adj R-squared 0.3856 Total
1.4713e12 73 2.0155e10 Root
MSE 1.1e05 . reg COST N TECH WORKER
VOC Source SS df MS
Number of obs 74 ---------------
------------------------ F( 4,
69) 29.63 Model 9.2996e11 4
2.3249e11 Prob gt F
0.0000 Residual 5.4138e11 69 7.8461e09
R-squared 0.6320 -------------
-------------------------- Adj
R-squared 0.6107 Total 1.4713e12 73
2.0155e10 Root MSE 88578
Thus we reject H0 at a high significance level.
This is not exactly surprising since t tests show
that TECH and WORKER have highly significant
coefficients.
45
51
THE EFFECTS OF CHANGING THE REFERENCE CATEGORY
In the previous sequence we chose general
academic schools as the reference (omitted)
category and defined dummy variables for the
other categories. This enabled us to compare the
overhead costs of the other schools with those of
general schools and to test whether the
differences were significant.
1
52
THE EFFECTS OF CHANGING THE REFERENCE CATEGORY
However, suppose that we were interested in
testing whether the overhead costs of skilled
workers schools were different from those of the
other types of school. How could we do this? It
is possible to perform a t test using the
variance-covariance matrix of the regression
coefficients to calculate the relevant standard
errors. But it is a pain and it is easy to make
arithmetical errors.
3
53
THE EFFECTS OF CHANGING THE REFERENCE CATEGORY
It is much simpler to re-run the regression
making skilled workers schools the reference
category. Now we need to define a dummy variable
GEN for the general schools.
5
54
THE EFFECTS OF CHANGING THE REFERENCE CATEGORY
COST b1 dTTECH dVVOC dGGEN b2N
u
The model is shown in equation form. Note that
there is no longer a dummy variable for skilled
workers schools since they form the reference
category.
6
55
THE EFFECTS OF CHANGING THE REFERENCE CATEGORY
COST b1 dTTECH dVVOC dGGEN b2N
u Skilled Workers' School COST b1 b2N
u (TECH VOC GEN 0)
In the case of observations relating to skilled
workers schools, all the dummy variables are 0
and the model simplifies to the intercept and the
term involving N.
7
56
THE EFFECTS OF CHANGING THE REFERENCE CATEGORY
COST b1 dTTECH dVVOC dGGEN b2N
u Skilled Workers' School COST b1 b2N
u (TECH VOC GEN 0) Technical School COST
(b1 dT) b2N u (TECH 1 VOC GEN
0)
In the case of observations relating to technical
schools, TECH is equal to 1 and the intercept
increases by an amount dT.
8
57
THE EFFECTS OF CHANGING THE REFERENCE CATEGORY
COST b1 dTTECH dVVOC dGGEN b2N
u Skilled Workers' School COST b1 b2N
u (TECH VOC GEN 0) Technical School COST
(b1 dT) b2N u (TECH 1 VOC GEN
0)
Note that dT should now be interpreted as the
extra overhead cost of a technical school
relative to that of a skilled workers school.
9
58
THE EFFECTS OF CHANGING THE REFERENCE CATEGORY
COST b1 dTTECH dVVOC dGGEN b2N
u Skilled Workers' School COST b1 b2N
u (TECH VOC GEN 0) Technical School COST
(b1 dT) b2N u (TECH 1 VOC GEN
0) Vocational School COST (b1 dV) b2N
u (VOC 1 TECH GEN 0) General School COST
(b1 dG) b2N u (GEN 1 TECH VOC 0)
Similarly one can derive the implicit cost
functions for vocational and general schools,
their d coefficients also being interpreted as
their extra overhead costs relative to those of
skilled workers schools.
10
59
THE EFFECTS OF CHANGING THE REFERENCE CATEGORY
COST
Technical
dT
dG
b1dT
dV
b1
Workers
Vocational
b1dV
b1dG
General
N
This diagram illustrates the model graphically.
Note that the d shifts are measured from the line
for skilled workers schools.
11
60
THE EFFECTS OF CHANGING THE REFERENCE CATEGORY
. reg COST N TECH VOC GEN Source SS
df MS Number of obs
74 ---------------------------------------
F( 4, 69) 29.63 Model
9.2996e11 4 2.3249e11 Prob gt
F 0.0000 Residual 5.4138e11 69
7.8461e09 R-squared
0.6320 ---------------------------------------
Adj R-squared 0.6107 Total
1.4713e12 73 2.0155e10 Root
MSE 88578 ------------------------------
------------------------------------------------
COST Coef. Std. Err. t
Pgtt 95 Conf. Interval ----------------
--------------------------------------------------
----------- N 342.6335 40.2195
8.519 0.000 262.3978 422.8692 TECH
10748.51 30524.87 0.352 0.726
-50146.93 71643.95 VOC -90133.74
33984.22 -2.652 0.010 -157930.4
-22337.07 GEN -143362.4 27852.8
-5.147 0.000 -198927.2 -87797.57
_cons 88469.29 28849.56 3.067 0.003
30916.01 146022.6 ------------------------
--------------------------------------------------
----
Here is the Stata output for the regression. We
will focus first on the regression coefficients.
13
61
THE EFFECTS OF CHANGING THE REFERENCE CATEGORY
COST 88,000 11,000TECH - 90,000VOC -
143,000GEN 343N
The regression result is shown written as an
equation.
14
62
THE EFFECTS OF CHANGING THE REFERENCE CATEGORY
COST 88,000 11,000TECH - 90,000VOC -
143,000GEN 343N Skilled Workers' School COST
88,000 343N (TECH VOC GEN 0)
Putting all the dummy variables equal to 0, we
obtain the equation for the reference category,
the skilled workers schools.
15
63
THE EFFECTS OF CHANGING THE REFERENCE CATEGORY
COST 88,000 11,000TECH - 90,000VOC -
143,000GEN 343N Skilled Workers' School COST
88,000 343N (TECH VOC GEN 0) Technical
School COST 88,000 11,000 343N (TECH 1
VOC GEN 0) 99,000 343N
Putting TECH equal to 1 and VOC and GEN equal to
0, we obtain the equation for the technical
schools.
16
64
THE EFFECTS OF CHANGING THE REFERENCE CATEGORY
COST 88,000 11,000TECH - 90,000VOC -
143,000GEN 343N Skilled Workers' School COST
88,000 343N (TECH VOC GEN 0) Technical
School COST 88,000 11,000 343N (TECH 1
VOC GEN 0) 99,000 343N Vocational
School COST 88,000 - 90,000 343N (VOC 1
TECH GEN 0) -2,000 343N General
School COST 88,000 - 143,000 343N (GEN 1
TECH VOC 0) -55,000 343N
And similarly we obtain the equations for the
vocational and general schools, putting VOC and
GEN equal to 1 in turn.
17
65
THE EFFECTS OF CHANGING THE REFERENCE CATEGORY
COST 88,000 11,000TECH - 90,000VOC -
143,000GEN 343N Skilled Workers' School COST
88,000 343N (TECH VOC GEN 0) Technical
School COST 88,000 11,000 343N (TECH 1
VOC GEN 0) 99,000 343N Vocational
School COST 88,000 - 90,000 343N (VOC 1
TECH GEN 0) -2,000 343N General
School COST 88,000 - 143,000 343N (GEN 1
TECH VOC 0) -55,000 343N
Note that the cost functions turn out to be
exactly the same as when we used general schools
as the reference category.
18
66
THE EFFECTS OF CHANGING THE REFERENCE CATEGORY
Consequently the scatter diagram with regression
lines is exactly the same as before.
19
67
THE EFFECTS OF CHANGING THE REFERENCE CATEGORY
. reg COST N TECH VOC GEN Source SS
df MS Number of obs
74 ---------------------------------------
F( 4, 69) 29.63 Model
9.2996e11 4 2.3249e11 Prob gt
F 0.0000 Residual 5.4138e11 69
7.8461e09 R-squared
0.6320 ---------------------------------------
Adj R-squared 0.6107 Total
1.4713e12 73 2.0155e10 Root
MSE 88578 ------------------------------
------------------------------------------------
COST Coef. Std. Err. t
Pgtt 95 Conf. Interval ----------------
--------------------------------------------------
----------- N 342.6335 40.2195
8.519 0.000 262.3978 422.8692 TECH
10748.51 30524.87 0.352 0.726
-50146.93 71643.95 VOC -90133.74
33984.22 -2.652 0.010 -157930.4
-22337.07 GEN -143362.4 27852.8
-5.147 0.000 -198927.2 -87797.57
_cons 88469.29 28849.56 3.067 0.003
30916.01 146022.6 ------------------------
--------------------------------------------------
----
The goodness of fit, whether measured by R2, RSS,
or the standard error of the regression (the
estimate of the standard deviation of u, here
denoted Root MSE), is likewise not affected by
the change.
20
68
THE EFFECTS OF CHANGING THE REFERENCE CATEGORY
. reg COST N TECH VOC GEN Source SS
df MS Number of obs
74 ---------------------------------------
F( 4, 69) 29.63 Model
9.2996e11 4 2.3249e11 Prob gt
F 0.0000 Residual 5.4138e11 69
7.8461e09 R-squared
0.6320 ---------------------------------------
Adj R-squared 0.6107 Total
1.4713e12 73 2.0155e10 Root
MSE 88578 ------------------------------
------------------------------------------------
COST Coef. Std. Err. t
Pgtt 95 Conf. Interval ----------------
--------------------------------------------------
----------- N 342.6335 40.2195
8.519 0.000 262.3978 422.8692 TECH
10748.51 30524.87 0.352 0.726
-50146.93 71643.95 VOC -90133.74
33984.22 -2.652 0.010 -157930.4
-22337.07 GEN -143362.4 27852.8
-5.147 0.000 -198927.2 -87797.57
_cons 88469.29 28849.56 3.067 0.003
30916.01 146022.6 ------------------------
--------------------------------------------------
----
But the t tests are affected. In particular, the
meaning of a null hypothesis for a dummy variable
coefficient being equal to 0 is different.
21
69
THE EFFECTS OF CHANGING THE REFERENCE CATEGORY
. reg COST N TECH VOC GEN Source SS
df MS Number of obs
74 ---------------------------------------
F( 4, 69) 29.63 Model
9.2996e11 4 2.3249e11 Prob gt
F 0.0000 Residual 5.4138e11 69
7.8461e09 R-squared
0.6320 ---------------------------------------
Adj R-squared 0.6107 Total
1.4713e12 73 2.0155e10 Root
MSE 88578 ------------------------------
------------------------------------------------
COST Coef. Std. Err. t
Pgtt 95 Conf. Interval ----------------
--------------------------------------------------
----------- N 342.6335 40.2195
8.519 0.000 262.3978 422.8692 TECH
10748.51 30524.87 0.352 0.726
-50146.93 71643.95 VOC -90133.74
33984.22 -2.652 0.010 -157930.4
-22337.07 GEN -143362.4 27852.8
-5.147 0.000 -198927.2 -87797.57
_cons 88469.29 28849.56 3.067 0.003
30916.01 146022.6 ------------------------
--------------------------------------------------
----
For example, the t statistic for the technical
school coefficient is for the null hypothesis
that the overhead costs of technical schools are
the same as those of skilled workers schools.
22
70
THE EFFECTS OF CHANGING THE REFERENCE CATEGORY
. reg COST N TECH VOC GEN Source SS
df MS Number of obs
74 ---------------------------------------
F( 4, 69) 29.63 Model
9.2996e11 4 2.3249e11 Prob gt
F 0.0000 Residual 5.4138e11 69
7.8461e09 R-squared
0.6320 ---------------------------------------
Adj R-squared 0.6107 Total
1.4713e12 73 2.0155e10 Root
MSE 88578 ------------------------------
------------------------------------------------
COST Coef. Std. Err. t
Pgtt 95 Conf. Interval ----------------
--------------------------------------------------
----------- N 342.6335 40.2195
8.519 0.000 262.3978 422.8692 TECH
10748.51 30524.87 0.352 0.726
-50146.93 71643.95 VOC -90133.74
33984.22 -2.652 0.010 -157930.4
-22337.07 GEN -143362.4 27852.8
-5.147 0.000 -198927.2 -87797.57
_cons 88469.29 28849.56 3.067 0.003
30916.01 146022.6 ------------------------
--------------------------------------------------
----
The t ratio in question is only 0.35, so the null
hypothesis is not rejected.
23
71
THE EFFECTS OF CHANGING THE REFERENCE CATEGORY
. reg COST N TECH VOC GEN Source SS
df MS Number of obs
74 ---------------------------------------
F( 4, 69) 29.63 Model
9.2996e11 4 2.3249e11 Prob gt
F 0.0000 Residual 5.4138e11 69
7.8461e09 R-squared
0.6320 ---------------------------------------
Adj R-squared 0.6107 Total
1.4713e12 73 2.0155e10 Root
MSE 88578 ------------------------------
------------------------------------------------
COST Coef. Std. Err. t
Pgtt 95 Conf. Interval ----------------
--------------------------------------------------
----------- N 342.6335 40.2195
8.519 0.000 262.3978 422.8692 TECH
10748.51 30524.87 0.352 0.726
-50146.93 71643.95 VOC -90133.74
33984.22 -2.652 0.010 -157930.4
-22337.07 GEN -143362.4 27852.8
-5.147 0.000 -198927.2 -87797.57
_cons 88469.29 28849.56 3.067 0.003
30916.01 146022.6 ------------------------
--------------------------------------------------
----
The t ratio for the coefficient of VOC is -2.65,
so one concludes that the overheads of vocational
schools are significantly lower than those of
skilled workers schools, at the 1 significance
level.
24
72
THE EFFECTS OF CHANGING THE REFERENCE CATEGORY
. reg COST N TECH VOC GEN Source SS
df MS Number of obs
74 ---------------------------------------
F( 4, 69) 29.63 Model
9.2996e11 4 2.3249e11 Prob gt
F 0.0000 Residual 5.4138e11 69
7.8461e09 R-squared
0.6320 ---------------------------------------
Adj R-squared 0.6107 Total
1.4713e12 73 2.0155e10 Root
MSE 88578 ------------------------------
------------------------------------------------
COST Coef. Std. Err. t
Pgtt 95 Conf. Interval ----------------
--------------------------------------------------
----------- N 342.6335 40.2195
8.519 0.000 262.3978 422.8692 TECH
10748.51 30524.87 0.352 0.726
-50146.93 71643.95 VOC -90133.74
33984.22 -2.652 0.010 -157930.4
-22337.07 GEN -143362.4 27852.8
-5.147 0.000 -198927.2 -87797.57
_cons 88469.29 28849.56 3.067 0.003
30916.01 146022.6 ------------------------
--------------------------------------------------
----
General schools clearly have lower overhead costs
than the skilled workers schools, according to
the regression.
25
73
THE EFFECTS OF CHANGING THE REFERENCE CATEGORY
. reg COST N TECH WORKER VOC --------------------
--------------------------------------------------
-------- COST Coef. Std. Err.
t Pgtt 95 Conf. Interval ----------
--------------------------------------------------
----------------- N 342.6335
40.2195 8.519 0.000 262.3978
422.8692 TECH 154110.9 26760.41
5.759 0.000 100725.3 207496.4 WORKER
143362.4 27852.8 5.147 0.000
87797.57 198927.2 VOC 53228.64
31061.65 1.714 0.091 -8737.646
115194.9 _cons -54893.09 26673.08
-2.058 0.043 -108104.4
-1681.748 ----------------------------------------
-------------------------------------- . reg COST
N TECH VOC GEN -----------------------------------
-------------------------------------------
COST Coef. Std. Err. t Pgtt
95 Conf. Interval ------------------------
--------------------------------------------------
--- N 342.6335 40.2195 8.519
0.000 262.3978 422.8692 TECH
10748.51 30524.87 0.352 0.726
-50146.93 71643.95 VOC -90133.74
33984.22 -2.652 0.010 -157930.4
-22337.07 GEN -143362.4 27852.8
-5.147 0.000 -198927.2 -87797.57
_cons 88469.29 28849.56 3.067 0.003
30916.01 146022.6 ------------------------
--------------------------------------------------
----
Note that there are some differences in the
standard errors. The standard error of the
coefficient of N is unaffected.
26
74
THE EFFECTS OF CHANGING THE REFERENCE CATEGORY
. reg COST N TECH WORKER VOC --------------------
--------------------------------------------------
-------- COST Coef. Std. Err.
t Pgtt 95 Conf. Interval ----------
--------------------------------------------------
----------------- N 342.6335
40.2195 8.519 0.000 262.3978
422.8692 TECH 154110.9 26760.41
5.759 0.000 100725.3 207496.4 WORKER
143362.4 27852.8 5.147 0.000
87797.57 198927.2 VOC 53228.64
31061.65 1.714 0.091 -8737.646
115194.9 _cons -54893.09 26673.08
-2.058 0.043 -108104.4
-1681.748 ----------------------------------------
-------------------------------------- . reg COST
N TECH VOC GEN -----------------------------------
-------------------------------------------
COST Coef. Std. Err. t Pgtt
95 Conf. Interval ------------------------
--------------------------------------------------
--- N 342.6335 40.2195 8.519
0.000 262.3978 422.8692 TECH
10748.51 30524.87 0.352 0.726
-50146.93 71643.95 VOC -90133.74
33984.22 -2.652 0.010 -157930.4
-22337.07 GEN -143362.4 27852.8
-5.147 0.000 -198927.2 -87797.57
_cons 88469.29 28849.56 3.067 0.003
30916.01 146022.6 ------------------------
--------------------------------------------------
----
The one test involving the dummy variables that
can be performed with either specification is the
test of whether the overhead costs of general
schools and skilled workers schools are
different. The choice of specification can make
no difference to the outcome of this test. The
only difference is caused by the fact that the
regression coefficient has become negative in the
second specification. The standard error is the
same, so the t statistic has the same absolute
magnitude and the outcome of the test must be the
same.
27
75
THE EFFECTS OF CHANGING THE REFERENCE CATEGORY
. reg COST N T