Kein Folientitel

1
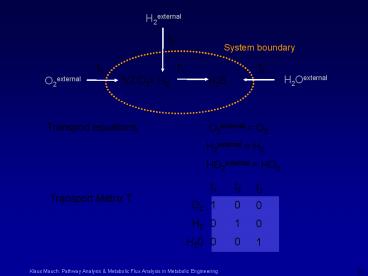
Transport equations
O2external O2 H2external H2 HO2external HO2
t1 1 0 0
O2 H2 H20
t2 0 1 0
t3 0 0 1
Transport Matrix T
2
(No Transcript)
3
(No Transcript)
4
Elemental Balance
In biosystems, elements (C, H, N, O, P, S) are
always conserved, thus
O 2 0 1
O2 H2 H20
H 0 2 2
Elemental Composition Matrix E
5
Reaction equation 1/2 O2 H2 H2O
6
BRENDA Threonine dehydratase
7
Reaction equation L-Homoserine PyruvateNH3
C4 H9 N O3 C3 H4 O3 NH3
8
Elemental Balances May Reveal Inconsistencies in
Biochemical Reaction Systems
Should read L-Homoserine 2-Oxobutyrate NH3
9
(No Transcript)
10
Pathway (Topological) Analysis Metabolic Flux
Analysis
11
Metabolic Network - Regulatory NetworkHierarchica
l Organisation
Metabolic Network
12
Pathway Analysis Flux Analysis
Metabolic Network
13
Introduction Pathway AnalysisMetabolic Flux
AnalysisExample

• Bioinformatics and Metabolic Engineering
• Structured metabolic models
• Metabolite balancing
• Conserved moieties
• Elementary flux modes
• Estimation of flux distributions
• Observability of metabolic fluxes
• Overdetermined and underdetermined systems
• Metabolic model of Saccharomyces cerevisiae
• Model Analysis

14
Chemical entities (atoms, ions, assemblies of
atoms or ions) participating in a reaction system
without loss of integrity and always remaining in
the system (even if it is an open one) are called
conserved moieties. Example of a conservation
relation NADH NAD const.
15
r1 Acetaldehyde H2ONAD AcetateNADH2 H r2
1/2 O2 NADHH H2O NAD
16
r1 -1 1 0 -1 -1 1 -1
r2 0 0 -1/2 1 2 -1 1
t1 1 0 0 0 0 0 0
t2 0 1 0 0 0 0 0
t3 0 0 1 0 0 0 0
t4 0 0 0 1 0 0 0
Acetaldehyde Acetate O2 H20 H NADH NAD
t5 0 0 0 0 1 0 0
NADH NAD const.
17
The presence of conservation relations leads to
linear dependent rows in the balance matrix N.
18
r1 -1 1 0 -1 -1 1 -1
r2 0 0 -1/2 1 2 -1 1
t1 1 0 0 0 0 0 0
t2 0 1 0 0 0 0 0
t3 0 0 1 0 0 0 0
t4 0 0 0 1 0 0 0
Acetaldehyde Acetate O2 H20 H NADH NAD
t5 0 0 0 0 1 0 0
N0
N
19
(No Transcript)
20
(No Transcript)
21
Since a metabolic reaction network comprises n
conservation relations (conserved moieties), n
algebraic relations between the balanced
metabolites occur.
22
Introduction Pathway AnalysisMetabolic Flux
AnalysisExample

• Bioinformatics and Metabolic Engineering
• Structured metabolic models
• Metabolite balancing
• Conserved moieties
• Elementary flux modes
• Estimation of flux distributions
• Observability of metabolic fluxes
• Overdetermined and underdetermined systems
• Metabolic model of Saccharomyces cerevisiae
• Model Analysis

23
Null- Space (Kernel)
N v 0
24
-1/2 -1 1
1 0 0
0 1 0
0 0 1
O2 H2 H2O
-1/2 -1 1
1 0 0
0 1 0
0 0 1
O2 H2 H2O
r1 t1 t2 t3
0 0 0

25
-1/2 -1 1
1 0 0
0 1 0
0 0 1
1 0 0
0 1 0
0 0 1
1 1/2 1
O2 H2 H2O
r1 t1 t2 t3
0 0 0

Row reduced echelon form of matrix N
26
1
1/2
1
1
-1/2 -1 1
1 0 0
0 1 0
0 0 1
1 0 0
0 1 0
0 0 1
1 1/2 1
O2 H2 H2O
1 1/2 1 -1
0 0 0

27
1
1
1/2
1
-1/2 -1 1
1 0 0
0 1 0
0 0 1
1 0 0
0 1 0
0 0 1
1 1/2 1
O2 H2 H2O
-1 -1/2 -1 1
0 0 0

28
The basis of the kernel of N does NOT
necessarily fulfil reversibility properties.
29
Degrees of Freedom
Degrees of Freedom number of fluxes - number of
linear independent rows of balance matrix N
Degrees of Freedom number of fluxes - rank(N)
Degrees of Freedom dim(kernel(N))
30
-1/2 -1 1
1 0 0
0 1 0
0 0 1
O2 H2 H2O
-1/2 -1 1
1 0 0
0 1 0
0 0 1
O2 H2 H2O
r1 t1 t2 t3
0 0 0

Degree of Freedom 4-31
31
r1 -1 1 0 -1 -1 1 -1
r2 0 0 -1/2 1 2 -1 1
t1 1 0 0 0 0 0 0
t2 0 1 0 0 0 0 0
t3 0 0 1 0 0 0 0
t4 0 0 0 1 0 0 0
Acetaldehyde Acetate O2 H20 H NADH NAD
t5 0 0 0 0 1 0 0
Degree of Freedom 7-6 1
32
v1 v2 v3
v1 1
v2 -1
v3 -1
M
0

irreversible
Degrees of Freedom number of fluxes -
rank(N) Degrees of Freedom 3 -1 2 The
Null-Space (kernel) is spanned by 2 base vectors
(flux modes)
33
a) Flux vectors spanning the kernel of N
1
1
1
0
0
1
Flux Mode 1 a)
Flux Mode 2 a)
34
b) Flux vectors spanning the kernel of N
2
1
1
0
1
1
Flux Mode 1 b)
Flux Mode 2 b)
35
The base of the kernel of N is NOT unique.
36
Flux Mode 1 b)
37
Elementary Flux Modes

• Fulfil steady state condition
• Fulfil reversibilty properties
• Can not be decomposed into smaller modes (i.e.
  modes that involve less enzymes)

38
Network Design
39
GLUCOSE
RIBU5P
G6P
ATP
XYL5P
RIB5P
F6P
NADP
E4P
F6P
GAP
ADP
3PG
NADPH
Pi
PEP
CO2
PYR
ACCOA
H2O
COA
THREONIN
OAC
ISOCIT
NAD
H
MAL
FADH2
AKG
FAD
NADH
FUM
SUC
40
(No Transcript)
41
irreversible
42
Elementary Flux Mode 1
Y THREONIN / GLUCOSE 4/3
43
Elementary Flux Mode 2
Y THREONIN / GLUCOSE 1
44
Elementary Flux Mode 3
Y THREONIN / GLUCOSE 2/3
45
Elementary Flux Mode 4
Y THREONIN / GLUCOSE 0
46
1
Elementary Flux Mode 5
GLUCOSE
3
RIBU5P
G6P
2
Y THREONIN / GLUCOSE 0
XYL5P
RIB5P
F6P
E4P
F6P
GAP
1
3PG
PEP
PYR
ACCOA
1
OAC
ISOCIT
MAL
AKG
FUM
SUC
47
1
Elementary Flux Mode 6
GLUCOSE
G6P
Y THREONIN / GLUCOSE 0
F6P
GAP
2
3PG
PEP
PYR
ACCOA
2
OAC
ISOCIT
MAL
AKG
FUM
SUC
48
RIBU5P
G6P
6PG
XYL5P
RIB5P
F6P
E4P
F6P
GAP
2PG
FALD
METOH
PEP
PYR
ACCOA
THREONIN
OAC
ISOCIT
GLYO
MAL
AKG
FUM
SUC
49
(No Transcript)
50
(No Transcript)
51
(No Transcript)
52
Elementary Flux Modes
Use in Metabolic Engineering

• Optimal and suboptimal yields can be easily
  obtained
• Identification of dispensable enzymes (bypass)
• Medium optimisation

53
Elementary Flux Modes
Use in Modelling Tools

• Identification of the complete material flow
  functioning
• Identification of parts of the network without
  any function (dead subnets)
• Identification of futile cycles

54
Elementary Flux Modes
Some Properties

• The set of elementary flux modes is unique
• The vector space spanned by elementary flux modes
  exceeds (or equals) the dimension of the kernel

55
Introduction Pathway AnalysisMetabolic Flux
AnalysisExample

• Bioinformatics and Metabolic Engineering
• Structured metabolic models
• Metabolite balancing
• Conserved moieties
• Elementary flux modes
• Estimation of flux distributions
• Observability of metabolic fluxes
• Overdetermined and underdetermined systems
• Metabolic model of Saccharomyces cerevisiae
• Model Analysis

56
Estimation of Metabolic Fluxes
57
Experimental Determination ofNet Conversion Rates
58
Estimation of Metabolic Fluxes
59
Estimation of Metabolic Fluxes
60
Estimation of Metabolic Fluxes
A) Exactly Determined System
B) Overdetermined System
C) Underdetermined System
61
Estimation of Metabolic Fluxes
Exactly Determined System without conservation
relations
Observability criterion
62
Estimation of Metabolic Fluxes
Underdetermined System
An underdetermined system can never be observed
63
Estimation of Metabolic Fluxes
Overdetermined System
Observability criterion
64
An overdetermined system isNOT always observable.
65
v2
v1
v4
v5
S0
S1
M1
M2
M3
v3
Degrees of freedom 2
66
v2
v1
v4
v5
S0
S1
M1
M2
M3
v3
Degrees of freedom 2
Fluxes derived from measurements v1, v4, v5
Not observeable v2, v3
67
v2
v1
v4
v5
Vnetv3-v2
S0
S1
M1
M2
M3
v3
Degrees of freedom 2
Fluxes derived from measurements v1, v4, v5
Observeable vnet v3 -v2
68
v2
v1
v4
v5
S0
S1
M1
M2
M3
v3
Degrees of freedom 2
Derived from measurements v1, v3, v5
Observeable v2, v4
69
Model Validation
Invalid Model / Inconsistent Data
70
c2 -Distribution
71
Introduction Pathway AnalysisMetabolic Flux
AnalysisExample

• Bioinformatics and Metabolic Engineering
• Structured metabolic models
• Metabolite balancing
• Conserved moieties
• Elementary flux modes
• Estimation of flux distributions
• Observability of metabolic fluxes
• Overdetermined and underdetermined systems
• Metabolic model of Saccharomyces cerevisiae
• Model Analysis

72
Metabolic Model of Saccharomyces cerevisiae
73
Nutrients
Excreted Products
Biomass
74
Macromolecular Composition of Saccharomyces
cerevisiae
75
Model Structure
GlucoseAcetateCO2O2EthanolGlycerolHH2OAmm
oniaSulphatePhosphateBiomass
GlycolysisPentose Phosphate PathwayAnabolismSyn
thesis of Macromolecules (Polymerisation)
Cytosol
System boundary
76
Introduction Pathway AnalysisMetabolic Flux
AnalysisExample

• Bioinformatics and Metabolic Engineering
• Structured metabolic models
• Metabolite balancing
• Conserved moieties
• Elementary flux modes
• Estimation of flux distributions
• Observability of metabolic fluxes
• Overdetermined and underdetermined systems
• Metabolic model of Saccharomyces cerevisiae
• Model Analysis

77
Conservation Relations
nadcytnadhcyt const nadmitnadhmit
const. nadpcytnadphcyt const. accoAcytaccoAmit
coAcytcoAmitsuccoAcytsuccoAmit
const. fadmitfadh2mit const. fthfcytmethfcyt
mythfcytthfcyt const.
78
Violated Conservation Relation
79
Yields of Amino Acids on Glucose Obtained from
Elementary Flux Modes
80
Maximal Theoretical Yields ofAmino Acids on
Glucose
81
Maximal Yields ofMacromolecules on Glucose
82
Maximal Yield ofBiomass on Glucose
1 composition of macromolecules taken at a growth
rate of m 0.1 h-1 2 same metabolic network but
without compartmentation
83
Medium Design Effect of Additives on the Yield
of Biomass on Glucose
D Y (g/g)
84
Net Conversion Rates
85
Saccharomyces cerevisia CBS 7336 D0.10 h-1
Cytosol
Mitochondrien
86
Saccharomyces cerevisia CBS 7336 D0.33 h-1
87
Index
Bioinformatics and Metabolic Engineering
Structured metabolic models Metabolite
balancing Conserved moieties Elementary flux
modes Estimation of flux distributions
Observability of metabolic fluxes Overdetermined
and undertetermined systems Metabolic model of
Saccharomyces cerevisiae Model Analysis
Computational Aspects