Silicon - PowerPoint PPT Presentation
1 / 15
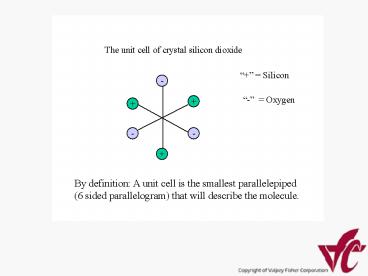
Title: Silicon
1
Silicon
- Oxygen
By definition A unit cell is the smallest
parallelepiped (6 sided parallelogram) that will
describe the molecule.
2
Unit Cell Under Mechanical Compression
(pushing force) Electrical polarity as shown
Unit Cell at Rest
- - -
- - -
Neutral Charge
Unit Cell Under mechanical Tension (pulling
force) Electrical polarity reverses.
3
2 compression forces in opposite directions...
Unit Cell at Rest
- - -
Neutral Charge
Will also result in electrical energy!
This is called a shear force, and is the most
common mechanical distortion in crystals we
make This is where the famous term Thickness
Shear has its origins.-AT, -BT, SC crystals
all are shear mode devices (more on this later)
4
What we have learned so far .
- The unique piezoelectric and converse
piezoelectric properties of crystalline quartz
allow us to design an electro-mechanical device
(mechanical force electrical signal electrical
field mechanical deformation) - By operating the device at its mechanical
resonance frequency, we can get a useful
electrical signal out of it The electrical
signal will be at the same frequency as the
mechanical resonance frequency. - If we know how to control the devices mechanical
resonance frequency, we ought to be able to
design a device at any frequency of interest..
5
Definition of Frequency.
- For purposes of this class, the term frequency
refers to a mathematical description of a
periodic (or repeating) signal. - Since all of the devices we build at VF are
designed to produce a very stable frequency
signal, we can analyze a typical output signal to
get a general feeling how the signal behaves.
6
Anatomy of a Sine Wave and a Square Wave
Sine Wave
Square Wave
7
Amplitude, pk to pk
Time
Wavelength
Period
Amplitude A measure of how big the signal is.
Usually expressed in
Electrical Units (voltage or current). Wavelength
How long the signal is (usually in
meters). Period How much time it takes
to complete 1 cycle (measured in
seconds). Frequency The number of complete
cycles in a 1 second chunk of time.
Frequency is equivalent to 1/Period, and
is commonly measured in
Hertz 1 Hz 1 cycle per second
8
Now, we should have enough information to allow
us to design a crystal. We will build an y-cut
extensional vibrational mode crystal that will
operate at a fundamental resonance frequency of
50 kHz...
Same crystal with driving signal applied,
operating in length extension mode.
Electrode
Crystal at rest
Wires for circuit attachment
Extensional Mode is the 5.00 term meaning the
part gets longer when an electrical field is
applied (remember E field mechanical
deformation!). We also need a pair of
electrodes to connect to a circuit These are
simply a couple of conductive plates attached to
the major faces of the crystal.
9
First, you need to know how to reference the
crystal out of the raw crystal stone. Both X-cut
and Y-cut crystals are simply cut parallel to
their respective axes (more complicated cuts
require x-ray technology to locate the crystal
axis orientation)
z
x
y
10
For the case of an X-cut or Y-cut, the resonance
frequency is related to the geometry of the
blank by a 1/2 wavelength ratio. This is similar
in nature to the xylophone, where each metal bar
is tuned to an audible tone.
I offer the following mathematical relationship
without proof so as to avoid confusion. I have
provided this proof in the class notes I sent
out to everyone. For now, just take my word for
it...
fx is the frequency in the x direction. n is
the harmonic order (dont worry about
this for now). t is the thickness of the
crystal. kx is known as the frequency
constant in the x direction.
fy is the frequency in the y direction. n is
the harmonic order (dont worry about
this for now). l is the length of the
crystal. ky is known as the frequency
constant in the y direction.
11
fx We want 50 kHz. n 1, for fundamental
mode. l is the thickness of the crystal. ky
In the Y direction, this is 2600 kHz-mm
PROBLEM 1 fx We dont want the crystal to
vibrate in the x (thickness) direction at all!
This may cause interference with the vibration in
the x direction. Also, the frequency constant
is different in the x direction (2870 kHz-mm)
This is due to the anisotropic nature of quartz
That is, due to the crystalline molecular
structure, some physical properties of the device
change with direction.
12
One clever way around this dilemma is to change
the aspect ratio so that the dominant resonance
is in the direction of interest. Aspect ratio
is engineer-ese for the length-to-thickness
ratio, in this case. EXAMPLE For an aspect ratio
of 101, a 10 mm length has a 1 mm thickness.
Lets take a guess and make the length 10 times
the width And begin the design
13
This is about 2 inches, so with an aspect
ratio of 101, the thickness will be 5.2 mm, or
about 0.2
14
Since we have not put any restrictions on the Z
axis (which is the width), we can choose to go
with a convenient value that will take other
design aspects into account. Lets say that the
only electrodes available to us are 0.35
0.35 9 mm. Now, we can simply make the Z
width something slightly larger. Lets try a
length to width aspect ratio of 5 (eg length is
5 times the width).
This width should work fine for our 9 mm
electrode.
15
Summary of the finished design
Length 52.0 mm (2.05) Width
10.4 mm (0.41) Thickness 5.2 mm
(0.20) Electrode W. 9.0 mm (0.35)
Elec.
l
t
w