Folie 1 - PowerPoint PPT Presentation
1 / 8
Title:
Folie 1
Description:
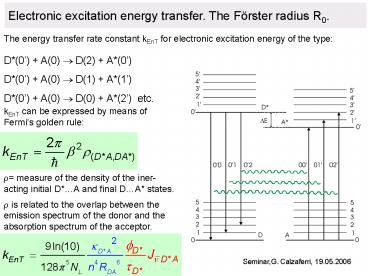
The energy transfer rate constant kEnT for electronic ... kEnT can be expressed by means of Fermi's golden rule: r is related to the overlap between the ... – PowerPoint PPT presentation
Number of Views:41
Avg rating:3.0/5.0
Title: Folie 1
1
Electronic excitation energy transfer. The
Förster radius R0.
The energy transfer rate constant kEnT for
electronic excitation energy of the type
D(0) A(0) D(2) A(0)
D(0) A(0) D(1) A(1)
D(0) A(0) D(0) A(2) etc.
kEnT can be expressed by means of Fermis golden
rule
- measure of the density of the iner-acting
initial DA and final DA states.
- r is related to the overlap between the
- emission spectrum of the donor and the
- absorption spectrum of the acceptor.
2
The formula is correct if the dimension of J
is chosen to be cm6mol-1
For chemists the more natural way to choose
the dimension of the spectral overlap integral
is J cm3M-1, M mol L-1.
3
Förster energy transfer radius R0
Luminescence rate of D
Energy transfer rate
At a specific D.A distance, the rate at which
D emits light is equal to the rate at which it
transfers its excitation energy A. At this
distance R0 we can write
Inserting kEnT
From this we find the Förster radius R0 for
electronic excitation energy transfer.
4
Förster radius R0 for electronic excitation
energy transfer
R0 is equal to the donor- acceptor distance at
which the probability for energy transfer is
equal to 0.5.
Distance dependence of the energy transfer rate
constant
5
K. Lutkouskaya, G. Calzaferri J. Phys. Chem. B
2006, 110, 5633
6
Luminescence rate of D
Energy transfer rate
The probability P for energy transfer is
cancelling
FRET
7
3D a 6 2D a 4, 1D a 2
8
One-dimensional electronic excitation energy
migration
0.13 ns
9
0.27 ns
0.45 ns
11
0.89 ns
16
23
C. Minkowski, G. Calzaferri, Angew. Chem. 2005,
44, 5325