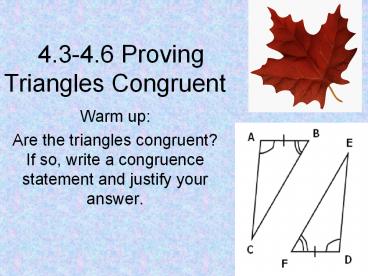
4.3-4.6 Proving Triangles Congruent

1
4.3-4.6 Proving Triangles Congruent

• Warm up
• Are the triangles congruent? If so, write a
  congruence statement and justify your answer.

2
Proving Triangles Congruent

• How can you prove sides congruent? (things to
  look for)
• How can you prove angles congruent?

Given Shared side(reflexive POE) Midpoints Segm
ent Addition Property Segment bisector Transitiv
e POE others?
Given Shared angle(reflexive POE) //?Alt. Int
lts, . . . Angle Addition Property Angle
bisector Vertical Angles Right
Angles(-) Transitive POE
3
Now you try!
N

• GIVEN
• ?R ? ?M
• MN RS
• MO RT
• PROVE
• ?MNO ? ?RST

O
M
S
R
T
what is the first step?
4
Now you try!
N

• GIVEN
• ?R ? ?M
• MN RS
• MO RT
• PROVE
• ?MNO ? ?RST

O
M
S
R
T
STEP 1 DRAW IT AND MARK IT!
5
Now you try!
N

• GIVEN
• ?R ? ?M
• MN RS
• MO RT
• PROVE
• ?MNO ? ?RST

O
M
S
R
T
STEP 1 DRAW IT AND MARK IT! STEP 2 CAN YOU
PROVE THE ?s ? HOW?
6
Now you try!
N

• GIVEN
• ?R ? ?M
• MN RS
• MO RT
• PROVE
• ?MNO ? ?RST

O
M
S
R
T
YES, BY SAS FROM THE GIVENS!
7
REAL LIFE EXAMPLES
Bridges Golden Gate, Brooklyn Bridge, New
River Bridge . . . .
8
Real Life
9
Real Life
10
Types of Proofs

• Traditional two-column This looks like a
  T-chart and has the statements on the left and
  reasons on the right.

11
Types of Proofs
Flow Chart Starts from a base line and all
information flows from the given. Great for
visual learners. Paragraph Write it out!
Tell me what youre doing!
12
Helpful Hints with Proofs

• ALWAYS mark the given in your picture.
• Use different colors in your picture to see the
  parts better.
• ALWAYS look for a _______________________ which
• uses the __________________ property.
• ALWAYS look for ______________ lines to prove
  mostly
• that _____________________________________
  .
• ALWAYS look for ____________ angles which are
  always
• ___________.

common side/angle
reflexive
parallel
alternate interior angles are congruent
vertical
congruent
13
Given PQ ? PS QR ? SR ?1 ? ?2 Prove ? 3 ? ?
4

• Statements
• PQ ? PS QR ? SR
• ?1 ? ?2
• PR ? PR
• ?QPR ? ?SPR
• ?3 ? ?4

• Reasons
• Given
• Reflexive Property
• SAS Postulate
• CPCTC

14
Given WO ? ZO XO ? YOProve ?WXO ? ?ZYO

• Statements
• WO ? ZO XO ? YO
• ?WOX ? ?ZOY
• ?WXO ? ?ZYO

• Reasons
• Given
• Vertical angles are ?.
• SAS Postulate

15
Proof Practice

• Given ?PSU ? ?PTR SU ? TR
• Prove SP ? TP
• HINT draw the triangles separately!

16
Proof Practice
1. ?PSU ? ?PTR SU ? TR
1. given
2. ltP ? ltP
2. Reflexive POE
3. ?SUP ? ?TRP
3. AAS Theorem
4. CPCTC
4. SP ? TP
17
Proof Practice
?PSU ? ?PTR
ltP ? ltP
SU ? TR
AAS Theorem
?SUP ? ?TRP
CPCTC
SP ? TP
18
Practice

• Name the included side for ?1 and ?5.
• Name a pair of angles in which DE is not
  included.
• If ?6 ? ?10, and DC ? VC, then
• ? DCA ? ? _______, by _________.

DC
lt8, lt9, for example
VCE
ASA
19
More ProofsUsing 2 Column

• Given PQ ? RQ S is midpoint of PR.
• Prove ?P ? ?R
• QS is an auxiliary line

1. PQ ? RQ S is midpoint of PR
1. given
2. PS ? SR
2. Def midpoint
3. QS ? QS
3. Reflexive POE
4. ?PQS ? ?RQS
4. SSS Postulate
5. ?P ? ?R
5. CPCTC
20
More ProofsUsing Flow Chart

• Given PQ ? RQ
• S is midpoint of PR.
• Prove ?P ? ?R

PQ ? RQ
S is midpoint of PR
QS ? QS
PS ? SR
SSS Postulate
?PQS ? ?RQS
CPCTC
?P ? ?R
21
More ProofsUsing Paragraph

• Given PQ ? RQ S is midpoint of PR.
• Prove ?P ? ?R
• QS is an __________________.
• We are given that ____________ and
  ___________________. Because
• S is the midpoint, we know that
  __________because of _____________.
• We drew in QS so that we can use the reflexive
  property to prove that
• _________. We now have enough information to
  prove that ?PQS ? ?RQS
• by ____________. Therefore ltP ? ltR by
  __________________.

auxiliary line
PQ ? RQ
S is midpoint of PR
def. of midpt
PS ? SR
QS ? QS
SSS Post.
CPCTC
22
Do the following proofs in whatever way you feel
comfortable

• Given AB ? EB ?DEC ? ?B
• Prove ?ABE is equilateral

23
Group Work Time

• Group 4.3-4.6 proof practice WS
• Group presentations

• Next Class
• Group presentations
• More group practice work