XRD XRay Diffraction

1
XRD X-Ray Diffraction
2
X-rays

• Another part of the electromagnetic spectrum
  between 100 and 0.2 Å.
• Plancks law Ehn hc/l
• Where n is frequency, l is wavelength, h is
  Plancks constant, and c is the speed of light

3
X-ray generation

• X-rays are generated by striking a target
  material with an accelerated e- which causes an
  excitation. When his excitation relaxes, or
  goes back down to standard state, an X-ray is
  emitted
• Usually given in terms of the energy levels those
  e- come from and go to ? different levels yield
  X-rays of different energies (all dependent on
  the material)
• K, L, M shells of a material, from that those
  shells have different transitions and
  characteristic relaxations (a, b, g)
• Cu Ka is the most intense peak and most commonly
  used (though others are possible and have a
  different wavelength, which can be useful!)

4
X-Ray interaction

• Scattering oscillation of incoming X-rays
  transfer energy to electrons in material,
  emitting secondary radiation at about the same
  frequency and energy as the incoming beam
• Interaction of X-rays with same material causes
  some electrons to go into an excited state, which
  upon relaxation, emits radiation characteristic
  of the atom it excited ? basis for XRF, used to
  identify chemical makeup of materials
• As with other interactions with minerals, there
  can also be reflection and transmission of X-rays
  (depending on thickness), but we dont typically
  use that information.

5
Interference

• Constructive and destructive interference wave
  properties interact to either cancel out or
  amplify each other.
• When 2 centers are emitting energy at some
  wavelength, they will interfere with each other

Plane view
6
Experiment

• Relationship between light as particles vs. light
  as waves
• Light scattered by mesh - as it travels and
  interacts, some waves compliment each other while
  different waves cancel each other

7
Diffraction

• Combine elements of interference with striking
  the x-ray at an angle to the material
• Relationship between wavelength, atomic spacing,
  and angle of diffraction for 3-D structures
  derived by von Laue
• Braggs determined that you could simplify this
  and treat it as a reflection off of the planes
  within an atom

8
Braggs Law

• nl2dsinT
• Where n is the order of diffraction (always an
  integer), l is the wavelength of incident
  radiation, d is the spacing between planes, and T
  is the angle of incidence (or angle of
  reflection, they are equal)

9
Diffraction

• Relationship between diffraction and wavelength
• The smaller the diffracting object, the greater
  the angular spacing of the diffraction pattern
• i.e. the smaller the separation between planes,
  the wider the spacing between diffraction lines
• What then is diffraction??
• The failure of light to travel in straight lines
  (much to Newtons dismay)
• Youngs 2 slit experiment proved light could bend
  scattered and affected by constructive and
  destructive interference
• Bright red constructive dark destructive

10
Braggs Law

• nl2dsinT
• Where n is the order of diffraction (always an
  integer), l is the wavelength of incident
  radiation, d is the spacing between planes, and T
  is the angle of incidence (or angle of
  reflection, they are equal)
• Diffraction here is between parallel planes of
  atoms ? the space between them (d) determines the
  angle of diffraction.
• Looking at the laser pattern again ? where is
  Braggs Law satisfied and how many orders of
  diffraction do we see?

11
Red Laser analogue

• We see orders of diffraction resulting from light
  coming between grid spacing 2, 3, 4, 5, etc.,
  apart. In a mineral, multiple parallel planes
  yields similar patterns at higher orders of
  diffraction theoretically the angle keeps
  increasing ? what do we notice about the
  intensity though?

12
Braggs Law

• nl2dsinT
• Just needs some satisfaction!!

13
X-Ray Diffraction (XRD) equipment
XRD machines vary angle as 2T because that angle
is always relative to incident X-ray beam
trajectory

• nl2dsinT
• nl/2dsinT
• Solution satisfied at specific angles (n MUST
  be an integer)

2T
14
XRD Part II

• Theoretically, almost an infinite number of
  planes can exist, but certain ones diffract more
  strongly
• Related to the atomic density both of of
  atoms and in those ions atomic density

15
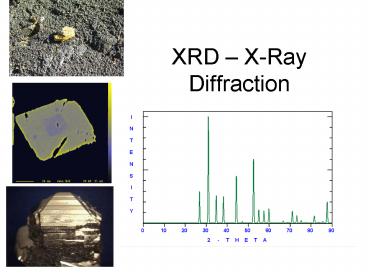
XRD results

• Diffraction pattern
• Higher symmetry ? fewer, more intense lines
  because multiple planes are complimentary
  (identical d-spacings for different planes yields
  identical diffraction)

16
pyrite
fayalite
17
XRD extinctions

• Some forms exhibit extinctions when planes
  should be present (i.e. satisfy Braggs Law) but
  are not due to destructive interference with
  another planes diffraction.
• Useful for determining special conditions of
  symmetry in a single crystal ID for body, face
  centered minerals as well as ones with screw axes
  and glide planes ? method to see differences
  between space groups

18
XRD analyses

• Can look at minerals as single crystals or as a
  powder
• Single Crystal ? must be careful about orienting
  the crystal so Braggs Law is satisfied, use
  several different techniques, advanced machines
  manipulate the sample in 3 axes (x,y,z) to
  catch all the peaks ? required for structural
  determination
• Powder has many particles with planes at many
  different orientations ? many orientations
  satisfy Braggs Law, intensities and locations
  (2T) are characteristic of specific minerals.
  Technique primarily used for identification

19
Powder XRD analyses

• With a single crystal, alignment of planes which
  give strong diffraction returns is very exact
  requires precise alignment
• With a fine powder, idea is to have crystals at a
  wide variety of orientations so hitting that
  exact alignment is possible without manipulating
  the sample i.e. in a powder we figure a few
  grains are lined up correctly

20
Powder X-ray Analyses

• XRD analysis of a powder is a common, quick, and
  relatively easy way to identify minerals.
• Having a mixture of minerals can be tricky, so
  grains are first separated if possible (small
  amounts of other minerals will give other peaks,
  but intensities are low enough that it is not a
  big deal)
• Do lose the ability to see the details of the
  structure of the mineral however as the precise
  alignment of the mineral giving the peak is
  unknown and not changeable