Atomi s vi

1
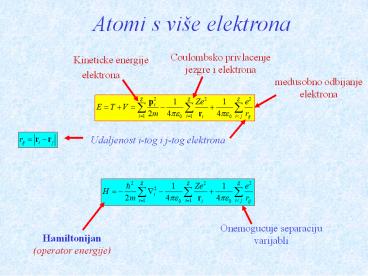
Atomi s više elektrona
Coulombsko privlacenje jezgre i elektrona
Kineticke energije elektrona
medusobno odbijanje elektrona
Udaljenost i-tog i j-tog elektrona
Onemogucuje separaciju varijabli
Hamiltonijan (operator energije)
2
Aproksimacija središnjeg polja
1. i-ti elektron osjeca usrednjen potencijal
ostalih elektron
2. Potencijal je sferno simetrican
efektivni potencijal
Schrödingerova jednadba za Z cestica se separira
na Z jednadbi za jednu cesticu!
3
Efektivni potencijal. Ovisi o svim elektronima!
Taj potencijal je pozitivan (destabilizirajuci)!
Coulombsko privlacenje jezgre (stabilizirajuce)
Položaj i-tog elektrona
Valna funkcija koja opisuje stanje i-tog
elektrona. Valna funkcija atoma (koji sadrži Z
elektrona) je produkt Z takovih funkcija!
4
Efekti penetracije i zasjenjenja (Efektivni
atomski brojevi)
Kod atoma s više elektrona svaki elektron osjeca
efektivni naboj (koji je manji od naboja jezgre)
je ga zasjenjuju ostali elektroni koji se nalaze
izmedu tog elektrona i jezgre. Što je elektron
dalje od jezgre to je taj efekat jaci!
Zefektivni
He
1.69
Na
1s 2s 2p 3s
10.6 6.85 6.85 2.20
5
Energetski nivoi atoma iste kugline funkcije
Ylm! Samo radijalni dio Rnl se mijenja!
0
3d
3d
3d
3d
3d
3p
3p
3p
E
n 3
m -2 m -1 m0 m1 m2 l2
3s
m -1 m0 m1 l1
l0
m0
2p
2p
2p
2s
n 2
m -1 m0 m1 l1
l0
m0
Efekti penetracije i zasjenjenja uklanjaju
degeneraciju stanja razlicitog angularnog momenta
(s,p,d,itd.)
1s
n 1
l0
m0
6
Paulijev princip iskljucenja
Kvantni brojevi n, l, m, ms jednoznacno odreduju
(jednoelektronsko) stanje ! U jednom stanju može
biti samo jedan elektron! (to je posljedica
drugog aksioma!)
Princip izgradnje (Aufbau princip) Popunjavanje
orbitala ide redosljedom
1s lt 2s lt 2p lt 3s lt 3p lt (4s,3d)
e.g. C atom Z6 1s22s22p2
7
Kad ne bi bilo Paulijevog principa iskljucenja
....
8
Posljedica Paulijevog principa iskljucenja
9

• Ako su na raspolaganju degenerirane orbitale,
  elektroni najprije popunjavaju prazne orbitale
  (elektrostatski razlog)

Na primjer C atom 1s22s22px2py

• Hundovo pravilo Atom poprima konfiguraciju sa
  maksimalnim brojem nesparenih elektrona
  (maksimalni multiplicitet)!

C atom je u tripletnom stanju!
10
Na kojoj udaljenosti od jezgre je najveca
vjerojatnost nalaženja 1s elektrona?
Zeff ? Z za 1s elektron minimalno zasjenjenje!
P(r) ? r2Y 2 r2 exp(-2Zr/a0)
dP/dr0 daje rmaxa0 /Z
H
He
Li
Be
C
N
O
F
Atom
rmax
0.176
0.132
0.088
0.076
0.529
0.265
0.066
0.059
(A0)
Za uran je rmax0.0058 A0 !
11
Multipliciteti stanja i simboli
termova (višecesticni sustavi)
Primjer osnovno stanje He atoma
2p
2s
E
1s
Prostorna komponenta valne funkcije je simetricna
Yprs1s(1)1s(2)
Spinska komponenta mora biti antisimetricna! To
je S0 (singlet) stanje!
Yspaa(1)b(2)-a(2)b(1)
Ukupna valna funkcija je antisimetricna! (drugi
postulat)
YYprsYspa1s(1)1s(2)a(1)b(2)-1s(1)1s(2)a(2)b(1)
12
Osnovno stanje He atoma
2p
E
2s
Y1s(1)1s(2)a(1)b(2)-1s(1)1s(2)a(2)b(1)
1s
ukupna kutna kolicina gibanja (S)
Kompaktan prikaz preko Slaterove determinante
1s(1)a(1) 1s(2)a(2) Y
1s(1)b(1) 1s(2)b(2)
multiplicitet (singlet)
1S0
ukupni angularni moment
Stupci sadrže moguca stanja jednog elektrona
Poopcenje na sustave s više od dva elektrona!
13
(prvo) Pobudeno stanje He atoma
2s
Yprs1s(1)2s(2)1s(2)2s(1)
E
Prostorne funkcije (dvije mogucnosti)
1s
Ypra1s(1)2s(2)-1s(2)2s(1)
Yspsa(1)a(2)
Yspsb(1)b(2)
Spinske funkcije (tri mogucnosti)
Yspsa(1)b(2)a(2)b(1)
Yspaa(1)b(2)-a(2)b(1)
14
Potpuna valna funkcija mora biti antisimetricna
na zamjenu dva elektrona!
2s
Singletno stanje. Simetricna prostorna i
antisimetricna spinska funkcija! Ukupni spin je
nula (S0)
Y sYprsYspa
E
1s
Singlet (1S0)
Jedna spinska funkcija. Spinski multiplicitet je
1!
Tri spinske funkcije. Spinski multiplicitet je 3!
2s
Tripletno stanje. Antisimetricna prostorna i
simetricna spinska funkcija! Ukupni spin je 1
(S1)
Y tYpraYsps
1s
triplet (3S1)
Spinski multiplicitet je 2S1!
15
Simboli termova
Primjer 2 elektrona, orbitalni angularni kvantni
brojevi l1 i l2.
Ukupni orbitalni kvantni brojevi
(Clebsch-Gordanova serija)
Ll1l2, l1l2-1,l1l2-2,...., l1-l2
Orbitalni kvantni broj sustava. Oznacava stanje
termova atoma
L0, 1, 2, 3,... S, P, D, F,...
termovi
singlet
Ukupni spinski kvantni broj S
triplet
U slucaju dva elektrona
S0, 1
16
Simboli termova
Ukupni angularni kvantni broj J
(Clebsch-Gordanova serija)
JLS, LS-1, LS-2,...., L-S
Spinski multiplicitet (singlet)
1S0
Ukupni angularni momemt (J)
term
Primjer
3P0
3P1
3P2
S1 (triplet) L1 (P)
J0
J1
J2
17
H
2s
E
H ? 2S1/2 osnovno stanje dublet S
1s
2S1/2
He
1S0 osnovno stanje singlet S
3S1 pobudeno stanje triplet S
2s
2s
1s
1s
1S0
3S1
18
Konfiguracija
elektrostatska interakcija
Ukupni orbitalni angularni momemt L
S
P
D
termovi
spinska korelacija
Spinski multiplicitet 2S1
1P
5P
3P
ukupan spin
Spin-orbit interakcija
Ukupan angularni momemt J
3P0
3P2
3P1
19
Pitanja Atomi s više elektrona