Solid angle, flux, and all that

1
Solid angle, flux, and all that

• Toby Burnett

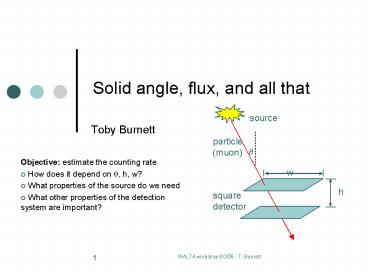
• Objective estimate the counting rate
• How does it depend on ?, h, w?
• What properties of the source do we need
• What other properties of the detection system
  are important?

2
The sourcestart with the primary flux

• A very useful reference for all cosmic
  rayshttp//pdg.lbl.gov/2005/reviews/cosmicrayrpp
  .pdf
• What is Differential flux?

3
Differential flux particles/(m2 sr s
Mev/nucleon)

• m2 the area, rate is proportional to the area
  of the detector
• sr Steradian, or solid angle. fraction of the
  sky that the detector sees
• s Just time. Leave this in for a rate.
• Mev/nucleon This is what differential means.
  We integrate over the function in the graph for a
  total, integral rate.

4
What happens in the atmosphere?

• Note the units now just flux (integrated above
  1 GeV)
• What are the depth units?
• Points are measured ?-
• Why is pn a straight line?

5
OK, now we are at the surface muons dominate

• The integral intensity of vertial muons above 1
  GeV/c at sea level is 70 m-2 s-1 sr-1

Do we understand the units here? What is p?
? Reading on, it says ..angular distribution is
? cos2? Why is that? Why are the two curves
displaced by so much?
6
The detector acceptance

• Rate is the product of the flux times the
  detector acceptance, which is an area x solid
  angle product
• Area Flux is per square meter rate is
  proportional to the area of the detector, or w2
• Solid angle The angle that, seen from the
  center of a sphere, includes a given area on the
  surface of that sphere. The value of the solid
  angle is numerically equal to the size of that
  area divided by the square of the radius of the
  sphere. ??A/r2maximum, or the whole
  sphere,is 4?

7
Detector geometry

• A muon can pass through any spot on upper and
  lower plane. Call these two points (x1,y1) and
  (x2,y2)
• The rate in these two is proportional to
• the projected area of the bottom guy,dA2 cos?
  dx2 dy2
• the solid angle subtended by the top square
  dA1/r2 (cos? dx1 dy1)/ (h/cos? )2
• That is, (cos?)4 (1/h2) dx1 dy1 dx2 dy2
• Also, the ?-dependence of the source. ( (cos?)2
  for surface muons)

8
Ok, a 4-dimensional integral now what?

• Since we know that the result is proportional to
  w2 lets set w1, so now h is the ratio of height
  to width. (Inverse of the aspect ratio.) Here is
  the integral, depending on only one
  parameter(and for now, assuming an isotropic
  source)

9
Limits

• Before we attack it, lets understand the two
  simple limits
• h0. This is just the solid angle for a plane.
  The total solid angle for the upper hemisphere is
  2?, but the average over the cos? factor is ½, so
  we get ?.
• hgtgt1. This is the solid angle of a square at a
  large distance, w2 /h2 or h-2
• An important check of our calculation is that it
  must behave like this!

10
How to do the calculation?

• Analytic
• great if a simple form exists
• Finding it can be a pain.
• Then what about the arbitrary source
  distribution?
• Hard to get a projection, like cos? distribution
• Numeric
• Multi-dimensional integrals are a pain (but the
  integrand only depends on two variablestransformi
  ng it is a pain)
• Monte Carlo
• Easiest way to do multidimensional integrals
• Need lots of trials, especially for small h.
• Projections easy

11
The answers!
?? (sr)
h/w
12
OK, how did I do it?

• Better, how can you (and your students) do such a
  calculation?
• A check for h/w1 (a cube), I get 0.628 and
  0.520
• See the Excel spreadsheet

13
Bottom line predictions for the two muon
telescopes
Telescope Adv Lab WALTA
h(m) 0.3 0.64
w(m) 0.62 0.62
Area (m2) 0.38 0.38
h/w 0.48 1.03
W( sr) 0.936 0.504
Acceptance (m2 sr) 0.36 0.19
Rate (Hz) 25 14
Measured(Hz) 20 4