Zero and Negative Exponents

1
Zero and Negative Exponents
ALGEBRA 1 LESSON 8-1
(For help, go to Lessons 1-2 and 1-6.)
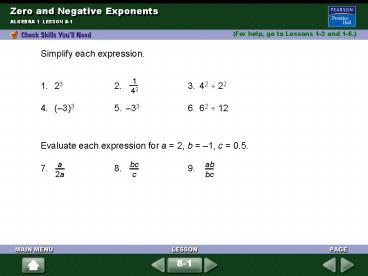
Simplify each expression.
1 42
1. 23 2. 3. 42 ? 22 4. (3)3 5. 33 6. 62 ? 12
Evaluate each expression for a 2, b 1, c
0.5.
a 2a
bc c
ab bc
7. 8. 9.
8-1
2
Zero and Negative Exponents
ALGEBRA 1 LESSON 8-1
1. 23 2 2 2 8 2. 3. 42
? 22 4 4. (3)3
(3)(3)(3) 9(3) 27 5. 33 (3 3 3)
(9 3) 27 6. 62 ? 12 36 ? 12 3 7.
for a 2 8. for b 1, c
0.5 1 9. for a 2, b 1,
c 0.5 4
Solutions
1 42
1 4 4
1 16
4 4 2 2
16 4
a 2a
2 2 2
1 2
bc c
1 0.5 0.5
ab bc
2 (1) (1) 0.5
2 0.5
8-1
3
Zero and Negative Exponents
ALGEBRA 1 LESSON 8-1
Simplify.
a.
32
(22.4)0
b.
8-1
4
Zero and Negative Exponents
ALGEBRA 1 LESSON 8-1
Simplify
a.
b.
3ab 2
8-1
5
Zero and Negative Exponents
ALGEBRA 1 LESSON 8-1
Evaluate 4x 2y 3 for x 3 and y 2.
Method 1 Write with positive exponents first.
8-1
6
Zero and Negative Exponents
ALGEBRA 1 LESSON 8-1
(continued)
Method 2 Substitute first.
8-1
7
Zero and Negative Exponents
ALGEBRA 1 LESSON 8-1
In the lab, the population of a certain bacteria
doubles every month. The expression 3000 2m
models a population of 3000 bacteria after m
months of growth. Evaluate the expression for m
0 and m 2. Describe what the value of the
expression represents in each situation.
a. Evaluate the expression for m 0.
3000 2m 3000 20   Substitute 0 for m.
3000 1 Simplify. 3000
When m 0, the value of the expression is 3000.
This represents the initial population of the
bacteria. This makes sense because when m 0, no
time has passed.
8-1
8
Zero and Negative Exponents
ALGEBRA 1 LESSON 8-1
(continued)
When m 2, the value of the expression is 750.
This represents the 750 bacteria in the
population 2 months before the present population
of 3000 bacteria.
8-1
9
Zero and Negative Exponents
ALGEBRA 1 LESSON 8-1
Simplify each expression. 1. 34 2. (6)0 3. 2a0
b2 4. 5. 8000 40 6. 4500 32
1
k m3
km3
500
8000
8-1
10
Multiplication Properties of Exponents
ALGEBRA 1 LESSON 8-3
(For help, go to Lesson 1-6.)
Rewrite each expression using exponents. 1. t
t t t t t t 2. (6 m)(6 m)(6
m) 3. (r 5)(r 5)(r 5)(r 5)(r 5) 4. 5
5 5 s s s
Simplify. 5. 54 6. (5)4 7. (5)0 8. (5)4
8-3
11
Multiplication Properties of Exponents
ALGEBRA 1 LESSON 8-3
1. t t t t t t t t7 2. (6
m)(6 m)(6 m) (6 m)3 3. (r 5)(r 5)(r
5)(r 5)(r 5) (r 5)5 4. 5 5 5 s
s s 53 s3 53s3 5. 54 (5 5 5 5)
(25 25) 625 6. (5)4 (5)(5)(5)(5)
(25)(25) 625 7. (5)0 1 8. (5)4 (
)4 ( )( )( )( ) ( )(
)
Solutions
1 5
1 5
1 5
1 5
1 5
1 25
1 25
1 625
8-3
12
Multiplication Properties of Exponents
ALGEBRA 1 LESSON 8-3
Rewrite each expression using each base only
once.
73 72
a.
44 41 42
b.
68 68
c.
8-3
13
Multiplication Properties of Exponents
ALGEBRA 1 LESSON 8-3
Simplify each expression.
p2 p p5
a.
8-3
14
Multiplication Properties of Exponents
ALGEBRA 1 LESSON 8-3
Simplify each expression.
a 2 b 4 a 5
a.
2q 3p3 4q4
b.
8-3
15
Multiplication Properties of Exponents
ALGEBRA 1 LESSON 8-3
Simplify (3 ? 103)(7 ? 105). Write the answer
in scientific notation.
8-3
16
Multiplication Properties of Exponents
ALGEBRA 1 LESSON 8-3
The speed of light is 3 ? 108 m/s. If there are1
? 103 km in 1 m, and 3.6 ? 103 s in 1 h, find
the speed of light in km/h.
8-3
17
Multiplication Properties of Exponents
ALGEBRA 1 LESSON 8-3
(continued)
The speed of light is about 1.08 ? 109 km/h.
8-3
18
Multiplication Properties of Exponents
ALGEBRA 1 LESSON 8-3
Simplify each expression. 1. 34 35 2. 4x5
3x2 3. (3 ? 104)(5 ? 102) 4. (7 ? 104)(1.5 ?
105) 5. (2w 2)(3w2b2)(5b3) 6. What is 2
trillion times 3 billion written in scientific
notation?
39
12x3
1.5 ? 107
1.05 ? 102
6 ? 1021
8-3
19
More Multiplication Properties of Exponents
ALGEBRA 1 LESSON 8-4
(For help, go to Lesson 8-3.)
Rewrite each expression using each base only
once. 1. 32 32 32 2. 23 23 23 23 3. 57
57 57 57 4. 7 7 7 Simplify. 5. x3
x3 6. a2 a2 a2 7. y2 y2 y2 8. n3 n3
8-4
20
More Multiplication Properties of Exponents
ALGEBRA 1 LESSON 8-4
1. 32 32 32 3(2 2 2) 36 2. 23
23 23 23 2(3 3 3 3) 212 3. 57 57
57 57 5(7 7 7 7) 528 4. 7 7 7
73 5. x3 x3 x(3 3) x6 6. a2 a2 a2
a(2 2 2) a6 7. y2 y2 y2 y(2
(2) (2)) y6 8. n3 n3 n(3
(3)) n6
Solutions
1 y 6
1 n 6
8-4
21
More Multiplication Properties of Exponents
ALGEBRA 1 LESSON 8-4
Simplify (a3)4.
8-4
22
More Multiplication Properties of Exponents
ALGEBRA 1 LESSON 8-4
Simplify b2(b3)2.
8-4
23
More Multiplication Properties of Exponents
ALGEBRA 1 LESSON 8-4
Simplify (4x3)2.
8-4
24
More Multiplication Properties of Exponents
ALGEBRA 1 LESSON 8-4
Simplify (4xy3)2(x3)3.
8-4
25
More Multiplication Properties of Exponents
ALGEBRA 1 LESSON 8-4
An object has a mass of 102 kg. The expression
102 (3 ? 108)2 describes the amount of resting
energy in joules the object contains. Simplify
the expression.
8-4
26
More Multiplication Properties of Exponents
ALGEBRA 1 LESSON 8-4
Simplify each expression. 1. (x4)5 2. x(x5y2)3 3
. (5x4)3 4. (1.5 ? 105)2 5. (2w2)4(3w2b2)3 6. (3
? 105)(4 ? 104)2
x20
2.25 ? 1010
125x12
432b6w2
4.8 ? 103
8-4
27
Division Properties of Exponents
ALGEBRA 1 LESSON 8-5
(For help, go to Skills Handbook page 724.)
Write each fraction in simplest
form. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11
. 12.
8-5
28
Division Properties of Exponents
ALGEBRA 1 LESSON 8-5
8-5
29
Division Properties of Exponents
ALGEBRA 1 LESSON 8-5
Simplify each expression.
a.
b.
8-5
30
Division Properties of Exponents
ALGEBRA 1 LESSON 8-5
A small dogs heart beats about 64 million beats
in a year. If there are about 530 thousand
minutes in a year, what is its average heart rate
in beats per minute?
The dogs average heart rate is about 121 beats
per minute.
8-5
31
Division Properties of Exponents
ALGEBRA 1 LESSON 8-5
3 y 3
4
Simplify .
8-5
32
Division Properties of Exponents
ALGEBRA 1 LESSON 8-5
2 3
3
a. Simplify .
8-5
33
Division Properties of Exponents
ALGEBRA 1 LESSON 8-5
(continued)
b. Simplify .
8-5
34
Division Properties of Exponents
ALGEBRA 1 LESSON 8-5
Simplify each expression. 1. 2. 3. 4. 5. 6.
1 w4
a10
27
1.6 ? 1034 ? 102
3
2
4x 3 3x 2
24 5
27 64x3
4 ? 104
8-5
35
Geometric Sequences
ALGEBRA 1 LESSON 8-6
(For help, go to Lesson 5-6.)
Find the common difference of each
sequence. 1. 1, 3, 5, 7, ... 2. 19, 17, 15, 13,
... 3. 1.3, 0.1, 1.1, 2.3, ... 4. 18, 21.5, 25,
28.5, ... Use inductive reasoning to find the
next two numbers in each pattern. 5. 2, 4, 8,
16, ... 6. 4, 12, 36, ... 7. 0.2, 0.4, 0.8, 1.6,
... 8. 200, 100, 50, 25, ...
8-6
36
Geometric Sequences
ALGEBRA 1 LESSON 8-6
1. 1, 3, 5, 7, ... 2. 19, 17, 15, 13, ... 7
5 2, 5 3 2, 3 1 2 13 15 2, 15
17 2, Common difference 2 17 19
2 Common difference 2 3. 1.3, 0.1, 1.1,
2.3, ... 4. 18, 21.5, 25, 28.5, ... 2.3
(1.1) 1.2, 1.1 28.5 25 3.5, 25 21.5
3.5, 0.1 1.2, 0.1 1.3 1.2 21.5 18
3.5 Common difference 1.2 Common
difference 3.5
Solutions
8-6
37
Geometric Sequences
ALGEBRA 1 LESSON 8-6
5. 2, 4, 8, 16, ... 6. 4, 12, 36, ... 2(2)
4, 4(2) 8, 8(2) 16, 4(3) 12, 12(3) 36,
16(2) 32, 32(2) 64 36(3) 108, 108(3)
324 Next two numbers 32, 64 Next two numbers
108, 324 7. 0.2, 0.4, 0.8, 1.6, ... 8. 200,
100, 50, 25, ... (0.2)2 0.4, 0.4(2) 0.8,
0.8(2) 200 ? 2 100, 100 ? 2 50, 1.6,
1.6(2) 3.2, 3.2(2) 6.4 50 ? 2 25, 25 ? 2
12.5, Next two numbers 3.2, 6.4 12.5 ? 2 6.25
Solutions (continued)
8-6
38
Geometric Sequences
ALGEBRA 1 LESSON 8-6
Find the common ratio of each sequence.
a. 3, 15, 75, 375, . . .
The common ratio is 5.
8-6
39
Geometric Sequences
ALGEBRA 1 LESSON 8-6
Find the next three terms of the sequence 5,
10, 20, 40, . . .
The common ratio is 2.
The next three terms are 40(2) 80, 80(2)
160, and 160(2) 320.
8-6
40
Geometric Sequences
ALGEBRA 1 LESSON 8-6
Determine whether each sequence is arithmetic or
geometric.
a. 162, 54, 18, 6, . . .
The sequence has a common ratio.
The sequence is geometric.
8-6
41
Geometric Sequences
ALGEBRA 1 LESSON 8-6
(continued)
b. 98, 101, 104, 107, . . .
The sequence has a common difference.
The sequence is arithmetic.
8-6
42
Geometric Sequences
ALGEBRA 1 LESSON 8-6
Find the first, fifth, and tenth terms of the
sequence that has the rule A(n) 3(2)n 1.
first term A(1) 3(2)1 1 3(2)0 3(1)
3
fifth term A(5) 3(2)5 1 3(2)4 3(16)
48
tenth term A(10) 3(2)10 1 3(2)9
3(512) 1536
8-6
43
Geometric Sequences
ALGEBRA 1 LESSON 8-6
Suppose you drop a tennis ball from a height of
2 meters. On each bounce, the ball reaches a
height that is 75 of its previous height. Write
a rule for the height the ball reaches on each
bounce. In centimeters, what height will the ball
reach on its third bounce?
8-6
44
Geometric Sequences
ALGEBRA 1 LESSON 8-6
(continued)
The ball drops from an initial height, for which
there is no bounce. The initial height is 200 cm,
when n 1. The third bounce is n 4. The common
ratio is 75, or 0.75.
The height of the third bounce is 84.375 cm.
8-6
45
Geometric Sequences
ALGEBRA 1 LESSON 8-6
1. Find the common ratio of the geometric
sequence 3, 6, 12, 24, . . . 2. Find the
next three terms of the sequence 243, 81, 27, 9,
. . . 3. Determine whether each sequence is
arithmetic or geometric. a. 37, 34, 31, 28, . .
. b. 8, 4, 2, 1, . . . 4. Find the
first, fifth, and ninth terms of the sequence
that has the rule A(n) 4(5)n1. 5. Suppose you
enlarge a photograph that is 4 in. wide and 6 in.
long so that its dimensions are 20 larger than
its original size. Write a rule for the length of
the copies. What will be the length if you
enlarge the photograph five times? (Hint The
common ratio is not just 0.2. You must add 20 to
100.)
2
arithmetic
geometric
4, 2500, 1,562,500
A(n) 6(1.2)n-1 about 14.9 in.
8-6