Graphing Systems of Equations

1
Graphing Systems of Equations
ALGEBRA 2 LESSON 3-1
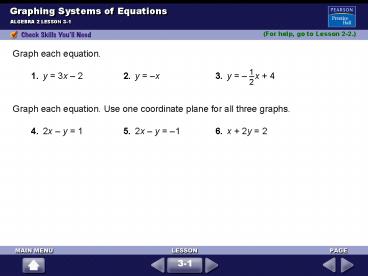
(For help, go to Lesson 2-2.)
3-1
2
Graphing Systems of Equations
ALGEBRA 2 LESSON 3-1
Solutions
1. y 3x 2 2. y x slope 3 slope
1 y-intercept 2 y-intercept 0 3. y
x 4 4. 2x y 1 slope y 2x
1 y-intercept 4 y 2x 1 5. 2x y
1 6. x 2y 2 y 2x 1 2y x
2 y 2x 1 y x 1
1 2
1 2
1 2
3-1
3
Graphing Systems of Equations
ALGEBRA 2 LESSON 3-1
Solve the system by graphing.
Check Show that (4, 2) makes both equations
true.
3-1
4
Graphing Systems of Equations
ALGEBRA 2 LESSON 3-1
The table shows the number of pairs of shoes
sold by two new employees at a shoe store. Find
linear models for each employees sales. Graph
the data and models. Predict the week in which
they could sell the same number of pairs of shoes.
Step 1  Let x number of weeks. Let y number
of shoes sold.
Use the LinReg feature of the graphing calculator
to find linear models. Rounded versions appear
below.
Eds rate y 5.9x 44 Jos rate y 7.5x
32.5
3-1
5
Graphing Systems of Equations
ALGEBRA 2 LESSON 3-1
(continued)
If the trends continue, the number of pairs of
shoes that Ed and Jo will sell will be equal in
about week 7.
3-1
6
Graphing Systems of Equations
ALGEBRA 2 LESSON 3-1
Classify the system without graphing.
Since the slopes are the same, the lines could be
the same or coinciding.
Compare the y-intercepts.
Since the y-intercepts are the same, the lines
coincide.
It is a dependent system.
3-1
7
Graphing Systems of Equations
ALGEBRA 2 LESSON 3-1
1. Graph and solve the system. Classify
each system without graphing. Tell how many
solutions there are. 2. 3. 4.
dependent infinitely many
inconsistent no solutions
independent one solution
3-1
8
Solving Systems Algebraically
ALGEBRA 2 LESSON 3-2
(For help, go to Lesson 1-1 and 1-3.)
Find the additive inverse of each
term. 1. 4 2. x 3. 5x 4. 8y Let x 2y 1.
Substitute this expression for x in each
equation. Solve for y. 5. x 2y 3 6. y 2x
8 7. 2y 3x 5
3-2
9
Solving Systems Algebraically
ALGEBRA 2 LESSON 3-2
Solutions
3-2
10
Solving Systems Algebraically
ALGEBRA 2 LESSON 3-2
Solve the system by substitution.
Step 1  Solve for one of the variables. Solving
the first equation for x is the easiest. x
3y 12 x 3y 12
Step 2  Substitute the expression for x into the
other equation. Solve for y.
2x 4y 9 2(3y 12) 4y
9 Substitute for x. 6y 24 4y
9 Distributive Property 6y 4y
33 y 3.3
Step 3  Substitute the value of y into either
equation. Solve for x. x 3(3.3) 12 x
2.1
The solution is (2.1, 3.3).
3-2
11
Solving Systems Algebraically
ALGEBRA 2 LESSON 3-2
At Renaldis Pizza, a soda and two slices of the
pizzaoftheday costs 10.25. A soda and four
slices of the pizzaoftheday costs 18.75. Find
the cost of each item.
2p s 10.25 Solve for one of the
variables. s 10.25 2p  
3-2
12
Solving Systems Algebraically
ALGEBRA 2 LESSON 3-2
(continued)
4p (10.25 2p) 18.75 Substitute the
expression for s into the other equation.
Solve for p. p 4.25
2(4.25) s 10.25 Substitute the value of p
into one of the equations. Solve for s.
s 1.75
The price of a slice of pizza is 4.25, and the
price of a soda is 1.75.
3-2
13
Solving Systems Algebraically
ALGEBRA 2 LESSON 3-2
Use the elimination method to solve the system.
y 3
3x y 9 Choose one of the original
equations.
3x (3) 9 Substitute y. Solve for x.
x 2
The solution is (2, 3).
3-2
14
Solving Systems Algebraically
ALGEBRA 2 LESSON 3-2
Solve the system by elimination.
To eliminate the n terms, make them additive
inverses by multiplying.
m 4 Solve for m.
2m 4n 4 Choose one of the original
equations. 2(4) 4n 4 Substitute for
m. 8 4n 4
4n 12 Solve for n. n 3
The solution is (4, 3).
3-2
15
Solving Systems Algebraically
ALGEBRA 2 LESSON 3-2
Solve each system by elimination.
a. 3x 5y 6 6x 10y 0
Elimination gives an equation that is always
false.
The two equations in the system represent
parallel lines.
The system has no solution.
3-2
16
Solving Systems Algebraically
ALGEBRA 2 LESSON 3-2
Solve each system by elimination.
b. 3x 5y 6 6x 10y 12
Elimination gives an equation that is always true.
The two equations in the system represent the
same line.
The system has an infinite number of solutions
3-2
17
Solving Systems Algebraically
ALGEBRA 2 LESSON 3-2
(9, 4)
cookbook 25 novel 14
(3, 5)
(6.5, 5.5)
no solutions
3-2
18
Systems of Inequalities
ALGEBRA 2 LESSON 3-3
(For help, go to Lessons 1-4, 2-5, and 2-7.)
3-3
19
Systems of Inequalities
ALGEBRA 2 LESSON 3-3
Solutions
1. 5x 6 gt 27 2. 18 5y 52 5x gt
33 5y 70 x gt y 14 or
x gt 6 3. 5(4x 1) lt 23 4. y 4x 1 20x
5 lt 23 20x lt 28 x gt x gt or x gt
1
33 5
3 5
28 20
7 5
2 5
3-3
20
Systems of Inequalities
ALGEBRA 2 LESSON 3-3
3-3
21
Systems of Inequalities
ALGEBRA 2 LESSON 3-3
Solve the system of inequalities.  
Graph each inequality. First graph the boundary
lines. Then decide which side of each boundary
line contains solutions and whether the boundary
line is included.
3-3
22
Systems of Inequalities
ALGEBRA 2 LESSON 3-3
(continued)
Every point in the red region above the dashed
line is a solution of x y gt 1.
Every point in the blue region above the dashed
line is a solution of x y gt 3.
Every point in the purple region where the red
and blue regions intersect is a solution of the
system. For example (2, 2) is a solution.
3-3
23
Systems of Inequalities
ALGEBRA 2 LESSON 3-3
Jenna spends at most 150 min a night on math and
science homework. She spends at least 60 min on
math. Write and solve a system of inequalities to
model how she allots her time for these two
subjects.
3-3
24
Systems of Inequalities
ALGEBRA 2 LESSON 3-3
(continued)
The region of overlap is a graph of the solution.
3-3
25
Systems of Inequalities
ALGEBRA 2 LESSON 3-3
Solve the system of inequalities.  
Every point in the blue region above the dashed
line is a solution of y gt x 2 5.
3-3
26
Systems of Inequalities
ALGEBRA 2 LESSON 3-3
(continued)  
Every point in the purple region where the red
and blue regions intersect is a solution of the
system. For example (4, 4) is a solution.
3-3
27
Systems of Inequalities
ALGEBRA 2 LESSON 3-3
1. Solve the system of inequalities by
graphing. 2. A 24hour radio station plays
only classical music, jazz, talk programs, and
news. It plays at most 12 h of music per day,
of which at least 4 h is classical. Jazz gets at
least 25 as much time as classical. Write and
graph a system of inequalities. 3. Solve the
system of inequalities by graphing.
3-3
28
Linear Programming
ALGEBRA 2 LESSON 3-4
(For help, go to Lessons 3-2 and 3-3.)
3-4
29
Linear Programming
ALGEBRA 2 LESSON 3-4
Solutions
3-4
30
Linear Programming
ALGEBRA 2 LESSON 3-4
Solutions (continued)
4. 5. 6.
3-4
31
Linear Programming
ALGEBRA 2 LESSON 3-4
Find the values of x and y that maximize and
minimize P if P 5x 4y.
Step 2 Find the coordinates for each vertex.
3-4
32
Linear Programming
ALGEBRA 2 LESSON 3-4
(continued)
Step 3 Evaluate P at each vertex.
Vertex P 5x 4y A(1, 3) P 5(1) 4(3)
7 B(5, 4) P 5(5) 4(4) 9 C(4, 1) P
5(4) 4(1) 16
When x 1 and y 3, P has its maximum value of
7. When x 4 and y 1, P has its minimum value
of 16.
3-4
33
Linear Programming
ALGEBRA 2 LESSON 3-4
A furniture manufacturer can make from 30 to 60
tables a day and from 40 to 100 chairs a day. It
can make at most 120 units in one day. The profit
on a table is 150, and the profit on a chair is
65. How many tables and chairs should they make
per day to maximize profit? How much is the
maximum profit?
3-4
34
Linear Programming
ALGEBRA 2 LESSON 3-4
(continued)
x 30 x 60 y 40 y 100 x y 120
Write Write the constraints. Write the objective
function.
P 150x 65y
Step 2 Find the coordinates of each
vertex. Vertex A(30, 90) B(60, 60) C(60,
40) D(30, 40)
Step 3 Evaluate P at each vertex. P 150x
65y P 150(30) 65(90) 10,350 P 150(60)
65(60) 12,900 P 150(60) 65(40) 11,600 P
150(30) 65(40) 7100
The furniture manufacturer can maximize their
profit by making 60 tables and 60 chairs. The
maximum profit is 12,900.
3-4
35
Linear Programming
ALGEBRA 2 LESSON 3-4
1. Graph the system of constraints. Name all
vertices of the feasible region. Then find the
values of x and y that maximize and minimize the
objective function P 2x 7y 4. 2 x
4 1 y 3 y x 2. If the
constraint on y in the system for Question 1 is
changed to 1 lt y lt 3, how does the minimum
value for the objective function change?
5 3
2 3
There is a new minimum value of 13 when x 1 and
y 1.
3-4
36
Graphs in Three Dimensions
ALGEBRA 2 LESSON 3-5
(For help, go to Lessons 2-2.)
Find the x- and y-intercepts of the graph of each
linear equation. 1. y 2x 6 2. 2x 9y
36 3. 3x 8y 24 4. 4x 5y 40 Graph each
linear equation. 5. y 3x 6. y 2x
4 7. 4y 3x 8 8. 3x 2y 7
3-5
37
Graphs in Three Dimensions
ALGEBRA 2 LESSON 3-5
Solutions
1. xintercept (let y 0)     yintercept
(let x 0) y 2x 6 y 2x 6 0 2x
6 y 2(0) 6 2x 6 y 6 x
3 2. xintercept (let y 0)     yintercept
(let x 0) 2x 9y 36 2x 9y
36 2x 9(0) 36 2(0) 9y 36 2x
36 9y 36 x 18 y
4 3. x-intercept 8      y-intercept
3 4. x-intercept 10  
   y-intercept 8
3-5
38
Graphs in Three Dimensions
ALGEBRA 2 LESSON 3-5
Solutions (continued)
3-5
39
Graphs in Three Dimensions
ALGEBRA 2 LESSON 3-5
Graph each point in the coordinate space.
a. (3, 3, 4) Sketch the axes.
b. (3, 4, 2) Sketch the axes.
3-5
40
Graphs in Three Dimensions
ALGEBRA 2 LESSON 3-5
In the diagram, the origin is at the center of a
cube that has edges 6 units long. The x-, y-, and
z-axes are perpendicular to the faces of the
cube. Give the coordinates of the corners of the
cube.
3-5
41
Graphs in Three Dimensions
ALGEBRA 2 LESSON 3-5
Sketch the graph of 3x 2y z 6.
Step 1  Find the intercepts.
3x 2y z 6 3x 2(0) (0) 6 To
find the x-intercept, substitute 0 for y and z.
3x 6
x 2 The x-intercept is 2.
3(0) 2y (0) 6 To find the y-intercept,
substitute 0 for x and z.
2y 6 y 3 The
y-intercept is 3.
3(0) 2(0) z 6 To find the z-intercept,
substitute 0 for x and y.
z 6 The z-intercept is 6.
3-5
42
Graphs in Three Dimensions
ALGEBRA 2 LESSON 3-5
(continued)
Step 2 Graph the intercepts.
Each point on the plane represents a solution to
3x 2y z 6.
3-5
43
Graphs in Three Dimensions
ALGEBRA 2 LESSON 3-5
Graph each point in coordinate space. 1. (2,
3, 5) 2. (0, 4, 2) 3. Graph 2x 4y
4z 12.
3-5
44
Systems With Three Variables
ALGEBRA 2 LESSON 3-6
(For help, go to Lessons 3-1 and 3-2.)
Solve each system. 1. 2. 3. Let y 4x
2. Solve each equation for x. 4. 3x y
5 5. x 2y 3 6. 4x 3y 2 Verify that the
given ordered pair is a solution of each equation
in the system. 7. (1, 3) 8. (4, 2)
3-6
45
Systems With Three Variables
ALGEBRA 2 LESSON 3-6
3-6
46
Systems With Three Variables
ALGEBRA 2 LESSON 3-6
Solutions (continued)
3-6
47
Systems With Three Variables
ALGEBRA 2 LESSON 3-6
Solve the system by elimination. 
Step 1  Pair the equations to eliminate z,
because the terms are already additive inverses.
Step 2  Write the two new equations as a system.
Solve for x and y.
3-6
48
Systems With Three Variables
ALGEBRA 2 LESSON 3-6
(continued)
The solution of the system is (2, 5, 7).
3-6
49
Systems With Three Variables
ALGEBRA 2 LESSON 3-6
(continued)
3-6
50
Systems With Three Variables
ALGEBRA 2 LESSON 3-6
Solve the system by elimination.
Step 1  Pair the equations to eliminate x.
Step 2  Write the two new equations as a system.
Solve for y and z.
3-6
51
Systems With Three Variables
ALGEBRA 2 LESSON 3-6
(continued)
9y 22z 7 9y 22(4) 7 Substitute the
value of z. y 9
The solution of the system is (1, 9, 4).
3-6
52
Systems With Three Variables
ALGEBRA 2 LESSON 3-6
Solve the system by substitution.
Step 1  Choose one equation to solve for one
of its variables.
Step 2  Substitute the expression for x into
each of the other two equations.
3-6
53
Systems With Three Variables
ALGEBRA 2 LESSON 3-6
(continued)
Step 3  Write the two new equations as a system.
Solve for y and z.
3-6
54
Systems With Three Variables
ALGEBRA 2 LESSON 3-6
(continued)
The solution of the system is (7, 9, 1)
3-6
55
Systems With Three Variables
ALGEBRA 2 LESSON 3-6
You have 10,000 in a savings account. You want
to take most of the money out and invest it in
stocks and bonds. You decide to invest nine times
as much as you leave in the account. You also
decide to invest five times as much in stocks as
in bonds. How much will you invest in stocks, how
much in bonds, and how much will you leave in
savings?
3-6
56
Systems With Three Variables
ALGEBRA 2 LESSON 3-6
(continued)
Write k b s 10000 k b 9
s k 5 b   
Step 2 Write the two new equations as a system.
Solve for b and s.
3-6
57
Systems With Three Variables
ALGEBRA 2 LESSON 3-6
(continued)
You should invest 7,500 in stocks, 1,500 in
bonds, and leave 1,000 in savings.
3-6
58
Systems With Three Variables
ALGEBRA 2 LESSON 3-6
(3, 7, 4)
(2, 11, 5)
(3, 5, 2)
3-6