NFA vs DFA - PowerPoint PPT Presentation
Title:
NFA vs DFA
Description:
Suppose that = { a, b} and we have only a transition for a: q. qi. a. qj. What should we do for b? ... What needs to be shown to prove that M and M' are equivalent? ... – PowerPoint PPT presentation
Number of Views:1096
Avg rating:3.0/5.0
Title: NFA vs DFA
1
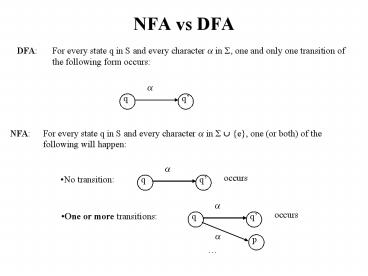
NFA vs DFA
For every state q in S and every character ? in
?, one and only one transition of the following
form occurs
DFA
?
q
q
For every state q in S and every character ? in ?
? e, one (or both) of the following will happen
NFA
2
NFA vs DFA (2)
All deterministic automata are non deterministic
Given a nondeterministic automaton, it is always
possible to find a an equivalent deterministic
automaton doing the same?
That is, given an NFA M (Q,?, ?,s,F) does there
exists an equivalent DFA M (Q,?, ?,s,F)?
YES!
We are going to construct the DFA by using the
given NFA
3
Equivalence of NFA and DFA
Definition. Two automata A and A are equivalent
if they recognize the same language.
Theorem. Given any NFA A, then there exists a DFA
A such that A is equivalent to A
4
Idea of the Transformation NFA ? DFA
We would like
For every transition in NFA
?
qj
q
qi
where Qi (or Qj) is related to qi (or qj)
5
Idea (2) Remove Non Determinism
DFA
NFA
q1
?
q2
?
q
q
?
qn
The states in the DFA will be elements in ?(Q)
?(q, ?)
6
Step 1 Assign Arcs
DFA
p1
q1
p2
q2
?
pm
qn
7
Step 1 Variation
Let S be an state formed by q1, q2, , qn, we
denote the set ?(S, ?) as the set of all states
that are reachable from states in S by reading ?
DFA
q1
q2
?
?(S, ?)
qn
8
Step 2 Eliminating e-Transitions
P
P
e
e
e
?
?(S, ?)
9
Step 3 Handling Undetermined Transitions
Suppose that ? a, b and we have only a
transition for a
NFA
a
qj
q
qi
What should we do for b?
DFA
10
Step 4 Determining Favorable States
We will make states favorable in the DFA only if
they contain at least one state which is
favorable in the NFA
11
Examples
a
r
r
s
q
q
gt
b
b
b
a
r
r
s
q
q
gt
e
b
b
12
Proof
Given an NFA M (Q,?,?,s,F) suppose that we use
the procedure discussed to obtain a DFA M
(Q,?, ?,s,F). What needs to be shown to prove
that M and M are equivalent?
- For each w accepted by M, w is also accepted by
the NFA - For each w accepted by M, w is also accepted by
the DFA
13
Proof (2)
- Proof by induction on the length n of the word
- w ?1 ?2 ?n
- n 1
- n k ? n k1
14
Construction
D
q1
q2
?
?(S, ?)
qm
Where S q1, q2, , qm,
Assume no e-transitions for the moment
15
DFA
?1
?2
?n
We have
s
s1
sn
We want
s1 ?(s, ?1)
sn-1 ?(sn-2, ?n-1)
sn ?(sn-1, ?n)
qn is favorable in DFA
16
Dealing with e-transitions
P
P
e
e
e
?
?(S, ?)
17
DFA
?1
?2
?n
We have
s
s1
sn
We want
m ? n
each ?i is either an ?j or e
18
Main Result
The other direction is very simple (do it!)
For each w accepted by N, w is also accepted
by D
Theorem. Given any NFA N, then there exists a DFA
D such that N is equivalent to D
19
Homework for Friday Sep. 14
- Write formally the NFA of Slide 5 in NFA.ppt
(class about nondeterministic automata) - That is, write each of the elements of (Q,?,
?,s,F). - Use the procedure described in this class or the
one in the book (they have some small
differences) to obtain the DFA equivalent to the
NFA that is on top of Slide 12 - Also explain in words why these two automata are
equivalent - Exercise 1.11
- Problem 1.31
- Problem 1.37 (so for example, C3 is the set of
all binary numbers that are multiples of 3
including 0, 11, 110, 1001, )