Viewing geometry - PowerPoint PPT Presentation
Title:
Viewing geometry
Description:
Reflectance functions Representing surface orientation using stereographic projection Reflectance Map R(f,g) ... – PowerPoint PPT presentation
Number of Views:69
Avg rating:3.0/5.0
Title: Viewing geometry
1
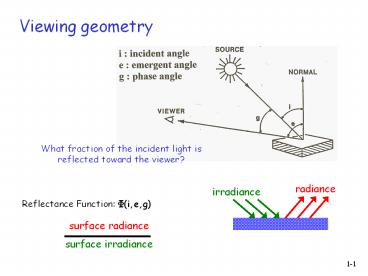
Viewing geometry
What fraction of the incident light is reflected
toward the viewer?
radiance
irradiance
Reflectance Function F(i,e,g)
surface radiance surface irradiance
2
Reflectance functions
Fmirror(i,e,g) 1 if i e i e g
0 otherwise
Fmatte(i,e,g) ? cos i if i lt 90 0
otherwise ? albedo
3
Representing surface orientation using
stereographic projection
sphere has radius 1
g
f
(f,g) (0, 2)
(f,g) (2, 0)
viewer
4
Reflectance Map R(f,g)
Given (1) light source (2) viewer position (3)
surface reflectance properties
R(f,g) relates brightness to surface orientation
Image Irradiance Equation I(x,y) I0 ?(x,y)
R(f,g)
5
Ikeuchi Horn shape-from-shading algorithm
- Three sources of constraint
- (1) image intensity I(x,y)
- (2) surface smoothness
- e.g. minimize total variation in surface
- (3) points of known surface orientation
- e.g. occluding boundaries, shadow boundaries
(known viewer direction, light source direction,
surface reflectance properties)
I(x,y) I0 ?(x,y) R(f,g)
6
Simplified Ikeuchi Horn algorithm
- Construct initial solution with f g 0
everywhere, except at points of known surface
orientation (e.g. occluding boundary) - Let fi(x,y) gi(x,y) denote surface
orientations at iteration i - To determine fi1(x,y) gi1(x,y)
- For each location (x,y)
- (1) Compute the average value of fi(x,y) in a
neighborhood around (x,y) f - (2) Compute the average value of gi(x,y) in a
neighborhood around (x,y) g - (3) Find the contour of possible f and g values
in R(f,g) that are consistent with I(x,y) - (4) Find the point on this contour that is
closest to the surface orientation given
by (f,g) the coordinates of this point
represent the new surface orientation for
location (x,y) fi1(x,y) gi1(x,y)
7
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0.1 0.1 0.1 0.1 0 0 0
0 0 0 0 0.2 0.4 0.4 0.3 0.2 0.1 0 0
0 0 0 0.2 0.3 0.5 0.7 0.6 0.3 0.2 0.1 0
0 0 0 0.2 0.3 0.6 0.8 0.9 0.6 0.2 0.2 0
0 0 0 0.3 0.4 0.7 0.9 1.0 0.8 0.5 0.3 0
0 0 0 0.3 0.4 0.7 0.9 1.0 0.8 0.5 0.3 0
0 0 0 0.2 0.3 0.6 0.8 0.9 0.6 0.2 0.2 0
0 0 0 0.2 0.3 0.5 0.7 0.6 0.3 0.2 0.1 0
0 0 0 0 0.2 0.4 0.4 0.3 0.2 0.1 0 0
0 0 0 0 0 0.1 0.1 0.1 0.1 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
image of shaded sphere
8
(0,0) (0.0) (0,0) (0,0) (0,0) (0,2) (0,2) (,) (0,0) (0,0) (0,0) (0,0)
(0,0) (0,0) (0,0) (0,0) (,) (0,0) (0,0) (0,0) (,) (0,0) (0,0) (0,0)
(0,0) (0,0) (0,0) (,) (0,0) (0,0) (0,0) (0,0) (0,0) (,) (0,0) (0,0)
(0,0) (0,0) (0,0) (,) (0,0) (0,0) (0,0) (0,0) (0,0) (0,0) (,) (0,0)
(0,0) (0,0) (,) (0,0) (0,0) (0,0) (0,0) (0,0) (0,0) (0,0) (0,0) (,)
(0,0) (0,0) (,) (0,0) (0,0) (0,0) (0,0) (0,0) (0,0) (0,0) (0,0) (2,0)
(0,0) (0,0) (,) (0,0) (0,0) (0,0) (0,0) (0,0) (0,0) (0,0) (0,0) (2,0)
(0,0) (0,0) (,) (0,0) (0,0) (0,0) (0,0) (0,0) (0,0) (0,0) (0,0) (,)
(0,0) (0,0) (0,0) (,) (0,0) (0,0) (0,0) (0,0) (0,0) (0,0) (,) (0,0)
(0,0) (0,0) (0,0) (,) (0,0) (0,0) (0,0) (0,0) (0,0) (,) (0,0) (0,0)
(0,0) (0,0) (0,0) (0,0) (,) (0,0) (0,0) (0,0) (,) (0,0) (0,0) (0,0)
(0,0) (0,0) (0,0) (0,0) (0,0) (0,-2) (0,-2) (,) (0,0) (0,0) (0,0) (0,0)
surface orientation (f,g) initial state
9
Koenderink colleagues
Subjects qualitative impressions of shape were
consistent, but subjects differed quantitatively
in amount of depth perceived Analysis is not
strictly local global factors play a role