Concordance model

1

• Concordance model

2
Critical Tests of the Standard Model of
CosmologyGeorge F R EllisUniversity of Cape
TownUnity of the Universe Meeting

• ICG,Portsmouth
• June 2009

3
1 The consensus model

• We now have a consensus standard model of
  cosmology, based on the Robertson-Walker
  geometries and standard physics.
• It seems to fit the observations well.
• However it has some mysteries.
• We need to test it to check its foundations.

4
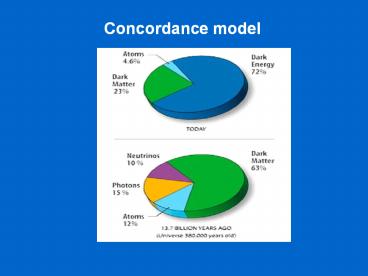
Visible
Invisible
The canonical picture (WMAP)
5

• OBSERVABLE UNIVERSE
• 1 Baryons (4) and structure formation
• Radiation emitted and absorbed
• Major part of observational cosmology/astronomy
• 2 Dark matter (23) and structure formation
• No radiation emitted or absorbed
• Indirectly observed major part of what is
• 3 Dark energy (73) and cosmology
• No radiation emitted and absorbed
• Existence inferred dominant energy form
• PRE-OBSERVABLE UNIVERSE
• Interactions and geometry inferred
• Tested through relics (matter, radiation)

6
2 The Acceleration of the universe

• The explanation of dark energy is a central
  pre-occupation of present day cosmology.
• Its presence is indicated by the recent speeding
  up of the expansion of the universe indicated by
  supernova observations
• confirmed by other observations such as those of
  the cosmic background radiation anisotropies and
  LSS/BAO studies
• Its nature (whether constant, or varying) is a
  major problem for theoretical physics
• Not uniquely related to any known field or
  particles
• NB discovered, not predicted!

7
The Acceleration of the universe
8
Lab tests of Dark energy?

• Experimental detection of dark energy in a lab or
  even the solar system is not feasible, for the
  usual conception of DE as cosmological constant
  or quintessence
• CONTRAST With Dark Matter NO LAB TESTS
• But Unified approaches to DE and DM need to be
  explored they may be facets of the same problem
• Towards a unifying scalar field?
• Then evidence for dark matter is also evidence
  for dark energy
• But then changing (with scale) from attraction to
  repulsion why and how? Can we test that change?
• NO!

9

• Without lab tests rely on theoretical
  explorations and explanations for its nature
• Cosmological constant but then10120 too small!
• Theoretical disaster!
• Quintessence unknown nature
• (arbitrary equation of state)
• Modified gravitational theories
• higher curvature terms
• Effects of higher dimensions
• ????

10

• But how do we test these theoretical proposals?
• Many seem very arbitrary
• Just writing down a Lagrangian does not prove
  such matter exists!
• If the explanation only explains one thing
  (acceleration) and has no other testable outcome,
  it is an ad hoc explanation for that one thing
  rather than a unifying scientific proposal
• Unity of universe is missing!
• Needs some other independent experimental or
  observational test but we dont have another
  viable context for applying such tests
• So how do we justify our proposed theoretical
  explanations?
• Why this form of quintessence?
• Why a cosmological constant?

11

• 3 A Multiverse?
• Data is consistent with cosmological constant
• The major theoretical proposal to explain the
  force causing acceleration is via a multiverse
• The idea of a multiverse -- an ensemble of
  universes or of universe domains has received
  increasing attention in cosmology Andrei
  Lindes talk
•   - separate places chaotic inflation
• Vilenkin, Linde, Guth, Weinberg
•    
•  - the Everett quantum multi-universe other
  branches of the wavefunction Deutsch
• - the cosmic landscape of string theory,
  imbedded in a chaotic cosmology Susskind

12
(No Transcript)
13

• Application explaining fundamental
  constants
• Explaining the small value of the
  cosmological constant
• by anthropic argument Steven Weinberg
  astro-ph/0005265 Susskind, The Cosmic Landscape
• A multiverse with varied local physical
  properties is one possible scientific
  explanation
• an infinite set of universe domains allows all
  possibilities to occur, so somewhere things work
  out OK
• NB it must be an actually existing multiverse -
  this is essential for any such anthropic argument
• - too large a value for ? results in no
  structure and hence no life, so anthropic
  considerations mean that the value of ? we
  observe will be small in fundamental units
• - thus justifying an actual value extremely
  different from the natural one predicted by
  physics 120 orders of magnitude

14

• Our Cosmic HabitatMartin Rees

Rees explores the notion that our universe is
just a part of a vast ''multiverse,'' or ensemble
of universes, in which most of the other
universes are lifeless. What we call the laws of
nature would then be no more than local bylaws,
imposed in the aftermath of our own Big Bang. In
this scenario, our cosmic habitat would be a
special, possibly unique universe where the
prevailing laws of physics allowed life to
emerge.
15

• The Cosmic Landscape String Theory and the
  Illusion of Intelligent DesignLeonard Susskind

Susskind concludes that questions such as "why is
a certain constant of nature one number rather
than another?" may well be answered by "somewhere
in the megaverse the constant equals this number
somewhere else it is that number. We live in one
tiny pocket where the value of the constant is
consistent with our kind of life. Thats it!
Thats all. There is no other answer to the
question". The anthropic principle is thus
rendered respectable and intelligent design is
just an illusion
16

• Is this science, or scientifically based
  philosophy?
• Two central scientific virtues are testability
  and explanatory power. In the cosmological
  context, these are often in conflict with each
  other.
• The extreme case is multiverse proposals, where
  no direct observational tests of the hypothesis
  are possible, as the supposed other universes
  cannot be seen by any observations whatever, and
  the assumed underlying physics is also untested
  and indeed probably untestable.
• In this context one must re-evaluate what the
  core of science is can one maintain one has a
  genuine scientific theory when direct and indeed
  indirect tests of the theory are impossible?
• If one claims this, one is altering what one
  means by science. One should be very careful
  before so doing.

17

• The key observational point is that the domains
  considered are beyond the particle horizon and
  are therefore unobservable.
• See the diagrams of our past light cone by Mark
  Whittle (Virginia)

18

• Expand the spatial distances to see the causal
  structure (light cones at 45o)

Observable
Start of universe
19

• Now it is clear what the observational and causal
  limits are
• No
  observational data whatever are available!
• Better scale
• The assumption is we that can extrapolate to 100
  Hubble radii, 101000
• Hubble radii, or much much more (infinity)

20

• ?? Implied by known physics that leads to chaotic
  inflation
• The key physics (Coleman-de Luccia tunneling, the
  string theory landscape) is extrapolated from
  known and tested physics to new contexts the
  extrapolation is unverified and indeed is
  unverifiable it may or may not be true. The
  physics is hypothetical rather than tested
• Known Physics ? Multiverse ??
  
• NO!
• Known Physics ? Hypothetical Physics ?
  Multiverse
• Major Extrapolation
• It is a great extrapolation from known physics.
• This extrapolation is untestable it may or may
  not be correct.

21

• ?? Implied by inflation, which is justified by
  CBR anisotropy observations
• it is implied by some forms of inflation but not
  others inflation is not yet a well defined
  theory (and not a single scalar field has yet
  been physically detected). Not all forms of
  inflation lead to chaotic inflation.
• For example inflation in small closed universes

22

• However
• Chaotic inflation version can be disproved
  if we observe a small universe have already seen
  round the universe. Therefore spatially closed
• Can search for identical circles in the CBR sky,
  also CMB low anisotropy power at large angular
  scales (which is what is observed).
• A very important test as it would indeed disprove
  the chaotic inflation variety of multiverse.
• - But not seeing them would not prove a
  multiverse exists. Their non-existence is a
  necessary but not sufficient condition .

23

• ?? Implied by probability argument the universe
  is no more special than need be to create life.
• Hence the observed value of the Cosmological
  constant is confirmation (Weinberg).
• But the statistical argument only applies if a
  multiverse exists it is simply inapplicable if
  there is no multiverse.
• In that case we only have one object we can
  observe we can do many observations of that one
  object, but it is still only one object (one
  universe), and you cant do statistical tests if
  there is only one existent entity
• We dont know the measure to use but the result
  depends critically on it
• This is in fact a weak consistency test on
  multiverses, that is indicative but not
  conclusive (a probability argument cannot be
  falsified). Consistency tests must be satisfied,
  but they are not confirmation unless no other
  explanation is possible. Necessary is not
  sufficient.

24

• Implication of all the above
• The multiverse idea is not provable either by
  observation, or as an implication of well
  established physics. It may be true, but cannot
  be shown to be true by observation or experiment.
  
• However it does have great explanatory power it
  does provide an empirically based rationalization
  for fine tuning, developing from known physical
  principles.
• Here one must distinguish between explanation and
  prediction. Successful scientific theories make
  predictions, which can then be tested.
• The multiverse theory cant make any predictions
  because it can explain anything at all.
• Any theory that is so flexible is not testable
  because almost any observation can be
  accommodated.

25

• The key issue is if we choose to let theory trump
  observations, or insist on observational test of
  our theories.
• Multiverse proponents essentially propose the
  former. Scientific conservatism chooses the
  latter.
• The very nature of the scientific enterprise is
  at stake in the multiverse debate
• the multiverse proponents are proposing weakening
  the nature of scientific proof in order to claim
  that multiverses provide a scientific
  explanation.
• This is a dangerous tactic, as is proven by
  history.
• Note we are concerned with really existing
  multiverses, not potential or hypothetical.

26
4 Inhomogeneity and the Acceleration of the
universe

• . The deduction of the existence of dark energy
  is based on the assumption that the universe has
  a Robertson-Walker geometry
• - spatially homogeneous and isotropic on a large
  scale.
• The observations can at least in principle be
  accounted for without the presence of any dark
  energy, if we consider the possibility of
  inhomogeneity
• We abandon the Cosmological Principle that the
  universe is the same everywhere

27
LTB (Lemaitre-Tolman Bondi models

• Metric In comoving coordinates,
• ds2 -dt2 B2(r,t) A2(r,t)(dT2sin2 T dF2)
• where
• B2(r,t) A(r,t)2 (1-k(r))-1
• and the evolution equation is
• (Å/A)2 F(r)/A3 8pG??/3 - k(r)/A2
• with F (AA2)-1 8pG?M.
• Two arbitrary functions k(r) (curvature) and
  F(r) (matter).

28
We can fit the supernova data thats a theorem!
Mustapha, Hellaby, Ellis
29

• Other observations??
• Can also fit cbr observations
• Larger values of r
• S. Alexander, T. Biswas, A. Notari, D. Vaid
  Local void vs dark energy confrontation with
  WMAP and Type IA supernovae (2007)
  arXiv0712.0370.
• Nb cbr dipole can then (partly) be because we
  are a bit off-centre
• Re-evaluate the great attractor analysis
• Quadrupole? Perhaps also (and alignment)
• Nucleosynthesis OK
• Baryon acoustic oscillations?
• Maybe more tricky

30
scales probed by different observations
different distances
The Tegmark representation of power spectrum data
(2006)
31
We find that such a model can easily explain the
observed luminosity distance-redshift relation
of supernovae without the need for dark energy,
when the inhomogeneity is in the form of an
underdense bubble centered near the observer.
With the additional assumption that the universe
outside the bubble is approximately described by
a homogeneous Einstein-de Sitter model, we find
that the position of the first CMB peak can be
made to match the WMAP observations.
32

• Typical observationally viable model
• We live roughly centrally (within 10 of the
  central position) in a large void
• a compensated underdense region stretching to z
  0.08 with d -0.4 and size 160/h Mpc to 250/h
  Mpc, a jump in the Hubble constant of about 1.20,
  and no dark energy or quintessence field
• Solving inverse problem with inhomogenoeus
  universe

33
Large scale inhomogeneitydynamic evolution

• Can we find dynamics (inflation, HBB) that
  matches the observations?
• Same basic dynamics (FRW evolution along
  individual world lines) but with distant
  dependent parameters
• Depends on the initial data, the amount of
  inflation, and the details of the unknown
  inflaton
• If we are allowed usual possibilities of
  arbitrarily choosing the potential, adding in
  multiple fields as needed, and fine-tuning
  initial conditions, then of course we can!

34
Improbability

• It is improbable we are near the centre
• But there is always improbability in cosmology
• Can shift it
• FRW geometry
• Inflationary potential
• Inflationary initial conditions
• Position in inhomogeneous universe
• Which universe in multiverse
• Competing with probability 10-120 for ? in a FRW
  universe.
• Also there is no proof universe is probable.
• May be improbable!! Indeed, it is!!

35

• Do We Live in the Center of the World?
• Andrei Linde, Dmitri Linde, Arthur Mezhlumian
• We investigate the distribution of energy
  density in a stationary self-reproducing
  inflationary universe. We show that the main
  fraction of volume of the universe in a state
  with a given density ? at any given moment of
  time t in synchronous coordinates is concentrated
  near the centers of deep exponentially wide
  spherically symmetric holes in the density
  distribution.
• A possible interpretation of this result is that
  a typical observer should see himself living in
  the center of the world. Validity of this
  interpretation depends on the choice of measure
  in quantum cosmology.
• Phys.Lett.B345203-210,1995
• arXivhep-th/9411111

36
Improbability

• There is only one universe
• Concept of probability does not apply to a single
  object, even though we can make many measurements
  of that single object
• There is no physically realised ensemble to apply
  that probability to, unless a multiverse exists
• which is not proven its a philosophical
  assumption
• and in any case there is no well-justified
  measure for any such probability proposal
• Can we observationally test the inhomogeneity
  possibility?
• Whatever theory may say, it must give way to such
  tests

37
5 Direct Observational tests

• We have stalemate
• DE in FLRW can explain, so can LTB with no DE
• How to discriminate?
• It follows that
• direct observational tests of the Copernican
  (spatial homogeneity) assumption are of
  considerable importance
• particularly those that are independent of field
  equations or matter content

38
Observational Tests

• only previously known direct tests use scattered
  CMB photons - looking inside past null cone
• if CMB very anisotropic around distant observers,
  SZ scattered photons have distorted spectrum
• but model dependent - good for void models but
  misses, e.g., conformally stationary spacetimes
• ideally we need a model-independent forensic
  test ... is FLRW the correct metric?

Goodman 1995 Caldwell Stebbins 2007
39
1 Consistency test of LTB

• Must not have observational cusp at origin
  implies singularity there
• Vanderveld, Flangan and Wasserman
  astro-ph/0602476
• Living in a void Testing the Copernican
  Principle with distant supernovae, T Clifton, P
  G Ferreira and K Land
• Phys. Rev. Lett. 101 (2008) 131302
  arXiv0807.1443
• Distance modulus ?dm(z) - (5/2)q0z in ?CDM, but
  if this were true in void model without ? this
  implies singularity
• - Observational test will be available from
  intermediate redshift supernovae in future

40
Distance Measurements

• two effects on distance measurements

expansion
curvature bends null geodesics

• eg, positive curvature increases angular sizes
• These are coupled in FLRW, decoupled in LTB

41
Measuring Curvature in FLRW

• in FLRW we can combine Hubble rate and distance
  data to find curvature
• independent of all other cosmological parameters,
  including dark energy model, and theory of
  gravity
• can be used at single redshift
• what else can we learn from this?

42
2 Generic Consistency Test of FLRW

• since independent of z we can differentiate
  to get consistency relation
• depends only on FLRW geometry
• independent of curvature, dark energy, theory of
  gravity
• consistency test for homogeneity and isotropy
• should expect in FLRW

A general test of the Copernican Principle Chris
Clarkson, Bruce A. Bassett and Teresa Hui-Ching
Lu Phys.Rev.Lett.101011301,2008
arXiv0712.3457
43
Testing the Copernican Assumption

• Copernican assumption hard to test ... but in
  non-FLRW
• even at center of symmetry
• simplest to measure H(z) from BAO

deceleration parameter measured from distance
measurements
deceleration parameter measured from Hubble
measurements
44
Its only as difficult as dark energy...

• measuring w(z) from Hubble uses
• requires H(z)
• and from distances requires second derivatives
  D(z)
• simplest to begin with
  via

see Clarkson Cortes Bassett JCAP08(2007)011
arXivastro-ph/0702670
45
3 Indirect Observational tests

• If the standard inverse analysis of the supernova
  data to determine the required equation of state
  shows
• there is any redshift range where
• w p/? lt -1,
• this may well be a strong indication that one of
  these geometric explanations is preferable to the
  Copernican (Robertson-Walker) assumption,
• for otherwise the matter model indicated by these
  observations is non-physical (it has a negative
  k.e.)
• M.P. Lima, S. Vitenti, M.J. Reboucas Energy
  conditions bounds and their confrontation with
  supernovae data (2008) arXiv0802.0706.

46

• The physically most conservative approach is to
  assume no unusual dark energy but rather that
  geometry might be responsible for the observed
  apparent acceleration
• This could happen due to large scale
  inhomogeneity that can probably do the job, but
  may not exist
• Observational tests of the latter possibility is
  as important as pursuing the dark energy (exotic
  physics) option in a homogeneous universe
• Theoretical prejudices as to the universes
  geometry, and our place in it, must bow to
  observational tests

47
6 Key Observational tests

• Consistency tests of the standard model
• CBR temperature with z
• T 2.75 (1z)
• Ages, including for objects at high redshift
• T0(object) T(observed) - T(lookback)
• Compare with physical age estimates
• Confirming that helium abundances as a function
  of z are consistent with a primordial value of
  25 at large distances (high redshifts) in all
  directions. This probes very early times at large
  comoving distance

48

• Expand the spatial distances to see the causal
  structure (light cones at 45o)

He4 at early times
49
Key Observational tests

• Consistency tests continued
• Number anisotropy Checking that there is a 2
  number count dipole parallel to the CBR
  independent of source nature and evolution
• G Ellis and J Baldwin,
• MNRAS 206, 377-381 (1984).
• Realistic equation of state not w lt -1
• Test inhomogeneous modes (LTB) on large scale
  Clarkson Bassett and Lu
• Test anisotropic (Bianchi) modes, by CBR
  anisotropy and He4 (talk by Andrew Pontzen)

50
Key Observational tests

• Alternative Global topology
• Closed or not? k 1 ??
• simply connected or not?
• ? Small universe?
• Have we seen right round the universe already,
  maybe many times?
• Identified images
• Number counts
• Circles in the CBR sky
• - Completely different status philosophically

51
7 Status of Testing in cosmology

• Dennis Sciama was always adventurous in both
  physical and geometric speculation
• But
• He insisted on the fundamental importance of the
  relation between theory and observations
• He always insisted on working out testable
  consequences, and then seeing if the test could
  actually be done
• This remains good advice today

52
Status of Untestable models?

• Multiverse claims
• Unobservable universe domains,
• Untested claimed physics
• Theory takes precedence over observations
• Reasonable philosophical proposal.
• Not proven science.
• Universe is a computer simulation
• How could this function?
• Where is this computer?
• How did it come to be there?
• What tests are possible of this claim?
• Neither sensible nor science!

53
Testing the standard model

• Critical tests of the geometry and topology of
  the standard model can be carried out. These will
  either confirm the standard picture in a
  satisfactory way, or will show that one of its
  underlying assumptions is incorrect, and so will
  imply the need for a major revision of the
  consensus model.
• I urge the importance of carrying out these
  critical tests. We need to test the foundations
  of standard cosmology in all possible ways
• Dont just take them for granted!

54
(No Transcript)
55

• Can be disproved if we determine there are
  closed spatial sections because curvature is
  positive k 1
• The claim is that only negatively curved FRW
  models can emerge in a chaotic inflation
  multiverse.
• a because Coleman-de Luccia tunneling only gives
  k -1
• But that claim is already disputed, there are
  already papers suggesting k1 tunneling is
  possible
• - indeed it depends on a very specific
  speculative mechanism, which has not been
  verified to actually work, and indeed such
  verification is impossible.
• b because the spatial sections are then
  necessarily closed and are all that is, if they
  extend far enough
• but we could live in high density lump imbedded
  in a low density universe the extrapolation of
  k1 may not be valid
• Neither
  conclusive!

56

• ?? It is the only physical explanation for fine
  tuning of parameters that lead to our existence,
• in particular the value of the cosmological
  constant
• n.b. theoretical explanation, not observation
• ?? It results from the theory that everything
  that can happen, happens (Lewis, Sciama,
  Deutsch) as suggested by Feynman QFT approach
• n.b. theoretical explanation, not observation
• Which is more important in cosmology
• theory (explanation) or observations (tests
  against reality) ?

57
The Acceleration of the universe

• . The deduction of the existence of dark energy
  is based on the assumption that the universe has
  a Robertson-Walker geometry
• - spatially homogeneous and isotropic on a large
  scale.
• The observations can at least in principle be
  accounted for without the presence of any dark
  energy, if we consider the possibility of
  inhomogeneity
• This can happen in two ways
• local and large scale

58
1 Local inhomogeneitydescription

• Multiple scales of representation
• Implicit averaging scale

Density
Distance
59
Local inhomogeneitydynamic effects

• Averaging and calculating the field equations do
  not commute
• G. F. R. Ellis Relativistic cosmology its
  nature, aims and problems". In General Relativity
  and Gravitation, Ed B Bertotti et al (Reidel,
  1984), 215.
• Large scale effective equations include
  polarisation terms, as in the case of
  electromagnetism
• P Szekeres Linearised gravitational theory in
  macroscopic media
• Ann Phys 64 599 (1971)

60
Local inhomogeneitydynamic effects

• Averaging and calculating the field equations
• do not commute
• g1ab R1ab G1ab T1ab
  Scale 1
• Averaging
• g3ab R3ab G3ab T3ab
  Scale 3
• averaging process
• averaging gives different answer

61
Local inhomogeneitythe averaging problem

• Problem covariant averaging of tensors,
  particularly metric
• Zalaletdinov approach using bitensors
• R Zalaletdinov The Averaging Problem in
  Cosmology and Macroscopic Gravity Int. J. Mod.
  Phys. A 23 1173 (2008) arXiv0801.3256
• Buchert equations for scalars gives modified
  Friedmann equation
• T Buchert Dark energy from structure a status
  report. GRG Journal 40 467 (2008)
  arXiv0707.2153.
• Keypoint
• Expansion and averaging do not commute
• in any domain D, for any field ?
• ?tlt?gt - lt?t?gt lt??gt - lt?gtlt?gt

62
Buchert equations The Raychaudhuri equation
for irrotational dust?tT ? - 4pG? (1/3)T2 -
2s2averages to give ?tltTgtD ? - 4pGlt?gtD
(2/3) lt (T - ltTgtD)2 gtD (1/3)ltTgtD2 2 lt s2 gtD
with correlations acting as a kinetic
pressure.The Friedmann equation
becomes3(åD/aD)2 - 8pGlt?gtD - ? - ltRgtD/2
QD/2where ltRgtD is the averaged curvature and
QD (2/3) lt (T - ltTgtD)2 gtD 2 lt s2 gtD is the
kinematical backreaction term resulting from
expansion and shear fluctuations,

63
Local inhomogeneitydynamic effects

• Claim weak field approximation is adequate and
  shows effect is negligible (Peebles)
• Counter claim as there are major voids in the
  expanding universe a weak-field kind of
  approximation is not adequate
• You have to model (quasi-static) voids and
  junction to expanding external universe
• D.L. Wiltshire "Cosmic clocks, cosmic variance
  and cosmic averages" New J. Phys. 9, 377 (2007)
  arXivgr-qc/0702082.

64
Local inhomogeneitydynamic effects

• Fully explain it? Maybe
• B.M. Leith, S.C.C. Ng and D.L. Wiltshire
• "Gravitational energy as dark energy Concordance
  of cosmological tests" Astrophys. J. 672, L91
  (2008) arXiv07092535.
• T. Mattsson Dark energy as a mirage (2007)
  arXiv0711.4264
• But others disagree
• S. Rasanen Evaluating backreaction with the
  peak model of structure formation
  arxiv0801.2692 (2008).
• But then it still can alter basic relations
  density to curvature

65
2 Local inhomogeneityobservational effects

• Ricci focusing and Weyl focusing
• B. Bertotti The Luminosity of Distant Galaxies
  Proc Royal Soc London. A294, 195 (1966).
• d?/dv -RabKaKb - 2s2 ?2
• dsmn/dv - Emn
• T expansion
• s shear
• Rab Ricci tensor, determined pointwise by
  matter
• Eab Weyl tensor, determined non-locally by
  matter

66

• Robertson-Walker observations
• zero Weyl tensor and non-zero Ricci tensor.
• d?/dv -RabKaKb ?2
• dsmn/dv 0
• Actual observations are best described by zero
  Ricci tensor and non-zero Weyl tensor
• d?/dv - 2s2 ?2
• dsmn/dv - Emn
• This averages out to FRW equations when averaged
  over whole sky
• But supernova observations are preferentially
  where there is no matter

67
Local inhomogeneityobservational effects

• Dyer-Roeder equations are most used to represent
  this
• do not accurately do so no shear, only represent
  reduced density along the bundle of null rays
• C. C Dyer. R C Roeder, Observations in Locally
  Inhomogeneous Cosmological Models Astrophysical
  Journal, Vol. 189 167 (1974)

68
Local inhomogeneityobservational effects

• Determination of Om made by applying the
  homogeneous distance-redshift relation to SN
  1997ap at z0.83 could be as much as 50 lower
  than its true value
• R. Kantowski The Effects of Inhomogeneities on
  Evaluating the mass parameter Om and the
  cosmological constant ? (1998)
  astro-ph/9802208
• Swiss-Cheese models
• FRW regions joined to vacuum regions
• Exact inhomogeneous solutions
• V. Marra, E. W. Kolb, S. Matarrese Light-cone
  averages in a Swiss-Cheese universe (2007)
  arXiv0710.5505.
• Debatable if enough to account for apparent
  acceleration included in Wiltshire papers
• Probably enough to significantly influence
  conconcordance model values