Inf - PowerPoint PPT Presentation
1 / 57
Title:
Inf
Description:
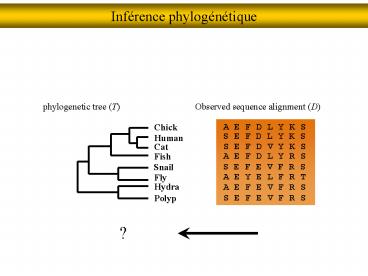
Inf rence phylog n tique Observed sequence alignment (D) phylogenetic tree (T) Chick A E F D L Y K S S E F D L Y K S Human S E F D V Y K S Cat Fish – PowerPoint PPT presentation
Number of Views:89
Avg rating:3.0/5.0
Title: Inf
1
Inférence phylogénétique
Observed sequence alignment (D)
phylogenetic tree (T)
Chick
A E F D L Y K S
S E F D L Y K S
Human
Cat
S E F D V Y K S
Fish
A E F D L Y R S
Snail
S E F E V F R S
A E Y E L F R T
Fly
Hydra
A E F E V F R S
Polyp
S E F E V F R S
?
2
Principes généraux d'une méthode d'inférence
phylogénétique
Deux aspects indépendants à considérer
- Le critère Se définir un score S(T,D) permettant
de mesurer le 'fit' d'un arbre T, sachant les
données D (séquences alignées)
- La méthode de recherche Choisir parmi tous les
arbres possibles de celui ayant le meilleur score
3
Critère 1 Maximum de parcimonie
Pour un arbre donné, le score est le nombre
minimal de changements nécessaires pour expliquer
lalignement
Observed sequence alignment (D)
phylogenetic tree (T)
Chick
A E F D L Y K S
S E F D L Y K S
Human
Cat
S E F D V Y K S
Fish
A E F D L Y R S
Snail
S E F E V F R S
A E Y E L F R T
Fly
Hydra
A E F E V F R S
Polyp
S E F E V F R S
4
Critère 1 Maximum de parcimonie
Pour un arbre donné, le score est le nombre
minimal de changements nécessaires pour expliquer
lalignement
Observed sequence alignment (D)
phylogenetic tree (T)
Chick
A E F D L Y K S
S E F D L Y K S
Human
E
D
Cat
S E F D V Y K S
Fish
A E F D L Y R S
Snail
S E F E V F R S
E
A E Y E L F R T
Fly
Hydra
A E F E V F R S
Polyp
S E F E V F R S
5
Critère 1 Maximum de parcimonie
Pour un arbre donné, le score est le nombre
minimal de changements nécessaires pour expliquer
lalignement
Observed sequence alignment (D)
phylogenetic tree (T)
Chick
A E F D L Y K S
S E F D L Y K S
Human
Cat
S E F D V Y K S
Fish
A E F D L Y R S
Snail
S E F E V F R S
A E Y E L F R T
Fly
Hydra
A E F E V F R S
Polyp
S E F E V F R S
6
Critère 1 Maximum de parcimonie
Pour un arbre donné, le score est le nombre
minimal de changements nécessaires pour expliquer
lalignement
Observed sequence alignment (D)
phylogenetic tree (T)
Chick
A E F D L Y K S
S E F D L Y K S
Human
V
L
V
L
Cat
S E F D V Y K S
Fish
A E F D L Y R S
Snail
S E F E V F R S
L
V
V
A E Y E L F R T
Fly
Hydra
A E F E V F R S
Polyp
S E F E V F R S
Une convergence deux évolutions indépendantes
vers L Une réversion chez le chat, un retour à
l'état ancestral (V) Convergences et réversions
homoplasies
7
Critère 1 Maximum de parcimonie
Pour un arbre donné, le score est le nombre
minimal de changements nécessaires pour expliquer
lalignement
Observed sequence alignment (D)
phylogenetic tree (T)
Chick
A E F D L Y K S
S E F D L Y K S
Human
L
V
Cat
S E F D V Y K S
Fish
A E F D L Y R S
L
V
Snail
S E F E V F R S
L
A E Y E L F R T
Fly
L
V
Hydra
A E F E V F R S
Polyp
S E F E V F R S
8
Maximum de parcimonie
Deux étapes de minimisation
- Pour un arbre donné, minimisation du nombre de
changements nécessaires pour expliquer
lalignement
- Choix parmi tous les arbres possibles de celui
ayant le plus petit nombre de changements
9
méthode naïve
Trouver l'arbre de Maximum de parcimonie
- prendre chaque arbre l'un après l'autre
- pour chaque arbre, calculer le score de
parcimonie - conserver le (ou les) meilleurs arbres
10
méthode naïve
Trouver l'arbre de Maximum de parcimonie
- prendre chaque arbre l'un après l'autre
- pour chaque arbre, calculer le score de
parcimonie - conserver le (ou les) meilleurs arbres
- problème combinatoire trop élevée
11
Heuristiques de recherche de topologies
Agglomération progressive des espèces
- Insertion sur toutes les branches
- Calcul du nombre de changements
- Choix de larbre le plus parcimonieux
Nombre dopérations 35715 (pour 105 arbres
possibles) Pour 10 espèces 63 versus 2 millions
12
Ordre dagglomération des espèces
- Ajouter les espèces de manière aléatoire
- Répéter lopération un grand nombre de fois
- Choisir larbre le plus parcimonieux
13
Algorithme de réarrangements
Réarrangement local ou Nearest Neighbor
Interchange (NNI)
14
Minimums locaux les ilôts darbres optimaux
RÉPLICATS DADDITION ALÉATOIRE DE SEQUENCES
SUCCÈS
ÉCHEC
ÉCHEC
Branch
Swapping
Branch Swapping
Branch Swapping
Longueur De Larbre
Minimum Local
Minimums Locaux
MINIMUM GLOBAL
http//bioinf.ncl.ac.uk/molsys/data/characters.ppt
15
The branch and bound algorithm
Hendy et Penny (1982) Mathematical Biosciences,
60133-142, 1982
16
Utilisation de contraintes a priori
G2
G4
G3
G1
G5
G11
G9
G10
G8
G6
11 espèces 24 106 45 espèces 5 1064
G7
17
Méthode de distances
- Pour chaque paire despèces, calculer la distance
évolutive (cest-à-dire le nombre de différences)
- Choix parmi tous les arbres possibles de celui
correspondant à la matrice de distances - Le critère ici est l'adéquation entre l'arbre et
la matrice de distance
18
Cas idéal
Espèce 1 CUAAAAAAAAA Espèce 2
-AGG------- Espèce 3 AA------UGC Espèce 4
AA--GGCU--C
E1 E2 E3 E4 Espèce 1 0 Espèce 2 3 0 Espèce
3 5 6 0 Espèce 4 7 8 6 0
19
Cas idéal
AAAAAAAAAAA
1
1
CAAAAAAAAAA
AAAAAAAAAAC
2
1
2
4
CUAAAAAAAAA
CAGGAAAAAAA
AAAAAAAAUGC
AAAAGGCUAAC
Espèce 3
Espèce 4
Espèce 1
Espèce 2
Espèce 1 CUAAAAAAAAA Espèce 2
-AGG------- Espèce 3 AA------UGC Espèce 4
AA--GGCU--C
E1 E2 E3 E4 Espèce 1 0 Espèce 2 3 0 Espèce
3 5 6 0 Espèce 4 7 8 6 0
20
Principe des méthodes de distance
E1 E2 E3 E4 Espèce 1 0 Espèce 2 3 0 Espèce
3 5 6 0 Espèce 4 7 8 6 0
Arbre 1
D(E1,E2) ab3 (1) D(E1,E3)
aec5 (2) D(E1,E4) aed7 (3) D(E2,E3)
bec6 (4) D(E2,E4) bed8 (5) D(E3,E4)
cd6 (6)
Plus déquations que de variables en général,
pas de solutions
(2)(4)-(1) ? 2e2c56-3 ? ec4 (7) (2)(7) ?
a5-41 (1) ? b3-12 (4)(5)(6) ? 2b2e68-6
? be4 ? e4-22 (4) ? c6-2-22 (5) ?
d8-2-24
21
Principe des méthodes de distance
E1 E2 E3 E4 Espèce 1 0 Espèce 2 3 0 Espèce
3 5 6 0 Espèce 4 7 8 6 0
Arbre 2
D(E1,E2) aeb3 (1) D(E1,E3)
ac5 (2) D(E1,E4) aed7 (3) D(E2,E3)
bec6 (4) D(E2,E4) bd8 (5) D(E3,E4)
ced6 (6)
Plus déquations que de variables en général,
pas de solutions
(2)(4)-(1) ? 2c56-3 ? c4 (2) ? a5-41 ?
a1 (3)(4)-(5) ? ac2e76-85 ? e0 (1) ?
b3-12 ? b2 (5) ? d8-26 ? d6 (6) ?
4066 ?106
22
Distances additives et ultramétriques
Une matrice de distances est dite additive
(darbre) si et seulement il existe un arbre
ayant des longueurs de branches parfaitement
compatibles avec la matrice Conditions des 4
points Pour tout ensemble de 4 espèces i,j,k et
l, deux des valeurs D(i,j)D(k,l), D(i,k)D(j,l)
et D(i,l)D(j,k) sont égales et supérieures à la
troisième
23
Une substitution multiple
Substitutions multiples entraînent une
sous-estimation des distances
E1 E2 E3 E4 Espèce 1 0 Espèce 2 3 0 Espèce 3 4
(5) 5 (6) 0 Espèce 4 7 8 6 0
Distances non additives
24
Moindres carrés
Appelons P une distance correspondant à un arbre
phylogénétique T ? les espèces i et j, P(i,j)
Sarètes sur le chemin connectant i et j
Soit F la fonction qui mesure la qualité de
lajustement (fit) de P à D
ou
- On calcule les arètes de longueur inconnue (a,
b, c, d et e, dans le cas précédent) en
minimisant F par une méthode de moindre carré
(least square method) - On choisit parmi tous les arbres possibles celui
qui minimise F
Comme en parcimonie, deux étapes
dajustement/minimisation
25
Algorithme du Neighbor Joining (SaitouNei, 1987)
26
Une substitution multiple
E1 E2 E3 E4 Espèce 1 0 Espèce 2 3 0 Espèce 3 4
(5) 5 (6) 0 Espèce 4 7 8 6 0
27
Trois substitutions multiples
E1 E2 E3 E4 Espèce 1 0 Espèce 2 3 0 Espèce 3 3
(5) 1 (6) 0 Espèce 4 7 7 (8) 6 0
1.8
0.6
E1
E2
0.7
E4
E3
5.2
0.4
Nécessité de corriger les distances avant
dinférer larbre
28
Calcul de la distance évolutive
Mutation altération dune molécule dADN
(mutation ponctuelle si un seul nucléotide est
modifié)
Substitution modification de la séquence dADN
dans lensemble de la population
Distance évolutive nombre de substitutions
ayant eu lieu entre deux espèces (ou organismes)
PRINCIPE estimer à partir des différences
observées entre deux séquences le nombre de
substitutions qui se sont produites
? Nécessité dun modèle dévolution des séquences
29
A simple model Jukes and Cantor
Evolution operates independently and identically
at each position
A A C A G T A C
Markov process - no memory - time-homogeneous
- of rate ?
G C
A A C A C T A C
C A
For each substitution, draw final state with
equal probability (1/3)
A G
A G C A A T A C
time
30
Modèle de Jukes et Cantor (1969)
- Toutes les substitutions sont équiprobables (par
exemple si A est modifié, il y a une chance sur
trois que ce soit en C, 1/3 en G et 1/3 en T) - Tous les sites ont la même probabilité de subir
une substitution
Soit l la fréquence de substitutions par million
d'années Soit qt la fréquence des nucléotides
identiques entre la séquence à linstant t et la
séquence à linstant 0
On cherche à calculer qt1 la fréquence des
nucléotides identiques entre la séquence à
linstant t 1 et la séquence à linstant 0
qt1
(1-l)qt sites qui restent constants
31
Modèle de Jukes et Cantor (1969)
- Toutes les substitutions sont équiprobables (par
exemple si A est modifié, il y a une chance sur
trois que ce soit en C, 1/3 en G et 1/3 en T) - Tous les sites ont la même probabilité de subir
une substitution
D distance évolutive (nombre de
substitutions) Q p-distance (nombre de
différences observées)
32
Modèle de Jukes et Cantor (1969)
1
0.9
0.75
0.8
0.7
0.6
0.5
p-distance (différences observées)
0.4
0.3
0.2
0.1
0
0
1
2
3
4
5
6
DJC (substitutions estimées)
33
Modèle de Kimura (1980)
- Transition remplacement dune purine (A et G)
par une autre ou dune pyrimidine (C et T) par
une autre. - Transversion remplacement dune purine (A et G)
par une pyrimidine (C et T).
34
Modèle de Kimura (1980)
- Transition remplacement dune purine (A et G)
par une autre ou dune pyrimidine (C et T) par
une autre. - Transversion remplacement dune purine (A et G)
par une pyrimidine (C et T).
- Les substitutions sont séparées en deux
catégories transitions et transversions. A
lintérieur de ces deux catégories, les
changements sont équiprobables (même probabilité
de passer de A vers C que de A vers T) - Tous les sites ont la même probabilité de subir
une substitution
35
Modèle de Jukes et Cantor (1969)
1
0.9
0.75
0.8
0.7
(2 nucléotides) 0.50
0.6
0.5
p-distance (différences observées)
0.4
0.3
0.2
0.1
0
0
1
2
3
4
5
6
DJC (substitutions estimées)
36
A simple model Felsenstein 1981
Evolution operates independently and identically
at each position
A A C A G T A C
Markov process - no memory - time-homogeneous
- of rate ?
G C
A A C A C T A C
C A
For each substitution, draw final state from
frequency vector
A G
A G C A A T A C
time
A C G T F G H I K L M N P Q R S T V W Y
37
Modèle de Felsenstein (1981)
- Toutes les substitutions sont équiprobables (par
exemple si A est modifié, il y a une chance sur
trois que ce soit en C, 1/3 en G et 1/3 en T) - Tous les sites ont la même probabilité de subir
une substitution - Les fréquences des quatre nucléotides ne sont pas
obligatoirement 0.25, 0.25, 0.25 et 0.25
38
General Time Reversible (GTR) model
- Chaque type de substitutions nucléotidiques a sa
propre probabilité - Tous les sites ont la même probabilité de subir
une substitution - Les fréquences des quatre nucléotides ne sont pas
obligatoirement 0.25, 0.25, 0.25 et 0.25
39
Variabilité du taux de substitutions entre
positions
Nombre de substitutions par position
Alignement de cytochrome b
2065 séquences de cytochrome b de Vertebrés
40
Variabilité du taux de substitutions entre
positions
Nombre de substitutions par position
Alignement de cytochrome b
41
Modélisation par une distribution G
a paramètre de forme
42
Variabilité du taux de substitutions entre
positions
Nei et Gojobori (1986)
Jin et Nei (1990)
Tamura et Nei (1993)
a, paramètre de la loi G p, P, P1, P2 et Q
fréquences des différences, transitions,transition
s A/G, transitions CXT et transversions,
respectivement f, fréquence des nucléotides
(Rpurines, Ypyrimidines)
43
(No Transcript)
44
Robustesse des phylogénies lindice de Bremer
Indice de Bremer nombre de pas à ajouter à la
longueur de larbre le plus parcimonieux pour
casser la monophylie du clade considéré
Indice de Bremer (Bremer Decay Index) est égal
à Le nombre de pas de larbre le plus
parcimonieux dans lequel le clade considéré nest
pas monophylétique Moins Le nombre de pas de
larbre le plus parcimonieux dans lequel le clade
considéré est monophylétique
45
Robustesse des phylogénies le test du bootstrap
- Tirage avec remise de n positions parmi n
positions - Construire larbre phylogénétique
- Répéter 1) et 2) un grand nombre de fois (1000)
- Analyser tous les arbres obtenus (en particulier
via un arbre consensus)
46
Larbre de consensus majoritaire
Etc.
- On calcule la fréquence dapparition des
différents groupements despèces - E et F 100
- D, E et F 93
- A et B 52
- A et C 48
- C, E et F 7
- Construire larbre consensus
47
Robustesse des phylogénies le test du jackknife
Jackknife tirage sans remise de x des
positions originales
1
1
0
1
1
1
1
0
1
1
1
0
1
0
1
0
1
1
0
1
1
1
1
0
Le but du jackknife est de savoir si une petite
fraction de lalignement a un impact sur
linférence phylogénétique
48
Robustesse des phylogénies le test du bootstrap
Le tirage avec remise de positions, en respectant
leffectif original, revient à conférer un poids
aléatoire aux positions
Par exemple 2 1 0 3 0 2 1 1 1 3 0 4 0 0 1 2 2 1
1 3 0 1 0 1 3 2 0 0 (à chaque tirage, un tiers
des positions ne sont pas considérés)
Le but du bootstrap vise à mesurer si le signal
phylogénétique en faveur d'un groupe donné est
présent dans beaucoup de colonnes de l'alignement
- Problèmes
- Très couteux en temps calcul
- Seuil de significativité (70, 95)
49
Le principe de parcimonie
- Interpretation "Philosophique"
- rasoir d'Occam
- l'économie d'hypothèses est à la base de la
science
Interprétation probabiliste chaque fois que deux
espèces ont un caractère en commun, deux
interprétations sont possibles 1- caractère
hérité de l'ancêtre commun 2- convergence
(acquisition indépendante) Maximum de Parcimonie
ltgt 1 est plus probable que 2
50
Le principe de parcimonie mis en défaut
D'après l'interprétation probabiliste, toutes les
fois où les convergences sont plus probables que
les caractères dérivés partagés, le principe du
Maximum de Parcimonie est inconsistant.
51
Attraction des longues branches
1
4
q
q
2 et4 ont des branches très courtes ont gardé
l'état ancestral 1 et 3 ont des branches très
longues présentent un état complètement
aléatoire ( ¼ A, ¼ C, ¼ G ¼ T)
p
3
2
Felsenstein, 1978
A C G T A C G T A C G T A C G T
A A A A A A A A A A A A A A A A
A A A A C C C C G G G G T T T T
A A A A A A A A A A A A A A A A
A
A
A
52
Attraction des longues branches
1
4
1
4
1
2
3
2
2
3
3
4
Seuls ces trois états sont informatifs (tous les
autres ont meme score de parcimonie sur les 3
arbres possibles)
Felsenstein, 1978
A C G T A C G T A C G T A C G T
A A A A A A A A A A A A A A A A
A A A A C C C C G G G G T T T T
A A A A A A A A A A A A A A A A
A
A
A
53
Attraction des longues branches Le maximum de
parcimonie favorise l'arbre faux
A
C
A
C
q
q
pltq2
p
D
B
D
B
Felsenstein, 1978
54
Attraction des longues branches
A
C
A
C
q
q
pltq2
p
D
B
D
B
Felsenstein, 1978
55
Inconsistence de linférence phylogénétique
Une méthode de reconstruction phylogénétique est
dite inconsistente si elle converge vers un
résultat faux quand il y a de plus en plus de
données
ATTENTION un très bon support statistique (par
ex. 100 de bootstrap) ne garantit pas que le
noeud inféré est correct
56
Echantillonnage taxonomique
Ajouter des espèces à lanalyse permet de mieux
détecter les substitutions multiples
Ajouter des espèces peut casser les longues
branches et ainsi éviter lartefact dattraction
des longues branches (Hendy et Penny, 1989)
57
Biais de composition
Problème les différentes espèces nont pas les
mêmes compositions en bases
Aquifex GC76
Thermus GC73
Deinococcus GC49
Distance Jukes et Cantor
Bacillus GC50
ARN ribosomique 16S