Integration - PowerPoint PPT Presentation
1 / 13
Title:
Integration
Description:
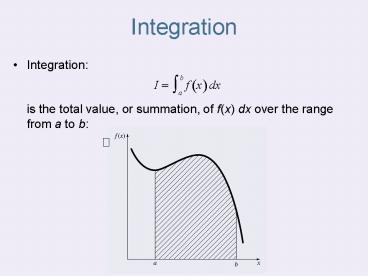
Integration Integration: is the total value, or summation, of f(x) dx over the range from a to b: Composite Trapezoidal Rule Assuming n+1 data points are evenly ... – PowerPoint PPT presentation
Number of Views:217
Avg rating:3.0/5.0
Title: Integration
1
Integration
- Integrationis the total value, or summation,
of f(x) dx over the range from a to b
2
Composite Trapezoidal Rule
- Assuming n1 data points are evenly spaced, there
will be n intervals over which to integrate. - The total integral can be calculated by
integrating each subinterval and then adding them
together
3
Simpsons Rules
- More complicated approximation formulas can
improve the accuracy for curves - these include
using (a) 2nd and (b) 3rd order polynomials. - The formulas that result from taking the
integrals under these polynomials are called
Simpsons rules.
4
Simpsons Rule
- Simpsons rule corresponds to using second-order
polynomials - Integration over the three points simplifies to
5
Composite Simpsons Rule
- Simpsons rule can be used on a set of
subintervals in much the same way the trapezoidal
rule was, except there must be an odd number of
points. - Because of the heavy weighting of the internal
points, the formula is a little more complicated
than for the trapezoidal rule
6
Simpsons 3/8 Rule
- Simpsons 3/8 rule corresponds to using
third-order polynomials to fit four points.
Integration over the four points simplifies
to - Simpsons 3/8 rule is generally used in concert
with Simpsons 1/3 rule when the number of
segments is odd.
7
Integration with Unequal Segments
- Previous formulas were simplified based on
equispaced data points - though this is not
always the case. - The trapezoidal rule may be used with data
containing unequal segments
8
MATLAB Functions
- MATLAB has built-in functions to evaluate
integrals based on the trapezoidal rule - z trapz(y)z trapz(x, y)produces the
integral of y with respect to x. If x is omitted,
the program assumes h1. - z cumtrapz(y)z cumtrapz(x, y)produces the
cumulative integral of y with respect to x. If x
is omitted, the program assumes h1.
9
Example
- Approximate the distance travelled from the
following experimental data - Note, distance travelled is area under curve of
velocity, ie integral
t 0 1 1.4 2 3 4.3 6 6.7 8
v 0 10 13 19 26 34 41 43 46
10
Gauss Quadrature
- Gauss quadrature describes a class of techniques
for evaluating the area under a straight line by
joining any two points on a curve rather than
simply choosing the endpoints. - The key is to choose the line that balances the
positive and negative errors.
11
Gauss-Legendre Formulas
- The Gauss-Legendre formulas seem to optimize
estimates to integrals for functions over
intervals from -1 to 1. - Integrals over other intervals require a change
in variables to set the limits from -1 to 1. - The integral estimates are of the formwhere
the ci and xi are calculated to ensure that the
method exactly integrates up to (2n-1)th order
polynomials over the interval from -1 to 1.
12
Adaptive Quadrature
- Methods such as Simpsons 1/3 rule has a
disadvantage in that it uses equally spaced
points - if a function has regions of abrupt
changes, small steps must be used over the entire
domain to achieve a certain accuracy. - Adaptive quadrature methods for integrating
functions automatically adjust the step size so
that small steps are taken in regions of sharp
variations and larger steps are taken where the
function changes gradually.
13
Adaptive Quadrature in MATLAB
- MATLAB has two built-in functions for
implementing adaptive quadrature - quad uses adaptive Simpson quadrature
- q quad(fun, a, b, tol, trace, p1, p2, )
- fun function to be integrated
- a, b integration bounds
- tol desired absolute tolerance (default 10-6)
- trace flag to display details or not
- p1, p2, extra parameters for fun
- quadl has the same arguments