Beams - PowerPoint PPT Presentation
1 / 26
Title: Beams
1
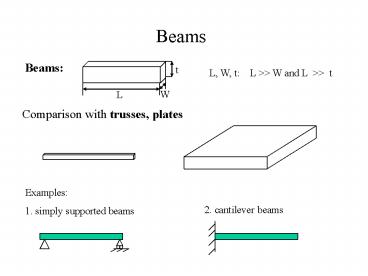
Beams
Beams
t
L, W, t L gtgt W and L gtgt t
W
L
Comparison with trusses, plates
Examples
2. cantilever beams
1. simply supported beams
2
Beams - loads and internal loads
Loads concentrated loads, distributed loads,
couples (moments)
Internal loads shear force and bending moments
3
Shear Forces, Bending Moments - Sign Conventions
right section
left section
Shear forces
positive shear
negative shear
Bending moments
positive moment
negative moment
4
Shear Forces, Bending Moments - Static
Equilibrium Approach
Procedure 1. find reactions 2. cut the beam
at a certain cross section, draw F.B.D. of one
piece of the beam 3. set up equations 4.
solve for shear force and bending moment at that
cross section 5. draw shear and bending moment
diagrams.
Example 1 Find the shear force and bending
diagram at any cross section of the beam shown
below.
5
Relationship between Loads, Shear Forces, and
Bending Diagram
6
Beam - Normal Strain
M
M
no transverse load
Pure bending problem
no axial load
no torque
Observations of the deformed beam under pure
bending
Length of the longitudinal elements
Vertical plane remains plane after deformation
Beam deforms like an arc
7
Normal Strain - Analysis
neutral axis (N.A.)
radius of curvature
Coordinate system
q
longitudinal strain
r
y
N.A.
8
Beam - Normal Stress
Hookes Law
y
M
M
M
x
Maximum stresses
Neutral axis
9
Flexure Formula
y
Moment balance
M
x
Comparison
Axially loaded members
Torsional shafts
10
Moment of Inertia - I
Example 2
h
w
Example 3
h
w
w
4h
w
11
Design of Beams for Bending Stresses
Design Criteria
1.
2. cost as low as possible
Design Question Given the loading and
material, how to choose the shape and the size
of the beam so that the two design criteria are
satisfied?
12
Design of Beams for Bending Stresses
Procedure
- Find Mmax
- Calculate the required section modulus
- Pick a beam with the least cross-sectional area
or weight - Check your answer
13
Design of Beams for Bending Stresses
Example 4 A beam needs to support a uniform
loading with density of 200 lb /ft. The
allowable stress is 16,000 psi. Select the shape
and the size of the beam if the height of the
beam has to be 2 in and only rectangular and
circular shapes are allowed.
6 ft
14
Shear Stresses inside Beams
shear force V
V
Horizontal shear stresses
y
h1
y1
x
h2
s2
s1
tH
15
Shear Stresses inside Beams
Relationship between the horizontal shear
stresses and the vertical shear stresses
y
h1
y1
x
h2
Shear stresses - force balance
V shear force at the transverse cross section Q
first moment of the cross sectional area above
the level at which the shear stress is
being evaluated w width of the beam at the
point at which the shear stress is being
evaluated I second moment of inertial of the
cross section
16
Shear Stresses inside Beams
Example 5 Find shear stresses at points A, O and
B located at cross section a-a.
P
a
A
O
a
B
w
17
Shear Stress Formula - Limitations
- elementary shear stress theory
Assumptions 1. Linearly elastic material,
small deformation 2. The edge of the cross
section must be parallel to y axis, not
applicable for triangular or
semi-circular shape 3. Shear stress must be
uniform across the width 4. For rectangular
shape, w should not be too large
18
Shear Stresses inside Beams
Example 6 The transverse shear V is 6000 N.
Determine the vertical shear stress at the web.
19
Beams - Examples
Example 7 For the beam and loading shown,
determine (1) the largest
normal stress (2) the largest
shearing stress (3) the shearing
stress at point a
20
Deflections of Beam
Deflection curve of the beam deflection of the
neutral axis of the beam.
y
P
y
x
x
Derivation
Moment-curvature relationship
Curvature of the deflection curve
(1)
(2)
Small deflection
(3)
Equations (1), (2) and (3) are totally
equivalent.
21
Deflections by Integration of the Moment
Differential Equation
Example 8 (approach 1)
22
Deflections by Integration of the Load
Differential Equation
Example 8 (approach 2)
23
Method of Superposition
P
q
Deflection y
P
Deflection y2
Deflection y1
24
Method of Superposition
Example 9
25
Statically Indeterminate Beam
Number of unknown reactions is larger than the
number of independent Equilibrium equations.
Propped cantilever beam
Clamped-clamped beam
Continuous beam
26
Statically Indeterminate Beam
Example 10. Find the reactions of the propped
beam shown below.