M - PowerPoint PPT Presentation
Title: M
1
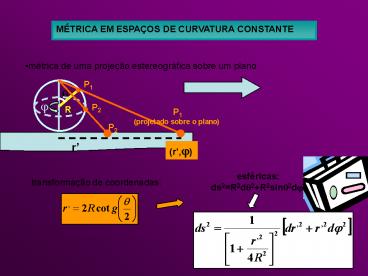
MÉTRICA EM ESPAÇOS DE CURVATURA CONSTANTE
- métrica de uma projeção estereográfica sobre um
plano
P1
esféricas ds2R2d?2R2sin?2d?2
transformação de coordenadas
2
- perímetro de um círculo geodésico
r é fixo ? dr?0
- área de um círculo geodésico
3
Como para uma superfície esférica
métrica de um plano em coordenadas polares
deformação que uma esfera deve sofrer
para tranformar-se num plano ou vice-versa.
4
reescrevendo
x1rcos? x2rsin?
Métrica válida para ? superfície de curvatura
constante de qualquer sinal
Forma generalizada a um no de dimensões n
5
Métricas 3D para espaço de ? constante
x1r sin? cos? x2r sin? sin? x3r cos?
Em coordenadas esféricas
Forma comum da métrica na cosmologia
Nota a não é o raio próprio.
6
Ex. caso 2D
Coordenadas (a,?)
r raio próprio ? medido sobre a superfície
voltando a superfície 3D...
Cálculo do raio próprio
Fixando os ângulos ? e ?
7
APLICAÇÃO HIPER-ESFERA
Definição espaços de curvatura positiva e
constante
com K gt 0 e constante
- raio próprio de
- uma esfera geodésica
- área (de uma esfera de raio a dentro deste
espaço)
8
A área de uma esfera de raio próprio r imersa em
um espaço de ? gt 0 e constante
- r cresce área máxima quando
- quando
9
O volume de uma esfera de raio a dentro de um
espaço
? gt 0 e constante
para uma métrica ortogonal
Vmáx ? volume engloba todo o espaço de ? gt 0 e
constante
volume finito !
espaço de ? gt 0 e constante é finito
mas sem bordas...
10
Entretanto...
Espaço de ? ? 0 e constante são infinitos
Ex. uma esfera de volume V(a) dentro de um
espaço de curvatura negativa
Espaços deste tipo são ditos espaços infinitos
Quando a?8 V(a) ?8
Se ?0 , o volume de uma esfera em um espaço
euclidiano é
Tb quando a?8 V(a) ?8
V(a)(4?/3)a3
11
Espaços Riemannianos
Definição sempre que ds2 for representado por
uma forma diferencial qualdrática ? MÉTRICA
RIEMANNIANA
Ex. para uma superfície
Característica importante métrica riemanniana é
localmente euclidiana !!
12
Demonstração nas viz. De um ponto P0, A0, B0 e
C0 são números
Fazendo
Nas viz. De ? ponto sobre uma superfície Riemannia
na a métrica pode ser aproximada como uma métrica
euclidiana
ds2dx1dx2
13
Através de medidas de ângulos, perímetros ou
áreas sobre uma dada superfície podemos medir a ?
Ir até as galáxias mais distantes e fazer medidas
por triangulação (!!!!??)
14
Número de galáxias num dado volume
Galáxias uniformemente distribuídas aumentando o
raio ? aumenta o no de galáxias
Se raio ? 2?raio
K0 N ? 8N
k1 N lt 8N
k-1 N gt 8N
15
Modelos cosmológicos R(t)